McGAN: Generating Manufacturable Designs by Embedding Manufacturing Rules into Conditional Generative Adversarial Network

Generative design (GD) methods aim to automatically generate a wide variety of designs that satisfy functional or aesthetic design requirements. However, research to date generally lacks considerations of manufacturability of the generated designs. To this end, we propose a novel GD approach by using deep neural networks to encode design for manufacturing (DFM) rules, thereby modifying part designs to make them manufacturable by a given manufacturing process. Specifically, a three-step approach is proposed: first, an instance segmentation method, Mask R-CNN, is used to decompose a part design into subregions. Second, a conditional generative adversarial neural network (cGAN), Pix2Pix, transforms unmanufacturable decomposed subregions into manufacturable subregions. The transformed subregions of designs are subsequently reintegrated into a unified manufacturable design. These three steps, Mask-RCNN, Pix2Pix, and reintegration, form the basis of the proposed Manufacturable conditional GAN (McGAN) framework. Experimental results show that McGAN can transform existing unmanufacturable designs to generate their corresponding manufacturable counterparts automatically that realize the specified manufacturing rules in an efficient and robust manner. The effectiveness of McGAN is demonstrated through two-dimensional design case studies of an injection molding process.

MAC: Maximizing Algebraic Connectivity for Graph Sparsification

Simultaneous localization and mapping (SLAM) is a critical capability in autonomous navigation, but memory and computational limits make long-term application of common SLAM techniques impractical; a robot must be able to determine what information should be retained and what can safely be forgotten. In graph-based SLAM, the number of edges (measurements) in a pose graph determines both the memory requirements of storing a robot's observations and the computational expense of algorithms deployed for performing state estimation using those observations, both of which can grow unbounded during long-term navigation. Motivated by these challenges, we propose a new general purpose approach to sparsify graphs in a manner that maximizes algebraic connectivity, a key spectral property of graphs which has been shown to control the estimation error of pose graph SLAM solutions. Our algorithm, MAC (for maximizing algebraic connectivity), is simple and computationally inexpensive, and admits formal post hoc performance guarantees on the quality of the solution that it provides. In application to the problem of pose-graph SLAM, we show on several benchmark datasets that our approach quickly produces high-quality sparsification results which retain the connectivity of the graph and, in turn, the quality of corresponding SLAM solutions.

Multi-Irreducible Spectral Synchronization for Robust Rotation Averaging

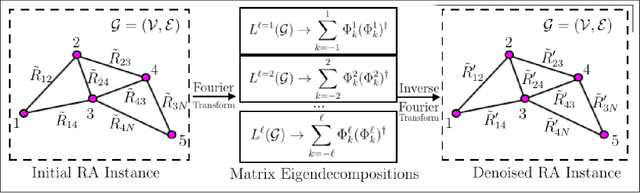
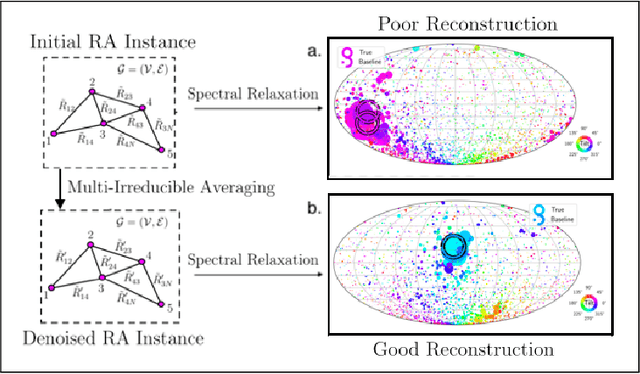
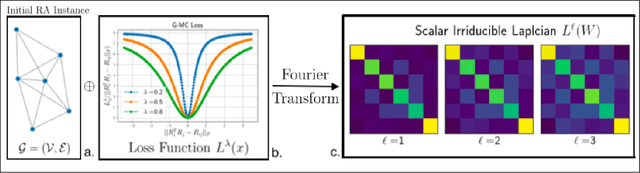
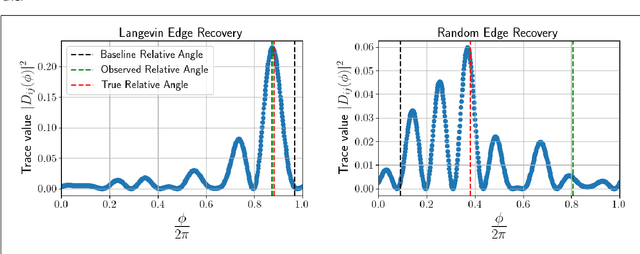
Rotation averaging (RA) is a fundamental problem in robotics and computer vision. In RA, the goal is to estimate a set of $N$ unknown orientations $R_{1}, ..., R_{N} \in SO(3)$, given noisy measurements $R_{ij} \sim R^{-1}_{i} R_{j}$ of a subset of their pairwise relative rotations. This problem is both nonconvex and NP-hard, and thus difficult to solve in the general case. We apply harmonic analysis on compact groups to derive a (convex) spectral relaxation constructed from truncated Fourier decompositions of the individual summands appearing in the RA objective; we then recover an estimate of the RA solution by computing a few extremal eigenpairs of this relaxation, and (approximately) solving a consensus problem. Our approach affords several notable advantages versus prior RA methods: it can be used in conjunction with \emph{any} smooth loss function (including, but not limited to, robust M-estimators), does not require any initialization, and is implemented using only simple (and highly scalable) linear-algebraic computations and parallelizable optimizations over band-limited functions of individual rotational states. Moreover, under the (physically well-motivated) assumption of multiplicative Langevin measurement noise, we derive explicit performance guarantees for our spectral estimator (in the form of probabilistic tail bounds on the estimation error) that are parameterized in terms of graph-theoretic quantities of the underlying measurement network. By concretely linking estimator performance with properties of the underlying measurement graph, our results also indicate how to devise measurement networks that are \emph{guaranteed} to achieve accurate estimation, enabling such downstream tasks as sensor placement, network compression, and active sensing.

Lagrangian Duality in 3D SLAM: Verification Techniques and Optimal Solutions

State-of-the-art techniques for simultaneous localization and mapping (SLAM) employ iterative nonlinear optimization methods to compute an estimate for robot poses. While these techniques often work well in practice, they do not provide guarantees on the quality of the estimate. This paper shows that Lagrangian duality is a powerful tool to assess the quality of a given candidate solution. Our contribution is threefold. First, we discuss a revised formulation of the SLAM inference problem. We show that this formulation is probabilistically grounded and has the advantage of leading to an optimization problem with quadratic objective. The second contribution is the derivation of the corresponding Lagrangian dual problem. The SLAM dual problem is a (convex) semidefinite program, which can be solved reliably and globally by off-the-shelf solvers. The third contribution is to discuss the relation between the original SLAM problem and its dual. We show that from the dual problem, one can evaluate the quality (i.e., the suboptimality gap) of a candidate SLAM solution, and ultimately provide a certificate of optimality. Moreover, when the duality gap is zero, one can compute a guaranteed optimal SLAM solution from the dual problem, circumventing non-convex optimization. We present extensive (real and simulated) experiments supporting our claims and discuss practical relevance and open problems.