COVID-19 case data for Italy stratified by age class

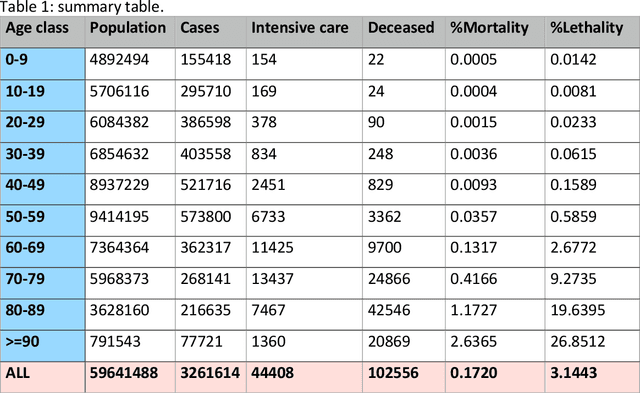
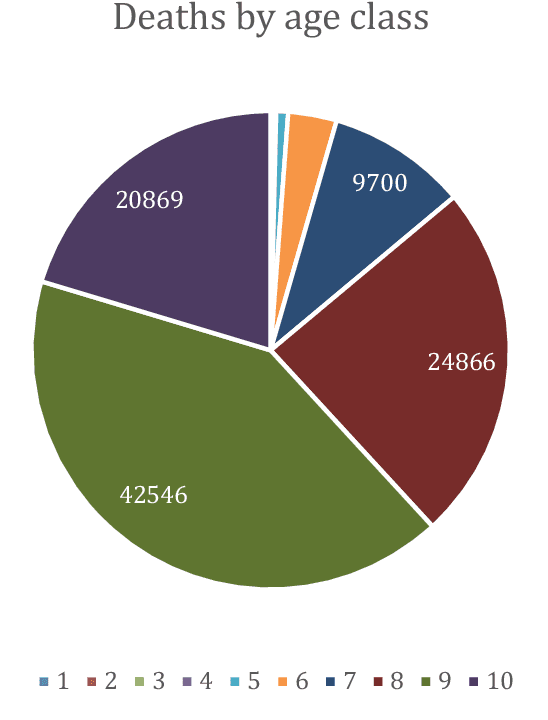
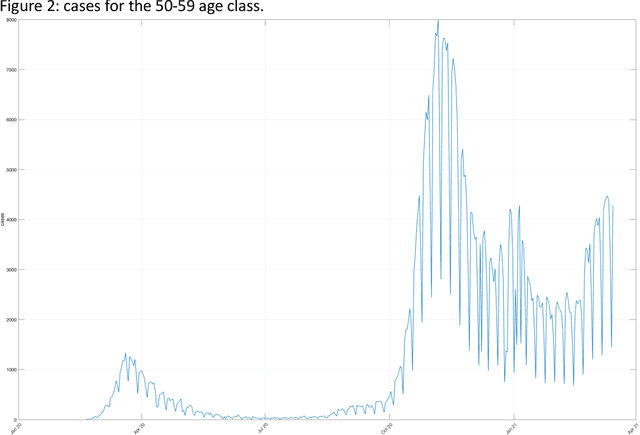
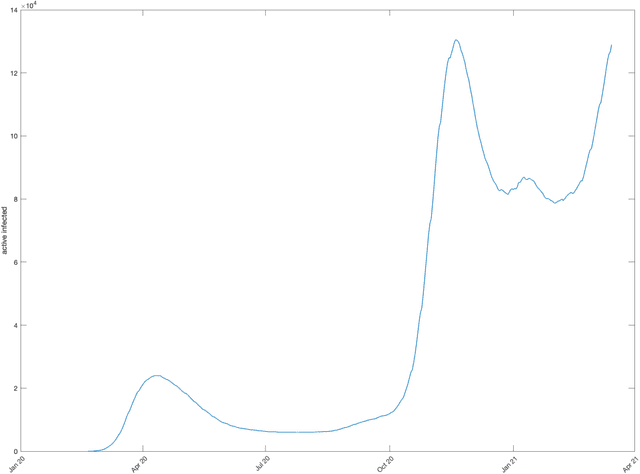
The dataset described in this paper contains daily data about COVID-19 cases that occurred in Italy over the period from Jan. 28, 2020 to March 20, 2021, divided into ten age classes of the population, the first class being 0-9 years, the tenth class being 90 years and over. The dataset contains eight columns, namely: date (day), age class, number of new cases, number of newly hospitalized patients, number of patients entering intensive care, number of deceased patients, number of recovered patients, number of active infected patients. This data has been officially released for research purposes by the Italian authority for COVID-19 epidemiologic surveillance (Istituto Superiore di Sanit\`a - ISS), upon formal request by the authors, in accordance with the Ordonnance of the Chief of the Civil Protection Department n. 691 dated Aug. 4 2020. A separate file contains the numerosity of the population in each age class, according to the National Institute of Statistics (ISTAT) data of the resident population of Italy as of Jan. 2020. This data has potential use, for instance, in epidemiologic studies of the effects of the COVID-19 contagion in Italy, in mortality analysis by age class, and in the development and testing of dynamical models of the contagion.

Lagrangian Duality in 3D SLAM: Verification Techniques and Optimal Solutions

State-of-the-art techniques for simultaneous localization and mapping (SLAM) employ iterative nonlinear optimization methods to compute an estimate for robot poses. While these techniques often work well in practice, they do not provide guarantees on the quality of the estimate. This paper shows that Lagrangian duality is a powerful tool to assess the quality of a given candidate solution. Our contribution is threefold. First, we discuss a revised formulation of the SLAM inference problem. We show that this formulation is probabilistically grounded and has the advantage of leading to an optimization problem with quadratic objective. The second contribution is the derivation of the corresponding Lagrangian dual problem. The SLAM dual problem is a (convex) semidefinite program, which can be solved reliably and globally by off-the-shelf solvers. The third contribution is to discuss the relation between the original SLAM problem and its dual. We show that from the dual problem, one can evaluate the quality (i.e., the suboptimality gap) of a candidate SLAM solution, and ultimately provide a certificate of optimality. Moreover, when the duality gap is zero, one can compute a guaranteed optimal SLAM solution from the dual problem, circumventing non-convex optimization. We present extensive (real and simulated) experiments supporting our claims and discuss practical relevance and open problems.

Pose Graph Optimization in the Complex Domain: Lagrangian Duality, Conditions For Zero Duality Gap, and Optimal Solutions

Pose Graph Optimization (PGO) is the problem of estimating a set of poses from pairwise relative measurements. PGO is a nonconvex problem, and currently no known technique can guarantee the computation of an optimal solution. In this paper, we show that Lagrangian duality allows computing a globally optimal solution, under certain conditions that are satisfied in many practical cases. Our first contribution is to frame the PGO problem in the complex domain. This makes analysis easier and allows drawing connections with the recent literature on unit gain graphs. Exploiting this connection we prove non-trival results about the spectrum of the matrix underlying the problem. The second contribution is to formulate and analyze the dual problem in the complex domain. Our analysis shows that the duality gap is connected to the number of eigenvalues of the penalized pose graph matrix, which arises from the solution of the dual. We prove that if this matrix has a single eigenvalue in zero, then (i) the duality gap is zero, (ii) the primal PGO problem has a unique solution, and (iii) the primal solution can be computed by scaling an eigenvector of the penalized pose graph matrix. The third contribution is algorithmic: we exploit the dual problem and propose an algorithm that computes a guaranteed optimal solution for PGO when the penalized pose graph matrix satisfies the Single Zero Eigenvalue Property (SZEP). We also propose a variant that deals with the case in which the SZEP is not satisfied. The fourth contribution is a numerical analysis. Empirical evidence shows that in the vast majority of cases (100% of the tests under noise regimes of practical robotics applications) the penalized pose graph matrix does satisfy the SZEP, hence our approach allows computing the global optimal solution. Finally, we report simple counterexamples in which the duality gap is nonzero, and discuss open problems.