Haoen Huang
Multi-Irreducible Spectral Synchronization for Robust Rotation Averaging
Nov 28, 2023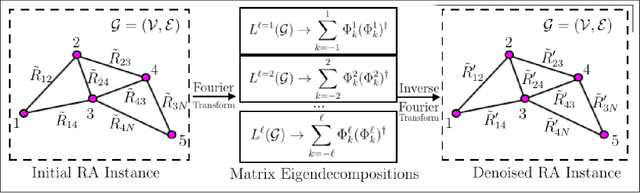
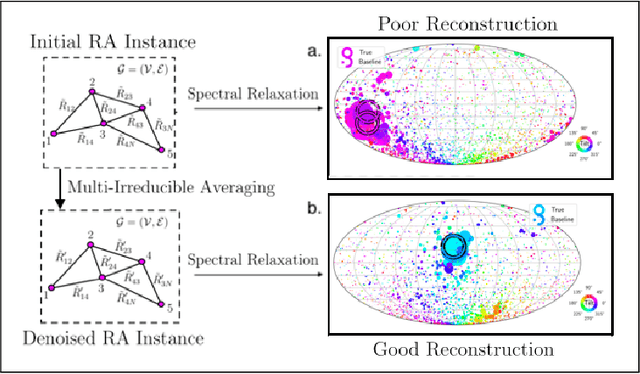
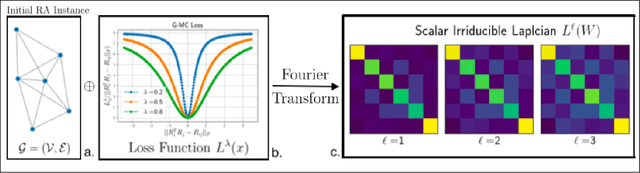
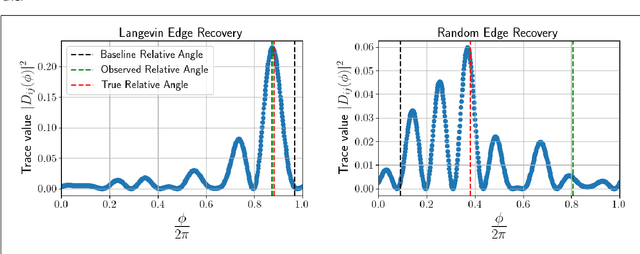
Abstract:Rotation averaging (RA) is a fundamental problem in robotics and computer vision. In RA, the goal is to estimate a set of $N$ unknown orientations $R_{1}, ..., R_{N} \in SO(3)$, given noisy measurements $R_{ij} \sim R^{-1}_{i} R_{j}$ of a subset of their pairwise relative rotations. This problem is both nonconvex and NP-hard, and thus difficult to solve in the general case. We apply harmonic analysis on compact groups to derive a (convex) spectral relaxation constructed from truncated Fourier decompositions of the individual summands appearing in the RA objective; we then recover an estimate of the RA solution by computing a few extremal eigenpairs of this relaxation, and (approximately) solving a consensus problem. Our approach affords several notable advantages versus prior RA methods: it can be used in conjunction with \emph{any} smooth loss function (including, but not limited to, robust M-estimators), does not require any initialization, and is implemented using only simple (and highly scalable) linear-algebraic computations and parallelizable optimizations over band-limited functions of individual rotational states. Moreover, under the (physically well-motivated) assumption of multiplicative Langevin measurement noise, we derive explicit performance guarantees for our spectral estimator (in the form of probabilistic tail bounds on the estimation error) that are parameterized in terms of graph-theoretic quantities of the underlying measurement network. By concretely linking estimator performance with properties of the underlying measurement graph, our results also indicate how to devise measurement networks that are \emph{guaranteed} to achieve accurate estimation, enabling such downstream tasks as sensor placement, network compression, and active sensing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge