Alan Papalia
Sparse Variable Projection in Robotic Perception: Exploiting Separable Structure for Efficient Nonlinear Optimization
Dec 08, 2025Abstract:Robotic perception often requires solving large nonlinear least-squares (NLS) problems. While sparsity has been well-exploited to scale solvers, a complementary and underexploited structure is \emph{separability} -- where some variables (e.g., visual landmarks) appear linearly in the residuals and, for any estimate of the remaining variables (e.g., poses), have a closed-form solution. Variable projection (VarPro) methods are a family of techniques that exploit this structure by analytically eliminating the linear variables and presenting a reduced problem in the remaining variables that has favorable properties. However, VarPro has seen limited use in robotic perception; a major challenge arises from gauge symmetries (e.g., cost invariance to global shifts and rotations), which are common in perception and induce specific computational challenges in standard VarPro approaches. We present a VarPro scheme designed for problems with gauge symmetries that jointly exploits separability and sparsity. Our method can be applied as a one-time preprocessing step to construct a \emph{matrix-free Schur complement operator}. This operator allows efficient evaluation of costs, gradients, and Hessian-vector products of the reduced problem and readily integrates with standard iterative NLS solvers. We provide precise conditions under which our method applies, and describe extensions when these conditions are only partially met. Across synthetic and real benchmarks in SLAM, SNL, and SfM, our approach achieves up to \textbf{2$\times$--35$\times$ faster runtimes} than state-of-the-art methods while maintaining accuracy. We release an open-source C++ implementation and all datasets from our experiments.
Practical and Performant Enhancements for Maximization of Algebraic Connectivity
Nov 11, 2025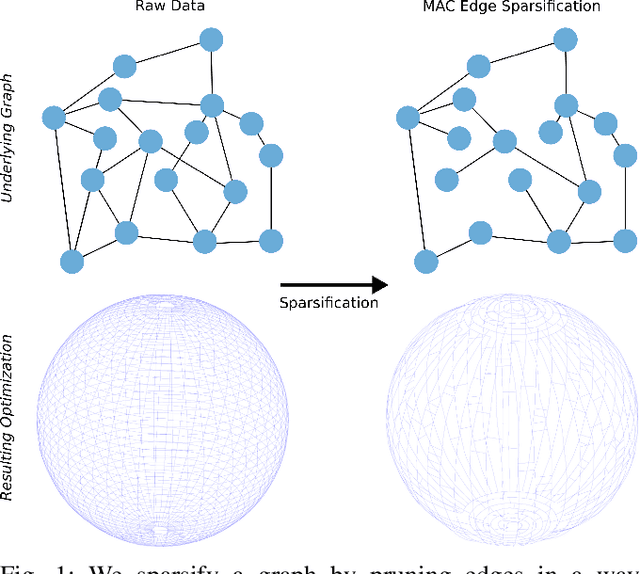
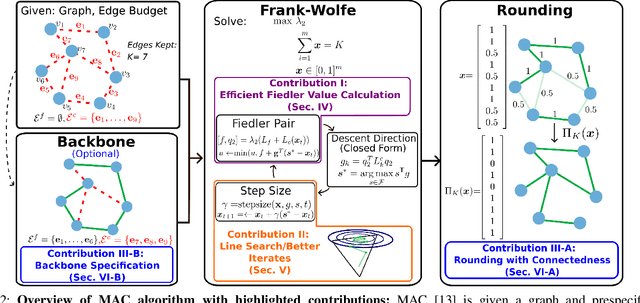
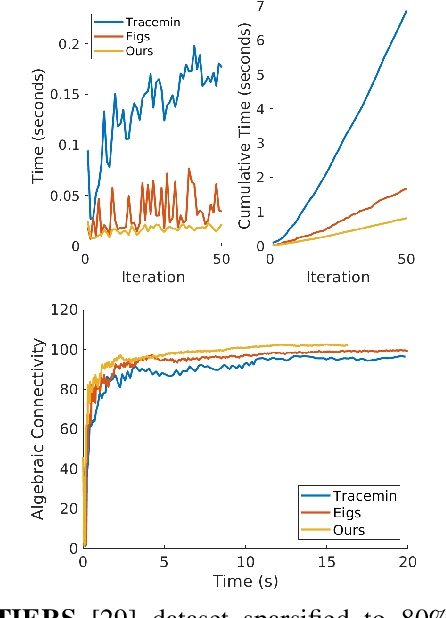
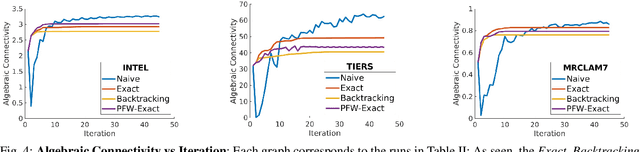
Abstract:Long-term state estimation over graphs remains challenging as current graph estimation methods scale poorly on large, long-term graphs. To address this, our work advances a current state-of-the-art graph sparsification algorithm, maximizing algebraic connectivity (MAC). MAC is a sparsification method that preserves estimation performance by maximizing the algebraic connectivity, a spectral graph property that is directly connected to the estimation error. Unfortunately, MAC remains computationally prohibitive for online use and requires users to manually pre-specify a connectivity-preserving edge set. Our contributions close these gaps along three complementary fronts: we develop a specialized solver for algebraic connectivity that yields an average 2x runtime speedup; we investigate advanced step size strategies for MAC's optimization procedure to enhance both convergence speed and solution quality; and we propose automatic schemes that guarantee graph connectivity without requiring manual specification of edges. Together, these contributions make MAC more scalable, reliable, and suitable for real-time estimation applications.
A Roadmap for Climate-Relevant Robotics Research
Jul 15, 2025



Abstract:Climate change is one of the defining challenges of the 21st century, and many in the robotics community are looking for ways to contribute. This paper presents a roadmap for climate-relevant robotics research, identifying high-impact opportunities for collaboration between roboticists and experts across climate domains such as energy, the built environment, transportation, industry, land use, and Earth sciences. These applications include problems such as energy systems optimization, construction, precision agriculture, building envelope retrofits, autonomous trucking, and large-scale environmental monitoring. Critically, we include opportunities to apply not only physical robots but also the broader robotics toolkit - including planning, perception, control, and estimation algorithms - to climate-relevant problems. A central goal of this roadmap is to inspire new research directions and collaboration by highlighting specific, actionable problems at the intersection of robotics and climate. This work represents a collaboration between robotics researchers and domain experts in various climate disciplines, and it serves as an invitation to the robotics community to bring their expertise to bear on urgent climate priorities.
Learning Smooth State-Dependent Traversability from Dense Point Clouds
Jun 04, 2025Abstract:A key open challenge in off-road autonomy is that the traversability of terrain often depends on the vehicle's state. In particular, some obstacles are only traversable from some orientations. However, learning this interaction by encoding the angle of approach as a model input demands a large and diverse training dataset and is computationally inefficient during planning due to repeated model inference. To address these challenges, we present SPARTA, a method for estimating approach angle conditioned traversability from point clouds. Specifically, we impose geometric structure into our network by outputting a smooth analytical function over the 1-Sphere that predicts risk distribution for any angle of approach with minimal overhead and can be reused for subsequent queries. The function is composed of Fourier basis functions, which has important advantages for generalization due to their periodic nature and smoothness. We demonstrate SPARTA both in a high-fidelity simulation platform, where our model achieves a 91\% success rate crossing a 40m boulder field (compared to 73\% for the baseline), and on hardware, illustrating the generalization ability of the model to real-world settings.
Distributed Certifiably Correct Range-Aided SLAM
Mar 05, 2025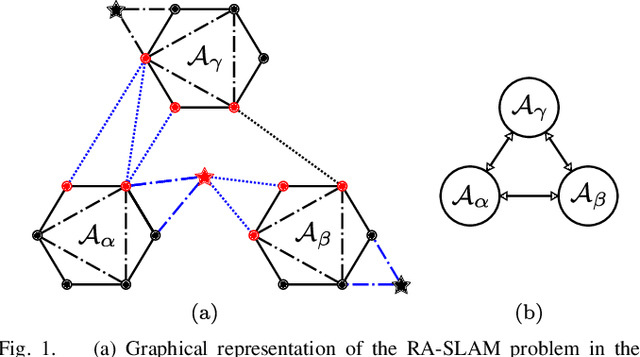
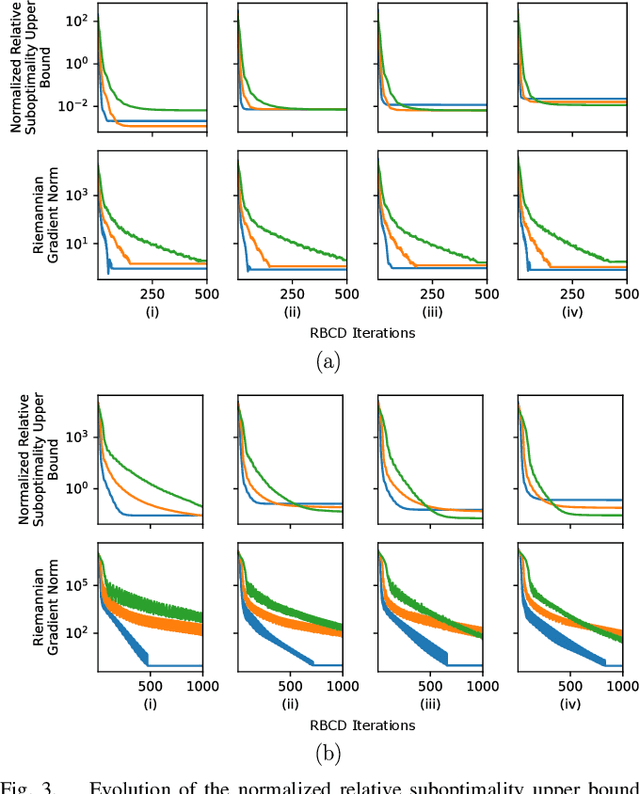
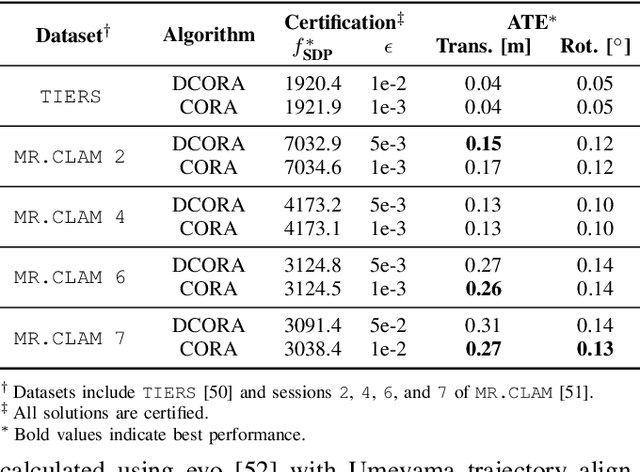
Abstract:Reliable simultaneous localization and mapping (SLAM) algorithms are necessary for safety-critical autonomous navigation. In the communication-constrained multi-agent setting, navigation systems increasingly use point-to-point range sensors as they afford measurements with low bandwidth requirements and known data association. The state estimation problem for these systems takes the form of range-aided (RA) SLAM. However, distributed algorithms for solving the RA-SLAM problem lack formal guarantees on the quality of the returned estimate. To this end, we present the first distributed algorithm for RA-SLAM that can efficiently recover certifiably globally optimal solutions. Our algorithm, distributed certifiably correct RA-SLAM (DCORA), achieves this via the Riemannian Staircase method, where computational procedures developed for distributed certifiably correct pose graph optimization are generalized to the RA-SLAM problem. We demonstrate DCORA's efficacy on real-world multi-agent datasets by achieving absolute trajectory errors comparable to those of a state-of-the-art centralized certifiably correct RA-SLAM algorithm. Additionally, we perform a parametric study on the structure of the RA-SLAM problem using synthetic data, revealing how common parameters affect DCORA's performance.
MAC: Maximizing Algebraic Connectivity for Graph Sparsification
Mar 28, 2024



Abstract:Simultaneous localization and mapping (SLAM) is a critical capability in autonomous navigation, but memory and computational limits make long-term application of common SLAM techniques impractical; a robot must be able to determine what information should be retained and what can safely be forgotten. In graph-based SLAM, the number of edges (measurements) in a pose graph determines both the memory requirements of storing a robot's observations and the computational expense of algorithms deployed for performing state estimation using those observations, both of which can grow unbounded during long-term navigation. Motivated by these challenges, we propose a new general purpose approach to sparsify graphs in a manner that maximizes algebraic connectivity, a key spectral property of graphs which has been shown to control the estimation error of pose graph SLAM solutions. Our algorithm, MAC (for maximizing algebraic connectivity), is simple and computationally inexpensive, and admits formal post hoc performance guarantees on the quality of the solution that it provides. In application to the problem of pose-graph SLAM, we show on several benchmark datasets that our approach quickly produces high-quality sparsification results which retain the connectivity of the graph and, in turn, the quality of corresponding SLAM solutions.
Certifiably Correct Range-Aided SLAM
Feb 22, 2023Abstract:We present the first algorithm capable of efficiently computing certifiably optimal solutions to range-aided simultaneous localization and mapping (RA-SLAM) problems. Robotic navigation systems are increasingly incorporating point-to-point ranging sensors, leading state estimation which takes the form of RA-SLAM. However, the RA-SLAM problem is more difficult to solve than traditional pose-graph SLAM; ranging sensor models introduce additional non-convexity, unlike pose-pose or pose-landmark measurements, a single range measurement does not uniquely determine the relative transform between the involved sensors, and RA-SLAM inference is highly sensitive to initial estimates. Our approach relaxes the RA-SLAM problem to a semidefinite program (SDP), which we show how to solve efficiently using the Riemannian staircase methodology. The solution of this SDP provides a high-quality initialization for our original RA-SLAM problem, which is subsequently refined via local optimization, as well as a lower-bound on the RA-SLAM problem's optimal value. Our algorithm, named certifiably correct RA-SLAM (CORA), applies to problems comprised of arbitrary pose-pose, pose-landmark, and ranging measurements. Evaluation on simulated and real-world marine examples shows that our algorithm frequently produces certifiably optimal RA-SLAM solutions; moreover, even suboptimal estimates are typically within 1-2\% of the optimal value.
SCORE: A Second-Order Conic Initialization for Range-Aided SLAM
Oct 06, 2022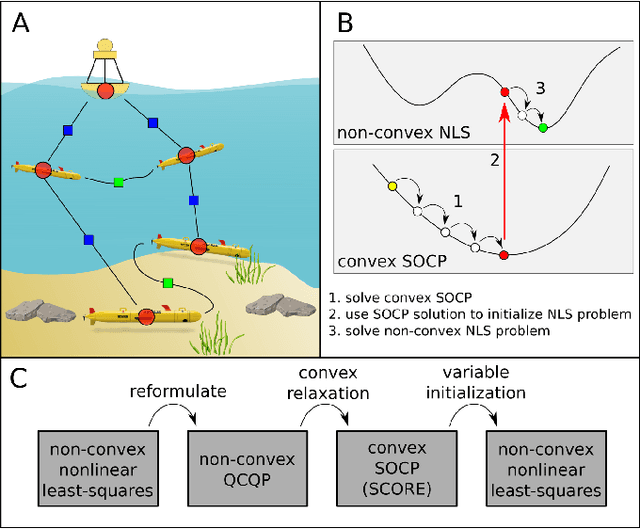
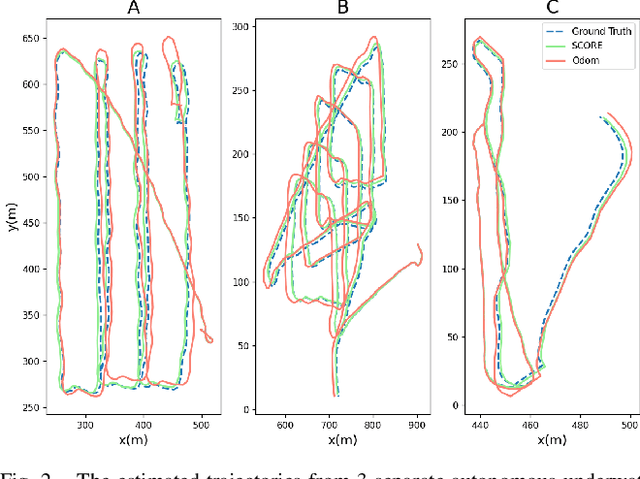
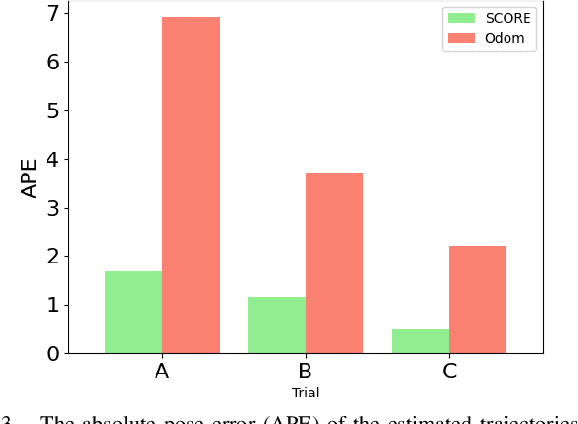
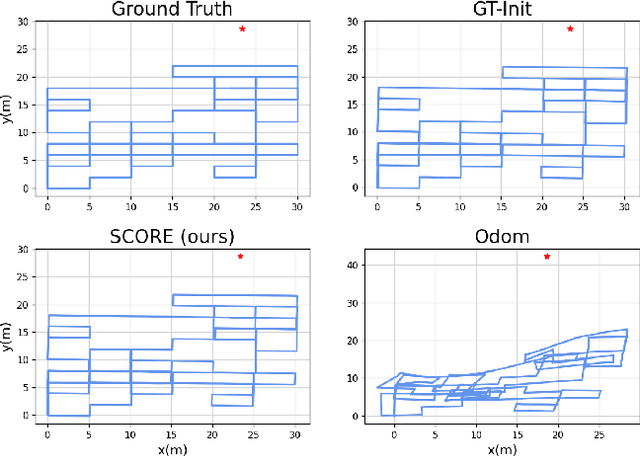
Abstract:We present a novel initialization technique for the range-aided simultaneous localization and mapping (RA-SLAM) problem. In RA-SLAM we consider measurements of point-to-point distances in addition to measurements of rigid transformations to landmark or pose variables. Standard formulations of RA-SLAM approach the problem as non-convex optimization, which requires a good initialization to obtain quality results. The initialization technique proposed here relaxes the RA-SLAM problem to a convex problem which is then solved to determine an initialization for the original, non-convex problem. The relaxation is a second-order cone program (SOCP), which is derived from a quadratically constrained quadratic program (QCQP) formulation of the RA-SLAM problem. As a SOCP, the method is highly scalable. We name this relaxation Second-order COnic RElaxation for RA-SLAM (SCORE). To our knowledge, this work represents the first convex relaxation for RA-SLAM. We present real-world and simulated experiments which show SCORE initialization permits the efficient recovery of quality solutions for a variety of challenging single- and multi-robot RA-SLAM problems with thousands of poses and range measurements.
On Reference Solutions to Non-Gaussian SLAM Factor Graphs
Sep 22, 2021
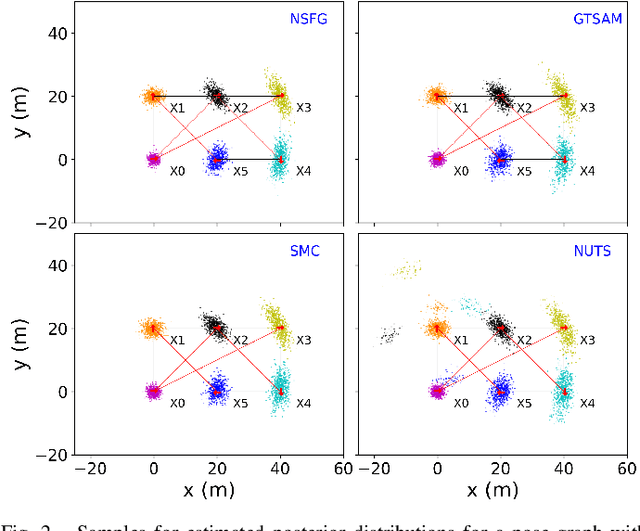
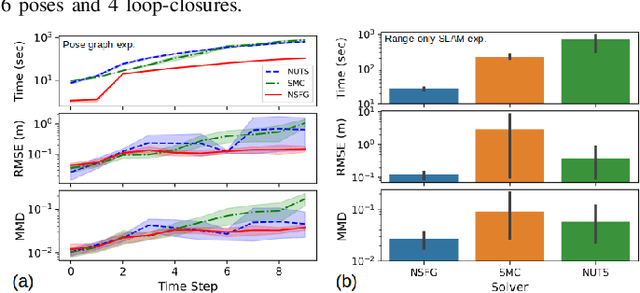

Abstract:Many real-world applications of simultaneous localization and mapping (SLAM) require approximate inference approaches, as exact inference for high-dimensional non-Gaussian posterior distributions is often computationally intractable. There are substantial challenges, however, in evaluating the quality of a solution provided by such inference techniques. One approach to solution evaluation is to solve the non-Gaussian posteriors with a more computationally expensive but generally accurate approach to create a reference solution for side-by-side comparison. Our work takes this direction. This paper presents nested sampling for factor graphs (NSFG), a nested-sampling-based approach for posterior estimation in non-Gaussian factor graph inference. Although NSFG applies to any problem modeled as inference over a factor graph, we focus on providing reference solutions for evaluation of approximate inference approaches to SLAM problems. The sparsity structure of SLAM factor graphs is exploited for improved computational performance without sacrificing solution quality. We compare NSFG to two other sampling-based approaches, the No-U-Turn sampler (NUTS) and sequential Monte Carlo (SMC), as well as GTSAM, a state-of-the-art Gaussian SLAM solver. We evaluate across several synthetic examples of interest to the non-Gaussian SLAM community, including multi-robot range-only SLAM and range-only SLAM with ambiguous data associations. Quantitative and qualitative analyses show NSFG is capable of producing high-fidelity solutions to a wide range of non-Gaussian SLAM problems, with notably superior solutions than NUTS and SMC. In addition, NSFG demonstrated improved scalability over NUTS and SMC.
Prioritized Planning for Cooperative Range-Only Localization in Multi-Robot Networks
Sep 10, 2021
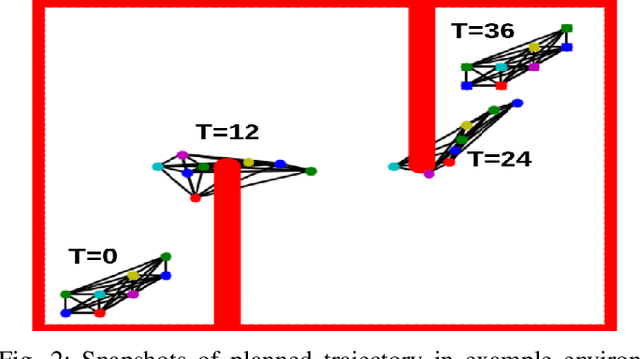
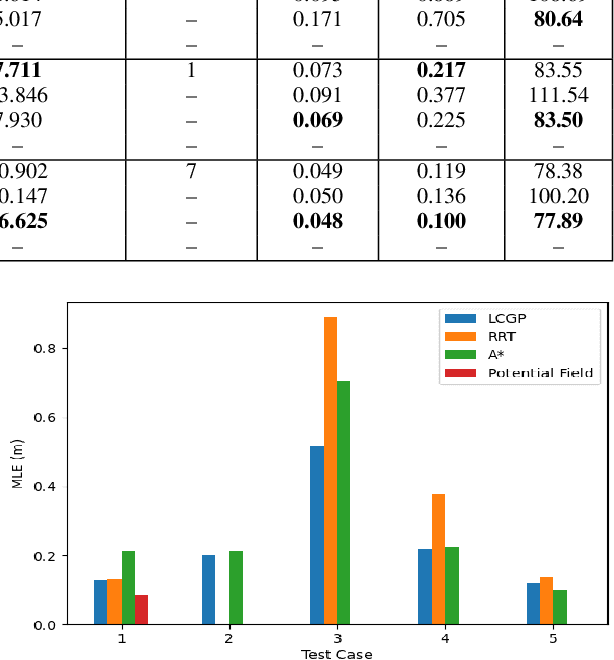
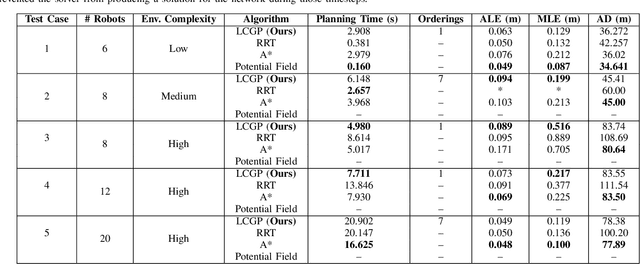
Abstract:We present a novel path-planning algorithm to reduce localization error for a network of robots cooperatively localizing via inter-robot range measurements. The quality of localization with range measurements depends on the configuration of the network, and poor configurations can cause substantial localization errors. To reduce the effect of network configuration on localization error for moving networks we consider various optimality measures of the Fisher information matrix (FIM), which have well-studied relationships with the localization error. In particular, we pose a trajectory planning problem with constraints on the FIM optimality measures. By constraining these optimality measures we can control the statistical properties of the localization error. To efficiently generate trajectories which satisfy these FIM constraints we present a prioritized planner which leverages graph-based planning and unique properties of the range-only FIM. We show results in simulated experiments that demonstrate the trajectories generated by our algorithm reduce worst-case localization error by up to 42\% in comparison to existing planning approaches and can scalably plan distance-efficient trajectories in complicated environments for large numbers of robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge