David M. Rosen
Distributed Certifiably Correct Range-Aided SLAM
Mar 05, 2025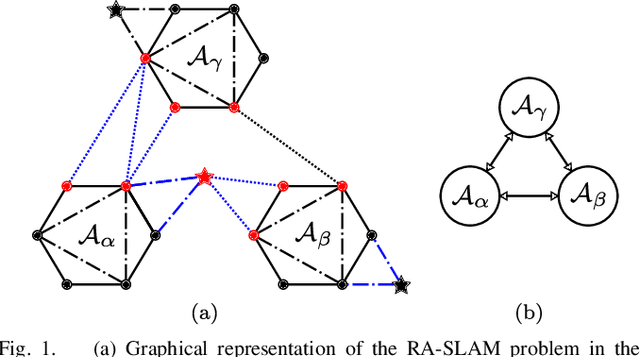
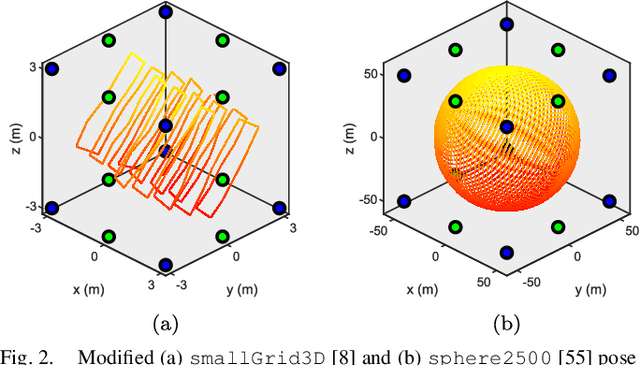
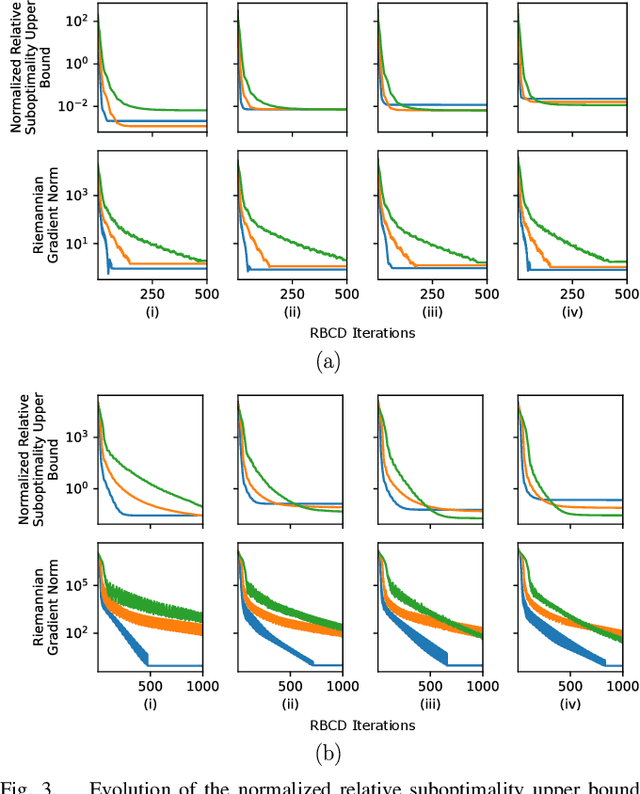
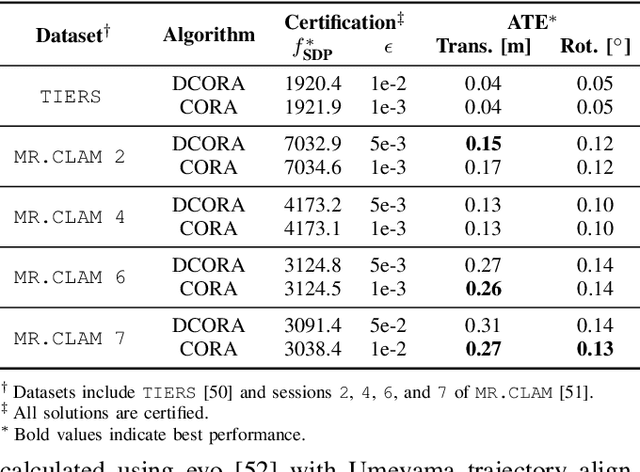
Abstract:Reliable simultaneous localization and mapping (SLAM) algorithms are necessary for safety-critical autonomous navigation. In the communication-constrained multi-agent setting, navigation systems increasingly use point-to-point range sensors as they afford measurements with low bandwidth requirements and known data association. The state estimation problem for these systems takes the form of range-aided (RA) SLAM. However, distributed algorithms for solving the RA-SLAM problem lack formal guarantees on the quality of the returned estimate. To this end, we present the first distributed algorithm for RA-SLAM that can efficiently recover certifiably globally optimal solutions. Our algorithm, distributed certifiably correct RA-SLAM (DCORA), achieves this via the Riemannian Staircase method, where computational procedures developed for distributed certifiably correct pose graph optimization are generalized to the RA-SLAM problem. We demonstrate DCORA's efficacy on real-world multi-agent datasets by achieving absolute trajectory errors comparable to those of a state-of-the-art centralized certifiably correct RA-SLAM algorithm. Additionally, we perform a parametric study on the structure of the RA-SLAM problem using synthetic data, revealing how common parameters affect DCORA's performance.
A Trust-Region Method for Graphical Stein Variational Inference
Oct 21, 2024Abstract:Stein variational inference (SVI) is a sample-based approximate Bayesian inference technique that generates a sample set by jointly optimizing the samples' locations to minimize an information-theoretic measure of discrepancy with the target probability distribution. SVI thus provides a fast and significantly more sample-efficient approach to Bayesian inference than traditional (random-sampling-based) alternatives. However, the optimization techniques employed in existing SVI methods struggle to address problems in which the target distribution is high-dimensional, poorly-conditioned, or non-convex, which severely limits the range of their practical applicability. In this paper, we propose a novel trust-region optimization approach for SVI that successfully addresses each of these challenges. Our method builds upon prior work in SVI by leveraging conditional independences in the target distribution (to achieve high-dimensional scaling) and second-order information (to address poor conditioning), while additionally providing an effective adaptive step control procedure, which is essential for ensuring convergence on challenging non-convex optimization problems. Experimental results show our method achieves superior numerical performance, both in convergence rate and sample accuracy, and scales better in high-dimensional distributions, than previous SVI techniques.
OASIS: Optimal Arrangements for Sensing in SLAM
Sep 19, 2023Abstract:The number and arrangement of sensors on an autonomous mobile robot dramatically influence its perception capabilities. Ensuring that sensors are mounted in a manner that enables accurate detection, localization, and mapping is essential for the success of downstream control tasks. However, when designing a new robotic platform, researchers and practitioners alike usually mimic standard configurations or maximize simple heuristics like field-of-view (FOV) coverage to decide where to place exteroceptive sensors. In this work, we conduct an information-theoretic investigation of this overlooked element of mobile robotic perception in the context of simultaneous localization and mapping (SLAM). We show how to formalize the sensor arrangement problem as a form of subset selection under the E-optimality performance criterion. While this formulation is NP-hard in general, we further show that a combination of greedy sensor selection and fast convex relaxation-based post-hoc verification enables the efficient recovery of certifiably optimal sensor designs in practice. Results from synthetic experiments reveal that sensors placed with OASIS outperform benchmarks in terms of mean squared error of visual SLAM estimates.
Certifiably Correct Range-Aided SLAM
Feb 22, 2023Abstract:We present the first algorithm capable of efficiently computing certifiably optimal solutions to range-aided simultaneous localization and mapping (RA-SLAM) problems. Robotic navigation systems are increasingly incorporating point-to-point ranging sensors, leading state estimation which takes the form of RA-SLAM. However, the RA-SLAM problem is more difficult to solve than traditional pose-graph SLAM; ranging sensor models introduce additional non-convexity, unlike pose-pose or pose-landmark measurements, a single range measurement does not uniquely determine the relative transform between the involved sensors, and RA-SLAM inference is highly sensitive to initial estimates. Our approach relaxes the RA-SLAM problem to a semidefinite program (SDP), which we show how to solve efficiently using the Riemannian staircase methodology. The solution of this SDP provides a high-quality initialization for our original RA-SLAM problem, which is subsequently refined via local optimization, as well as a lower-bound on the RA-SLAM problem's optimal value. Our algorithm, named certifiably correct RA-SLAM (CORA), applies to problems comprised of arbitrary pose-pose, pose-landmark, and ranging measurements. Evaluation on simulated and real-world marine examples shows that our algorithm frequently produces certifiably optimal RA-SLAM solutions; moreover, even suboptimal estimates are typically within 1-2\% of the optimal value.
SCORE: A Second-Order Conic Initialization for Range-Aided SLAM
Oct 06, 2022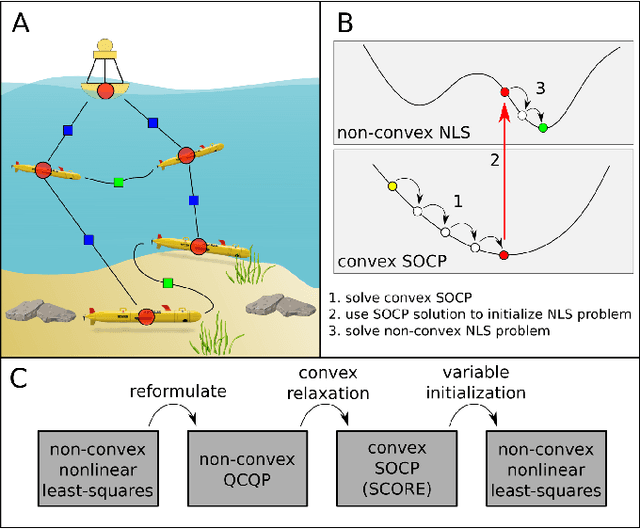
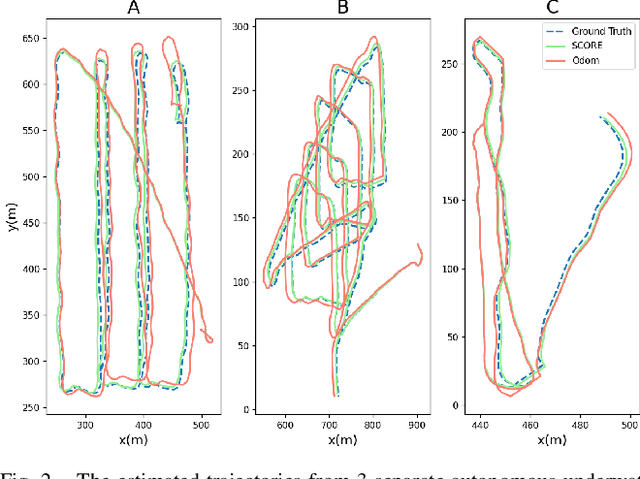
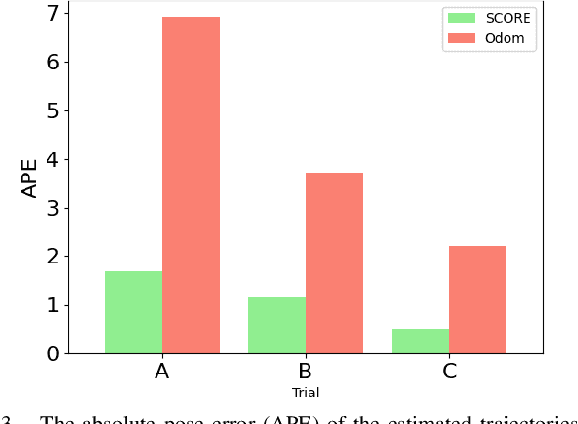
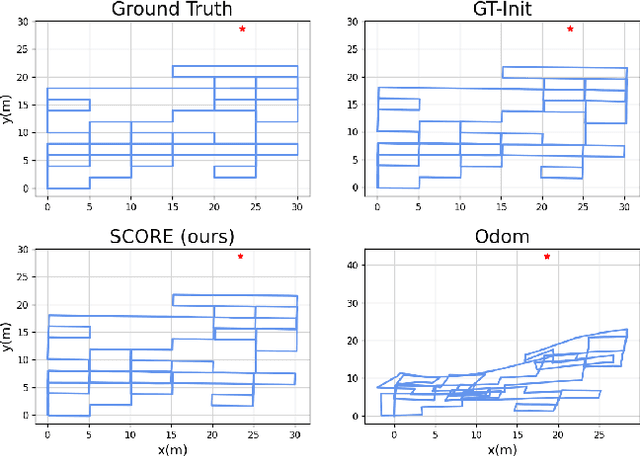
Abstract:We present a novel initialization technique for the range-aided simultaneous localization and mapping (RA-SLAM) problem. In RA-SLAM we consider measurements of point-to-point distances in addition to measurements of rigid transformations to landmark or pose variables. Standard formulations of RA-SLAM approach the problem as non-convex optimization, which requires a good initialization to obtain quality results. The initialization technique proposed here relaxes the RA-SLAM problem to a convex problem which is then solved to determine an initialization for the original, non-convex problem. The relaxation is a second-order cone program (SOCP), which is derived from a quadratically constrained quadratic program (QCQP) formulation of the RA-SLAM problem. As a SOCP, the method is highly scalable. We name this relaxation Second-order COnic RElaxation for RA-SLAM (SCORE). To our knowledge, this work represents the first convex relaxation for RA-SLAM. We present real-world and simulated experiments which show SCORE initialization permits the efficient recovery of quality solutions for a variety of challenging single- and multi-robot RA-SLAM problems with thousands of poses and range measurements.
Accelerating Certifiable Estimation with Preconditioned Eigensolvers
Jul 12, 2022

Abstract:Convex (specifically semidefinite) relaxation provides a powerful approach to constructing robust machine perception systems, enabling the recovery of certifiably globally optimal solutions of challenging estimation problems in many practical settings. However, solving the large-scale semidefinite relaxations underpinning this approach remains a formidable computational challenge. A dominant cost in many state-of-the-art (Burer-Monteiro factorization-based) certifiable estimation methods is solution verification (testing the global optimality of a given candidate solution), which entails computing a minimum eigenpair of a certain symmetric certificate matrix. In this paper, we show how to significantly accelerate this verification step, and thereby the overall speed of certifiable estimation methods. First, we show that the certificate matrices arising in the Burer-Monteiro approach generically possess spectra that make the verification problem expensive to solve using standard iterative eigenvalue methods. We then show how to address this challenge using preconditioned eigensolvers; specifically, we design a specialized solution verification algorithm based upon the locally optimal block preconditioned conjugate gradient (LOBPCG) method together with a simple yet highly effective algebraic preconditioner. Experimental evaluation on a variety of simulated and real-world examples shows that our proposed verification scheme is very effective in practice, accelerating solution verification by up to 280x, and the overall Burer-Monteiro method by up to 16x, versus the standard Lanczos method when applied to relaxations derived from large-scale SLAM benchmarks.
Spectral Measurement Sparsification for Pose-Graph SLAM
Mar 25, 2022


Abstract:Simultaneous localization and mapping (SLAM) is a critical capability in autonomous navigation, but in order to scale SLAM to the setting of "lifelong" SLAM, particularly under memory or computation constraints, a robot must be able to determine what information should be retained and what can safely be forgotten. In graph-based SLAM, the number of edges (measurements) in a pose graph determines both the memory requirements of storing a robot's observations and the computational expense of algorithms deployed for performing state estimation using those observations; both of which can grow unbounded during long-term navigation. To address this, we propose a spectral approach for pose graph sparsification which maximizes the algebraic connectivity of the sparsified measurement graphs, a key quantity which has been shown to control the estimation error of pose graph SLAM solutions. Our algorithm, MAC (for "maximizing algebraic connectivity"), which is based on convex relaxation, is simple and computationally inexpensive, and admits formal post hoc performance guarantees on the quality of the solutions it provides. In experiments on benchmark pose-graph SLAM datasets, we show that our approach quickly produces high-quality sparsification results which retain the connectivity of the graph and, in turn, the quality of corresponding SLAM solutions, as compared to a baseline approach which does not consider graph connectivity.
Distributed Riemannian Optimization with Lazy Communication for Collaborative Geometric Estimation
Mar 02, 2022


Abstract:We present the first distributed optimization algorithm with lazy communication for collaborative geometric estimation, the backbone of modern collaborative simultaneous localization and mapping (SLAM) and structure-from-motion (SfM) applications. Our method allows agents to cooperatively reconstruct a shared geometric model on a central server by fusing individual observations, but without the need to transmit potentially sensitive information about the agents themselves (such as their locations). Furthermore, to alleviate the burden of communication during iterative optimization, we design a set of communication triggering conditions that enable agents to selectively upload local information that are useful to global optimization. Our approach thus achieves significant communication reduction with minimal impact on optimization performance. As our main theoretical contribution, we prove that our method converges to first-order critical points with a sublinear convergence rate. Numerical evaluations on bundle adjustment problems from collaborative SLAM and SfM datasets show that our method performs competitively against existing distributed techniques, while achieving up to 78% total communication reduction.
Performance Guarantees for Spectral Initialization in Rotation Averaging and Pose-Graph SLAM
Jan 11, 2022



Abstract:In this work we present the first initialization methods equipped with explicit performance guarantees adapted to the pose-graph simultaneous localization and mapping (SLAM) and rotation averaging (RA) problems. SLAM and rotation averaging are typically formalized as large-scale nonconvex point estimation problems, with many bad local minima that can entrap the smooth optimization methods typically applied to solve them; the performance of standard SLAM and RA algorithms thus crucially depends upon the quality of the estimates used to initialize this local search. While many initialization methods for SLAM and RA have appeared in the literature, these are typically obtained as purely heuristic approximations, making it difficult to determine whether (or under what circumstances) these techniques can be reliably deployed. In contrast, in this work we study the problem of initialization through the lens of spectral relaxation. Specifically, we derive a simple spectral relaxation of SLAM and RA, the form of which enables us to exploit classical linear-algebraic techniques (eigenvector perturbation bounds) to control the distance from our spectral estimate to both the (unknown) ground-truth and the global minimizer of the estimation problem as a function of measurement noise. Our results reveal the critical role that spectral graph-theoretic properties of the measurement network play in controlling estimation accuracy; moreover, as a by-product of our analysis we obtain new bounds on the estimation error for the maximum likelihood estimators in SLAM and RA, which are likely to be of independent interest. Finally, we show experimentally that our spectral estimator is very effective in practice, producing initializations of comparable or superior quality at lower computational cost compared to existing state-of-the-art techniques.
Online Incremental Non-Gaussian Inference for SLAM Using Normalizing Flows
Oct 02, 2021
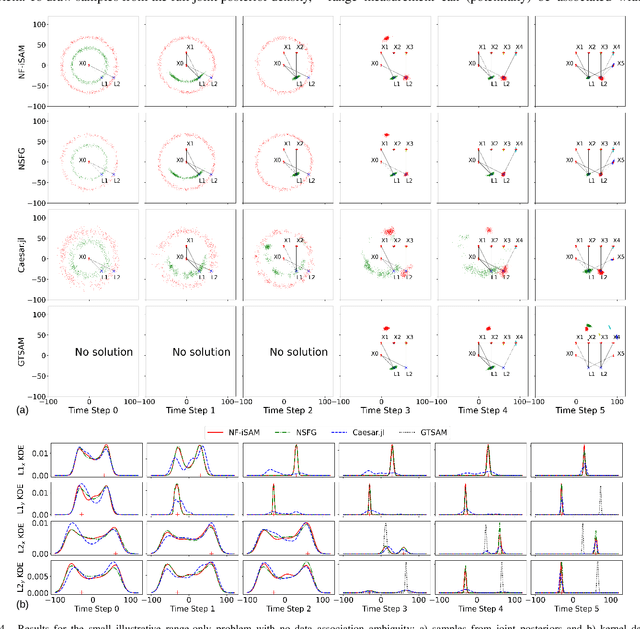
Abstract:This paper presents a novel non-Gaussian inference algorithm, Normalizing Flow iSAM (NF-iSAM), for solving SLAM problems with non-Gaussian factors and/or nonlinear measurement models. NF-iSAM exploits the expressive power of neural networks to model normalizing flows that can accurately approximate the joint posterior of highly nonlinear and non-Gaussian factor graphs. By leveraging the Bayes tree, NF-iSAM is able to exploit the sparsity structure of SLAM, thus enabling efficient incremental updates similar to iSAM2, although in the more challenging non-Gaussian setting. We demonstrate the performance of NF-iSAM and compare it against state-of-the-art algorithms such as iSAM2 (Gaussian) and mm-iSAM (non-Gaussian) in synthetic and real range-only SLAM datasets with data association ambiguity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge