SCORE: A Second-Order Conic Initialization for Range-Aided SLAM

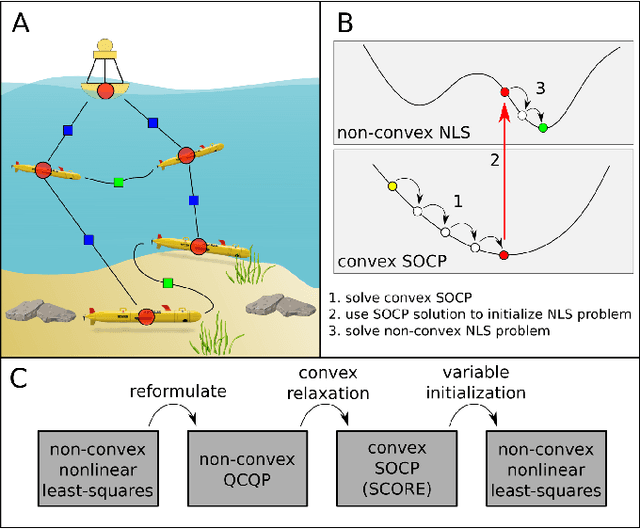
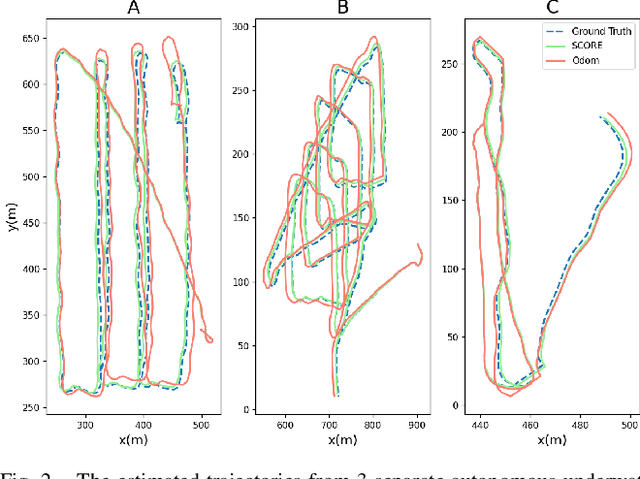
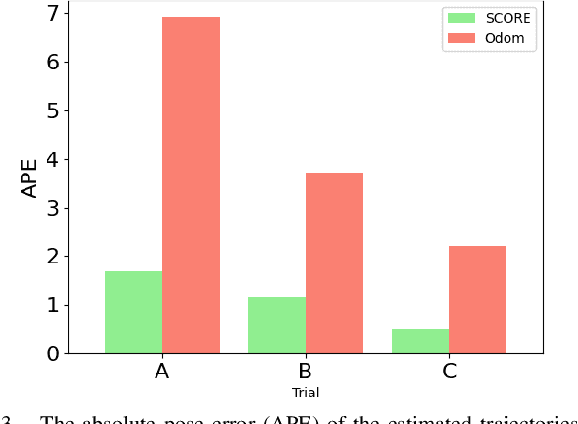
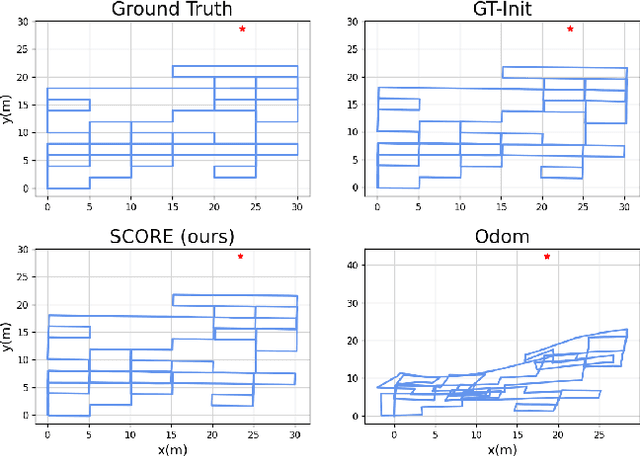
We present a novel initialization technique for the range-aided simultaneous localization and mapping (RA-SLAM) problem. In RA-SLAM we consider measurements of point-to-point distances in addition to measurements of rigid transformations to landmark or pose variables. Standard formulations of RA-SLAM approach the problem as non-convex optimization, which requires a good initialization to obtain quality results. The initialization technique proposed here relaxes the RA-SLAM problem to a convex problem which is then solved to determine an initialization for the original, non-convex problem. The relaxation is a second-order cone program (SOCP), which is derived from a quadratically constrained quadratic program (QCQP) formulation of the RA-SLAM problem. As a SOCP, the method is highly scalable. We name this relaxation Second-order COnic RElaxation for RA-SLAM (SCORE). To our knowledge, this work represents the first convex relaxation for RA-SLAM. We present real-world and simulated experiments which show SCORE initialization permits the efficient recovery of quality solutions for a variety of challenging single- and multi-robot RA-SLAM problems with thousands of poses and range measurements.

Discrete-Continuous Smoothing and Mapping

We describe a general approach to smoothing and mapping with a class of discrete-continuous factor graphs commonly encountered in robotics applications. While there are openly available tools providing flexible and easy-to-use interfaces for specifying and solving optimization problems formulated in terms of either discrete or continuous graphical models, at present, no similarly general tools exist enabling the same functionality for hybrid discrete-continuous problems. We aim to address this problem. In particular, we provide a library, DC-SAM, extending existing tools for optimization problems defined in terms of factor graphs to the setting of discrete-continuous models. A key contribution of our work is a novel solver for efficiently recovering approximate solutions to discrete-continuous optimization problems. The key insight to our approach is that while joint inference over continuous and discrete state spaces is often hard, many commonly encountered discrete-continuous problems can naturally be split into a "discrete part" and a "continuous part" that can individually be solved easily. Leveraging this structure, we optimize discrete and continuous variables in an alternating fashion. In consequence, our proposed work enables straightforward representation of and approximate inference in discrete-continuous graphical models. We also provide a method to recover the uncertainty in estimates of both discrete and continuous variables. We demonstrate the versatility of our approach through its application to three distinct robot perception applications: point-cloud registration, robust pose graph optimization, and object-based mapping and localization.

Spectral Measurement Sparsification for Pose-Graph SLAM

Simultaneous localization and mapping (SLAM) is a critical capability in autonomous navigation, but in order to scale SLAM to the setting of "lifelong" SLAM, particularly under memory or computation constraints, a robot must be able to determine what information should be retained and what can safely be forgotten. In graph-based SLAM, the number of edges (measurements) in a pose graph determines both the memory requirements of storing a robot's observations and the computational expense of algorithms deployed for performing state estimation using those observations; both of which can grow unbounded during long-term navigation. To address this, we propose a spectral approach for pose graph sparsification which maximizes the algebraic connectivity of the sparsified measurement graphs, a key quantity which has been shown to control the estimation error of pose graph SLAM solutions. Our algorithm, MAC (for "maximizing algebraic connectivity"), which is based on convex relaxation, is simple and computationally inexpensive, and admits formal post hoc performance guarantees on the quality of the solutions it provides. In experiments on benchmark pose-graph SLAM datasets, we show that our approach quickly produces high-quality sparsification results which retain the connectivity of the graph and, in turn, the quality of corresponding SLAM solutions, as compared to a baseline approach which does not consider graph connectivity.

Performance Guarantees for Spectral Initialization in Rotation Averaging and Pose-Graph SLAM

In this work we present the first initialization methods equipped with explicit performance guarantees adapted to the pose-graph simultaneous localization and mapping (SLAM) and rotation averaging (RA) problems. SLAM and rotation averaging are typically formalized as large-scale nonconvex point estimation problems, with many bad local minima that can entrap the smooth optimization methods typically applied to solve them; the performance of standard SLAM and RA algorithms thus crucially depends upon the quality of the estimates used to initialize this local search. While many initialization methods for SLAM and RA have appeared in the literature, these are typically obtained as purely heuristic approximations, making it difficult to determine whether (or under what circumstances) these techniques can be reliably deployed. In contrast, in this work we study the problem of initialization through the lens of spectral relaxation. Specifically, we derive a simple spectral relaxation of SLAM and RA, the form of which enables us to exploit classical linear-algebraic techniques (eigenvector perturbation bounds) to control the distance from our spectral estimate to both the (unknown) ground-truth and the global minimizer of the estimation problem as a function of measurement noise. Our results reveal the critical role that spectral graph-theoretic properties of the measurement network play in controlling estimation accuracy; moreover, as a by-product of our analysis we obtain new bounds on the estimation error for the maximum likelihood estimators in SLAM and RA, which are likely to be of independent interest. Finally, we show experimentally that our spectral estimator is very effective in practice, producing initializations of comparable or superior quality at lower computational cost compared to existing state-of-the-art techniques.

Advances in Inference and Representation for Simultaneous Localization and Mapping

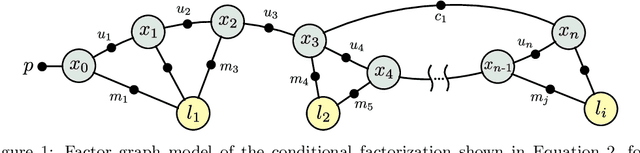
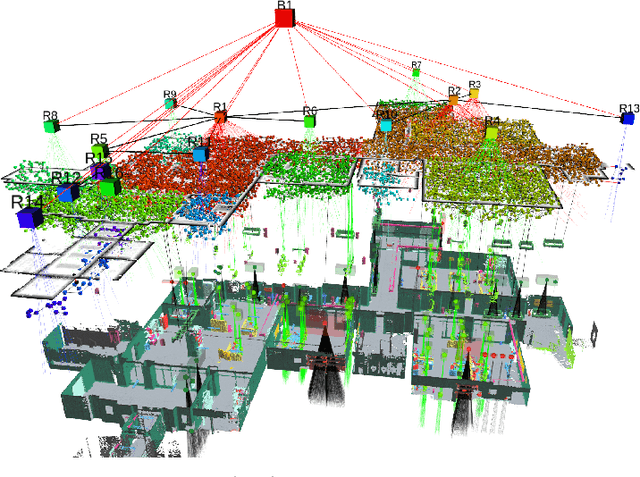
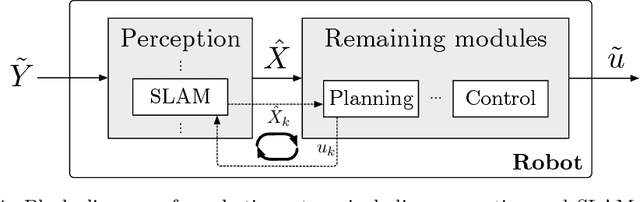
Simultaneous localization and mapping (SLAM) is the process of constructing a global model of an environment from local observations of it; this is a foundational capability for mobile robots, supporting such core functions as planning, navigation, and control. This article reviews recent progress in SLAM, focusing on advances in the expressive capacity of the environmental models used in SLAM systems (representation) and the performance of the algorithms used to estimate these models from data (inference). A prominent theme of recent SLAM research is the pursuit of environmental representations (including learned representations) that go beyond the classical attributes of geometry and appearance to model properties such as hierarchical organization, affordance, dynamics, and semantics; these advances equip autonomous agents with a more comprehensive understanding of the world, enabling more versatile and intelligent operation. A second major theme is a revitalized interest in the mathematical properties of the SLAM estimation problem itself (including its computational and information-theoretic performance limits); this work has led to the development of novel classes of certifiable and robust inference methods that dramatically improve the reliability of SLAM systems in real-world operation. We survey these advances with an emphasis on their ramifications for achieving robust, long-duration autonomy, and conclude with a discussion of open challenges and a perspective on future research directions.