On Reference Solutions to Non-Gaussian SLAM Factor Graphs

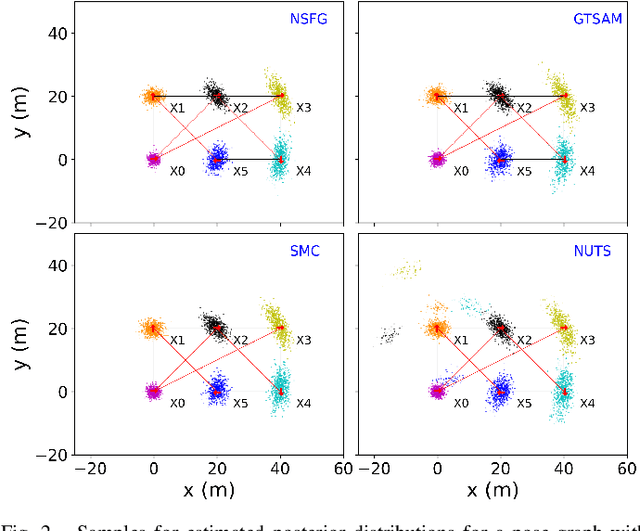
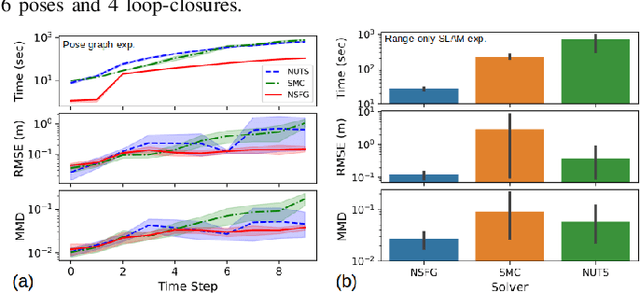
Many real-world applications of simultaneous localization and mapping (SLAM) require approximate inference approaches, as exact inference for high-dimensional non-Gaussian posterior distributions is often computationally intractable. There are substantial challenges, however, in evaluating the quality of a solution provided by such inference techniques. One approach to solution evaluation is to solve the non-Gaussian posteriors with a more computationally expensive but generally accurate approach to create a reference solution for side-by-side comparison. Our work takes this direction. This paper presents nested sampling for factor graphs (NSFG), a nested-sampling-based approach for posterior estimation in non-Gaussian factor graph inference. Although NSFG applies to any problem modeled as inference over a factor graph, we focus on providing reference solutions for evaluation of approximate inference approaches to SLAM problems. The sparsity structure of SLAM factor graphs is exploited for improved computational performance without sacrificing solution quality. We compare NSFG to two other sampling-based approaches, the No-U-Turn sampler (NUTS) and sequential Monte Carlo (SMC), as well as GTSAM, a state-of-the-art Gaussian SLAM solver. We evaluate across several synthetic examples of interest to the non-Gaussian SLAM community, including multi-robot range-only SLAM and range-only SLAM with ambiguous data associations. Quantitative and qualitative analyses show NSFG is capable of producing high-fidelity solutions to a wide range of non-Gaussian SLAM problems, with notably superior solutions than NUTS and SMC. In addition, NSFG demonstrated improved scalability over NUTS and SMC.