Point2Pose: Occlusion-Recovering 6D Pose Tracking and 3D Reconstruction for Multiple Unknown Objects Via 2D Point Trackers

We present Point2Pose, a model-free method for causal 6D pose tracking of multiple rigid objects from monocular RGB-D video. Initialized only from sparse image points on the objects to be tracked, our approach tracks multiple unseen objects without requiring object CAD models or category priors. Point2Pose leverages a 2D point tracker to obtain long-range correspondences, enabling instant recovery after complete occlusion. Simultaneously, the system incrementally reconstructs an online Truncated Signed Distance Function (TSDF) representation of the tracked targets. Alongside the method, we introduce a new multi-object tracking dataset comprising both simulation and real-world sequences, with motion-capture ground truth for evaluation. Experiments show that Point2Pose achieves performance comparable to the state-of-the-art methods on a severe-occlusion benchmark, while additionally supporting multi-object tracking and recovery from complete occlusion, capabilities that are not supported by previous model-free tracking approaches.

Practical and Performant Enhancements for Maximization of Algebraic Connectivity

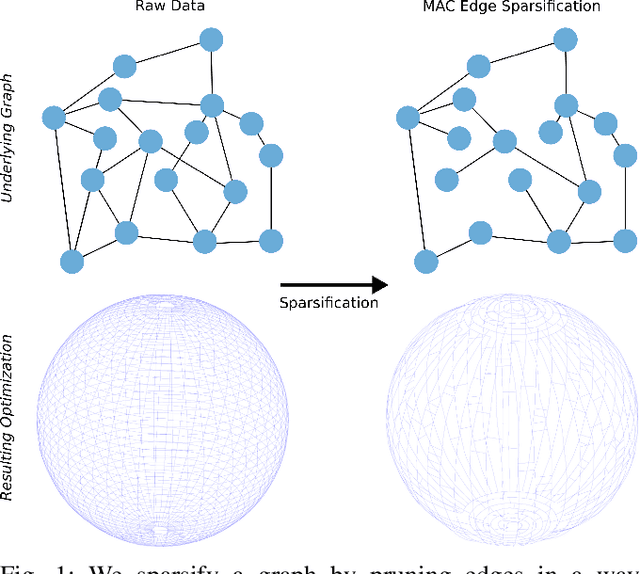
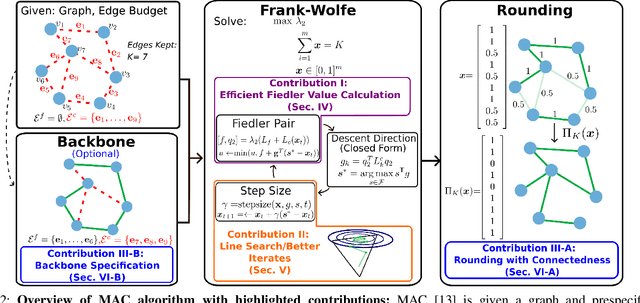
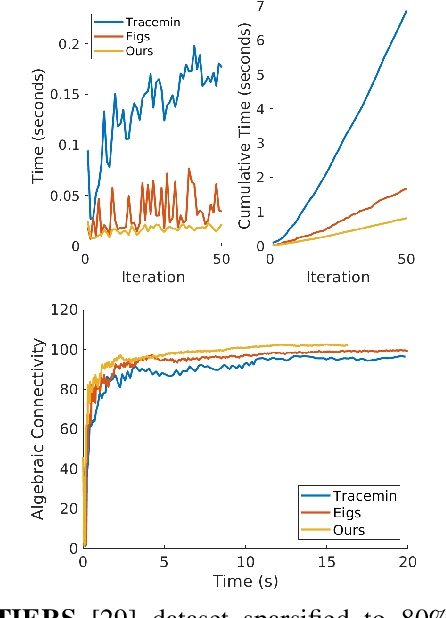
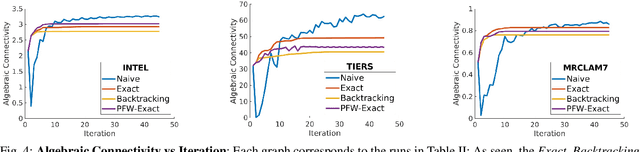
Long-term state estimation over graphs remains challenging as current graph estimation methods scale poorly on large, long-term graphs. To address this, our work advances a current state-of-the-art graph sparsification algorithm, maximizing algebraic connectivity (MAC). MAC is a sparsification method that preserves estimation performance by maximizing the algebraic connectivity, a spectral graph property that is directly connected to the estimation error. Unfortunately, MAC remains computationally prohibitive for online use and requires users to manually pre-specify a connectivity-preserving edge set. Our contributions close these gaps along three complementary fronts: we develop a specialized solver for algebraic connectivity that yields an average 2x runtime speedup; we investigate advanced step size strategies for MAC's optimization procedure to enhance both convergence speed and solution quality; and we propose automatic schemes that guarantee graph connectivity without requiring manual specification of edges. Together, these contributions make MAC more scalable, reliable, and suitable for real-time estimation applications.

MAC: Maximizing Algebraic Connectivity for Graph Sparsification

Simultaneous localization and mapping (SLAM) is a critical capability in autonomous navigation, but memory and computational limits make long-term application of common SLAM techniques impractical; a robot must be able to determine what information should be retained and what can safely be forgotten. In graph-based SLAM, the number of edges (measurements) in a pose graph determines both the memory requirements of storing a robot's observations and the computational expense of algorithms deployed for performing state estimation using those observations, both of which can grow unbounded during long-term navigation. Motivated by these challenges, we propose a new general purpose approach to sparsify graphs in a manner that maximizes algebraic connectivity, a key spectral property of graphs which has been shown to control the estimation error of pose graph SLAM solutions. Our algorithm, MAC (for maximizing algebraic connectivity), is simple and computationally inexpensive, and admits formal post hoc performance guarantees on the quality of the solution that it provides. In application to the problem of pose-graph SLAM, we show on several benchmark datasets that our approach quickly produces high-quality sparsification results which retain the connectivity of the graph and, in turn, the quality of corresponding SLAM solutions.

QCNN: Quadrature Convolutional Neural Network with Application to Unstructured Data Compression

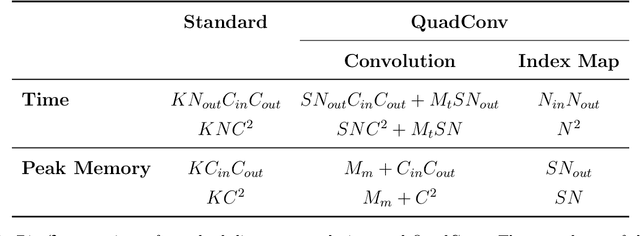
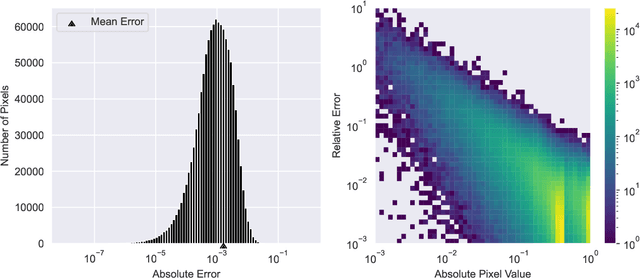
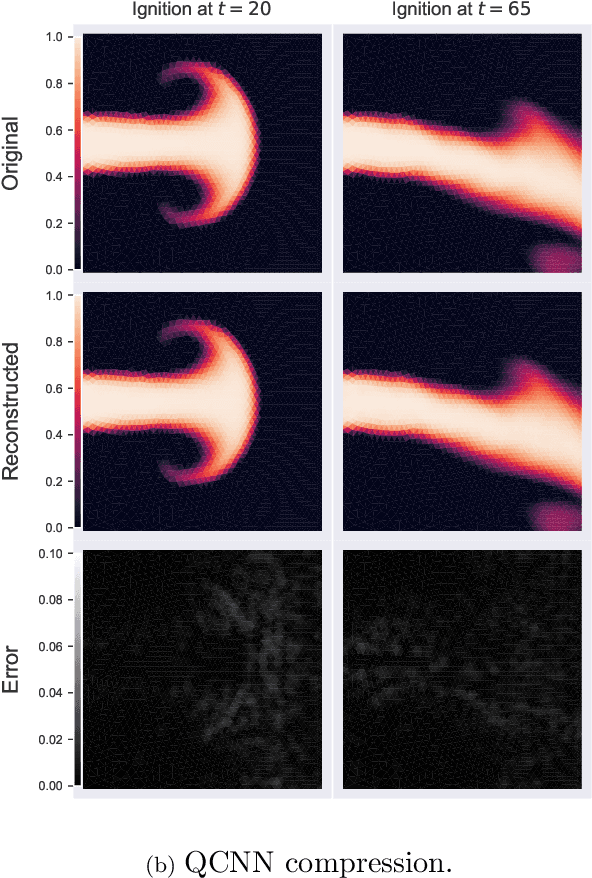
We present a new convolution layer for deep learning architectures which we call QuadConv -- an approximation to continuous convolution via quadrature. Our operator is developed explicitly for use on unstructured data, and accomplishes this by learning a continuous kernel that can be sampled at arbitrary locations. In the setting of neural compression, we show that a QuadConv-based autoencoder, resulting in a Quadrature Convolutional Neural Network (QCNN), can match the performance of standard discrete convolutions on structured uniform data, as in CNNs, and maintain this accuracy on unstructured data.

SLAM-Supported Self-Training for 6D Object Pose Estimation

Recent progress in learning-based object pose estimation paves the way for developing richer object-level world representations. However, the estimators, often trained with out-of-domain data, can suffer performance degradation as deployed in novel environments. To address the problem, we present a SLAM-supported self-training procedure to autonomously improve robot object pose estimation ability during navigation. Combining the network predictions with robot odometry, we can build a consistent object-level environment map via pose graph optimization (PGO). Exploiting the state estimates from PGO, we pseudo-label robot-collected RGB images to fine-tune the pose estimators. Unfortunately, it is difficult to quantify the uncertainty of the estimator predictions. The unmodeled data uncertainty used for PGO can result in low-quality object pose estimates. An automatic covariance tuning method is developed for robust PGO by allowing the measurement uncertainty models to change as part of the optimization process. The formulation permits a straightforward alternating minimization procedure that re-scales covariances analytically and component-wise, enabling more flexible noise modeling for learning-based measurements. We test our method with the deep object pose estimator (DOPE) on the YCB video dataset and in real-world robot experiments. The method can achieve significant performance gain in pose estimation, and in return facilitates the success of object SLAM.

A Multi-Hypothesis Approach to Pose Ambiguity in Object-Based SLAM

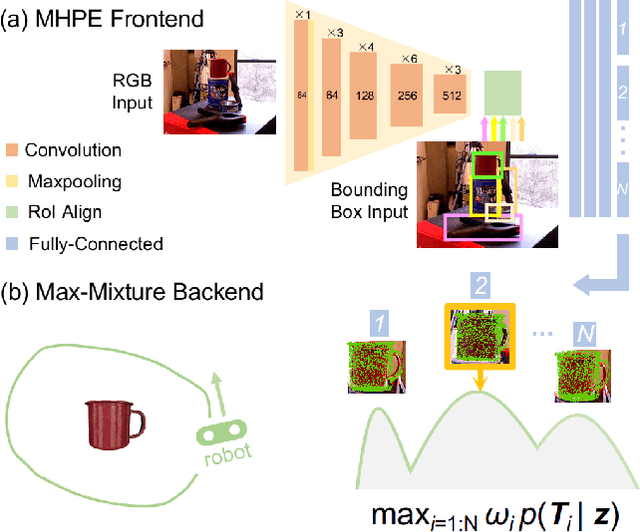
In object-based Simultaneous Localization and Mapping (SLAM), 6D object poses offer a compact representation of landmark geometry useful for downstream planning and manipulation tasks. However, measurement ambiguity then arises as objects may possess complete or partial object shape symmetries (e.g., due to occlusion), making it difficult or impossible to generate a single consistent object pose estimate. One idea is to generate multiple pose candidates to counteract measurement ambiguity. In this paper, we develop a novel approach that enables an object-based SLAM system to reason about multiple pose hypotheses for an object, and synthesize this locally ambiguous information into a globally consistent robot and landmark pose estimation formulation. In particular, we (1) present a learned pose estimation network that provides multiple hypotheses about the 6D pose of an object; (2) by treating the output of our network as components of a mixture model, we incorporate pose predictions into a SLAM system, which, over successive observations, recovers a globally consistent set of robot and object (landmark) pose estimates. We evaluate our approach on the popular YCB-Video Dataset and a simulated video featuring YCB objects. Experiments demonstrate that our approach is effective in improving the robustness of object-based SLAM in the face of object pose ambiguity.

Consensus-Informed Optimization Over Mixtures for Ambiguity-Aware Object SLAM

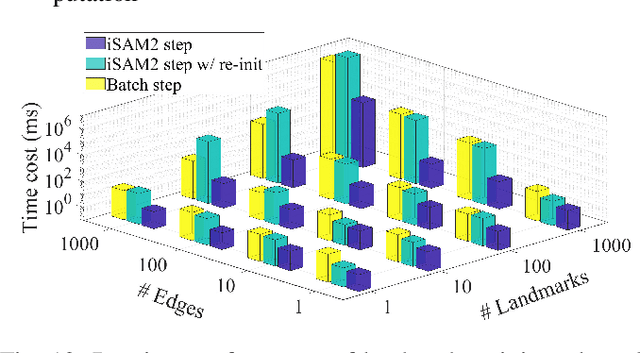
Objects could often have multiple probable poses in single-shot measurements due to symmetry, occlusion or perceptual failures. A robust object-level simultaneous localization and mapping (object SLAM) algorithm needs to be aware of the pose ambiguity. We propose to maintain and subsequently dis-ambiguate the multiple pose interpretations to gradually recover a globally consistent world representation. The max-mixtures model is applied to implicitly and efficiently track all pose hypotheses. The temporally consistent hypotheses are extracted to guide the optimization solution into the global optimum. This consensus-informed inference method is implemented on top of the incremental SLAM framework iSAM2, via landmark variable re-initialization.

Variational Filtering with Copula Models for SLAM

The ability to infer map variables and estimate pose is crucial to the operation of autonomous mobile robots. In most cases the shared dependency between these variables is modeled through a multivariate Gaussian distribution, but there are many situations where that assumption is unrealistic. Our paper shows how it is possible to relax this assumption and perform simultaneous localization and mapping (SLAM) with a larger class of distributions, whose multivariate dependency is represented with a copula model. We integrate the distribution model with copulas into a Sequential Monte Carlo estimator and show how unknown model parameters can be learned through gradient-based optimization. We demonstrate our approach is effective in settings where Gaussian assumptions are clearly violated, such as environments with uncertain data association and nonlinear transition models.

Probabilistic Data Association via Mixture Models for Robust Semantic SLAM

Modern robotic systems sense the environment geometrically, through sensors like cameras, lidar, and sonar, as well as semantically, often through visual models learned from data, such as object detectors. We aim to develop robots that can use all of these sources of information for reliable navigation, but each is corrupted by noise. Rather than assume that object detection will eventually achieve near perfect performance across the lifetime of a robot, in this work we represent and cope with the semantic and geometric uncertainty inherent in methods like object detection. Specifically, we model data association ambiguity, which is typically non-Gaussian, in a way that is amenable to solution within the common nonlinear Gaussian formulation of simultaneous localization and mapping (SLAM). We do so by eliminating data association variables from the inference process through max-marginalization, preserving standard Gaussian posterior assumptions. The result is a max-mixture-type model that accounts for multiple data association hypotheses as well as incorrect loop closures. We provide experimental results on indoor and outdoor semantic navigation tasks with noisy odometry and object detection and find that the ability of the proposed approach to represent multiple hypotheses, including the "null" hypothesis, gives substantial robustness advantages in comparison to alternative semantic SLAM approaches.