An algorithmic solution to the Blotto game using multi-marginal couplings

We describe an efficient algorithm to compute solutions for the general two-player Blotto game on n battlefields with heterogeneous values. While explicit constructions for such solutions have been limited to specific, largely symmetric or homogeneous, setups, this algorithmic resolution covers the most general situation to date: value-asymmetric game with asymmetric budget. The proposed algorithm rests on recent theoretical advances regarding Sinkhorn iterations for matrix and tensor scaling. An important case which had been out of reach of previous attempts is that of heterogeneous but symmetric battlefield values with asymmetric budget. In this case, the Blotto game is constant-sum so optimal solutions exist, and our algorithm samples from an \eps-optimal solution in time O(n^2 + \eps^{-4}), independently of budgets and battlefield values. In the case of asymmetric values where optimal solutions need not exist but Nash equilibria do, our algorithm samples from an \eps-Nash equilibrium with similar complexity but where implicit constants depend on various parameters of the game such as battlefield values.

A probabilistic model for fast-to-evaluate 2D crack path prediction in heterogeneous materials

This paper is devoted to the construction of a new fast-to-evaluate model for the prediction of 2D crack paths in concrete-like microstructures. The model generates piecewise linear cracks paths with segmentation points selected using a Markov chain model. The Markov chain kernel involves local indicators of mechanical interest and its parameters are learnt from numerical full-field 2D simulations of craking using a cohesive-volumetric finite element solver called XPER. The resulting model exhibits a drastic improvement of CPU time in comparison to simulations from XPER.

The query complexity of sampling from strongly log-concave distributions in one dimension

We establish the first tight lower bound of $\Omega(\log\log\kappa)$ on the query complexity of sampling from the class of strongly log-concave and log-smooth distributions with condition number $\kappa$ in one dimension. Whereas existing guarantees for MCMC-based algorithms scale polynomially in $\kappa$, we introduce a novel algorithm based on rejection sampling that closes this doubly exponential gap.

Rejection sampling from shape-constrained distributions in sublinear time

We consider the task of generating exact samples from a target distribution, known up to normalization, over a finite alphabet. The classical algorithm for this task is rejection sampling, and although it has been used in practice for decades, there is surprisingly little study of its fundamental limitations. In this work, we study the query complexity of rejection sampling in a minimax framework for various classes of discrete distributions. Our results provide new algorithms for sampling whose complexity scales sublinearly with the alphabet size. When applied to adversarial bandits, we show that a slight modification of the Exp3 algorithm reduces the per-iteration complexity from $\mathcal O(K)$ to $\mathcal O(\log^2 K)$, where $K$ is the number of arms.

Sampling From the Wasserstein Barycenter

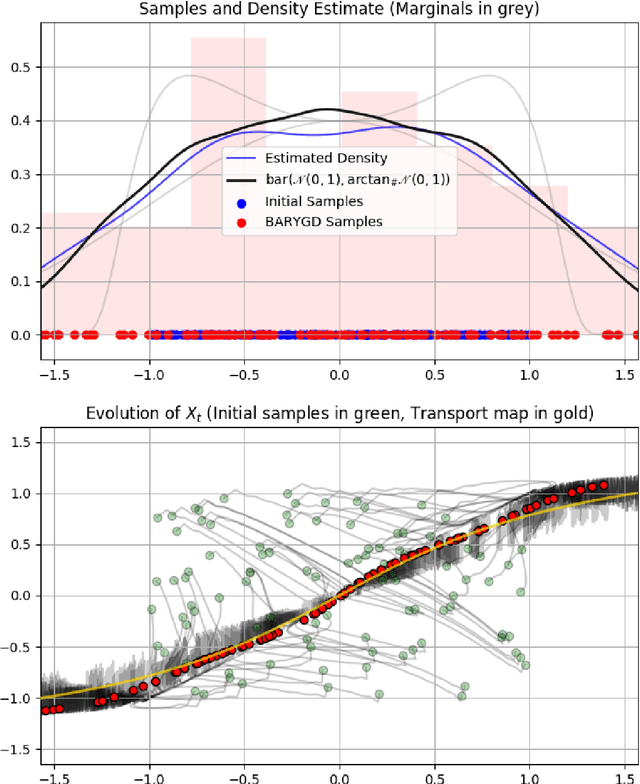
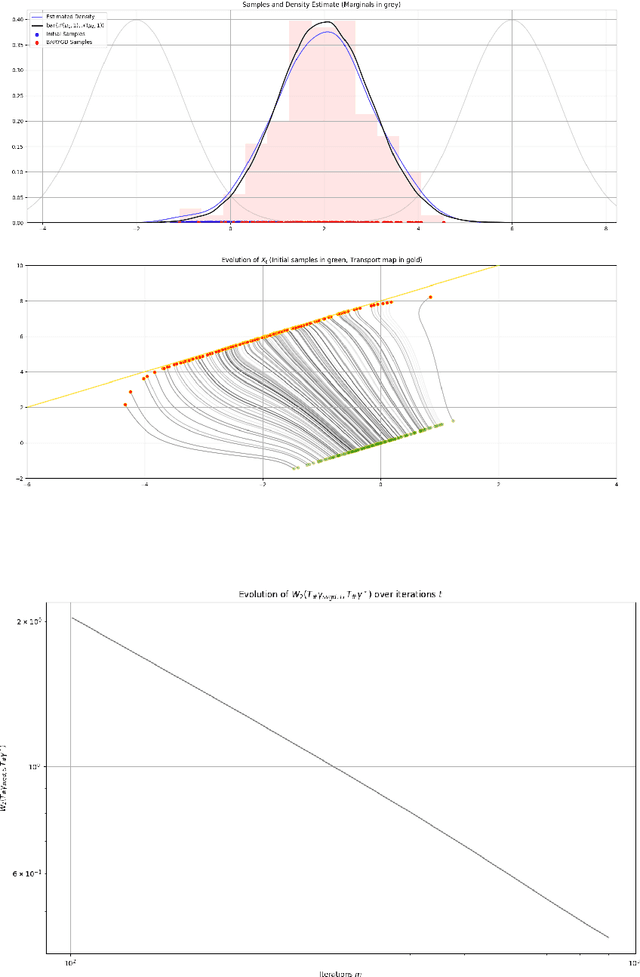
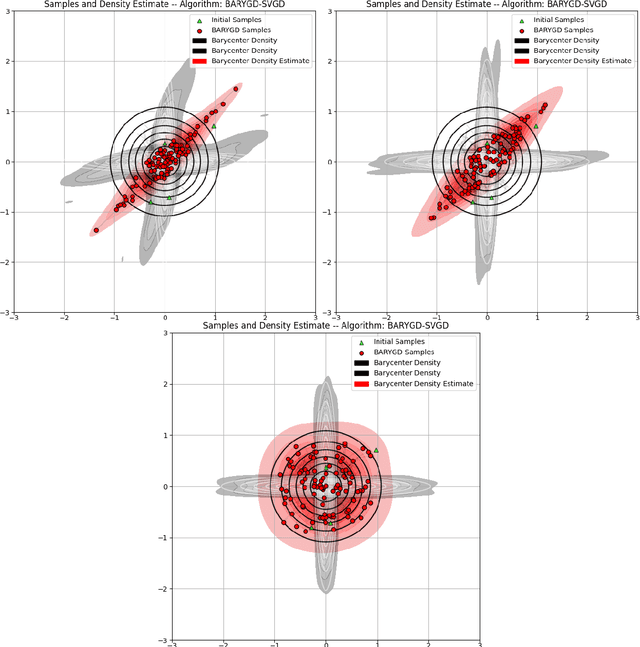
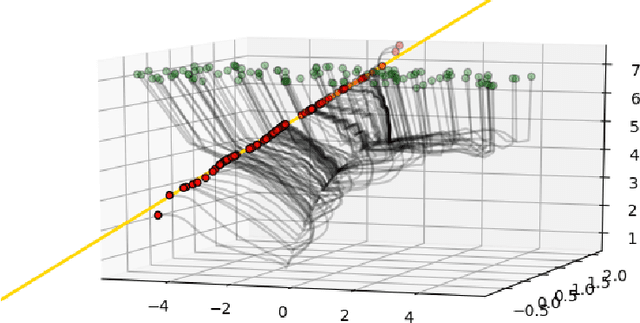
This work presents an algorithm to sample from the Wasserstein barycenter of absolutely continuous measures. Our method is based on the gradient flow of the multimarginal formulation of the Wasserstein barycenter, with an additive penalization to account for the marginal constraints. We prove that the minimum of this penalized multimarginal formulation is achieved for a coupling that is close to the Wasserstein barycenter. The performances of the algorithm are showcased in several settings.

Optimal dimension dependence of the Metropolis-Adjusted Langevin Algorithm

Conventional wisdom in the sampling literature, backed by a popular diffusion scaling limit, suggests that the mixing time of the Metropolis-Adjusted Langevin Algorithm (MALA) scales as $O(d^{1/3})$, where $d$ is the dimension. However, the diffusion scaling limit requires stringent assumptions on the target distribution and is asymptotic in nature. In contrast, the best known non-asymptotic mixing time bound for MALA on the class of log-smooth and strongly log-concave distributions is $O(d)$. In this work, we establish that the mixing time of MALA on this class of target distributions is $\widetilde\Theta(d^{1/2})$ under a warm start. Our upper bound proof introduces a new technique based on a projection characterization of the Metropolis adjustment which reduces the study of MALA to the well-studied discretization analysis of the Langevin SDE and bypasses direct computation of the acceptance probability.

Projection to Fairness in Statistical Learning

In the context of regression, we consider the fundamental question of making an estimator fair while preserving its prediction accuracy as much as possible. To that end, we define its projection to fairness as its closest fair estimator in a sense that reflects prediction accuracy. Our methodology leverages tools from optimal transport to construct efficiently the projection to fairness of any given estimator as a simple post-processing step. Moreover, our approach precisely quantifies the cost of fairness, measured in terms of prediction accuracy.

SVGD as a kernelized Wasserstein gradient flow of the chi-squared divergence

Stein Variational Gradient Descent (SVGD), a popular sampling algorithm, is often described as the kernelized gradient flow for the Kullback-Leibler divergence in the geometry of optimal transport. We introduce a new perspective on SVGD that instead views SVGD as the (kernelized) gradient flow of the chi-squared divergence which, we show, exhibits a strong form of uniform exponential ergodicity under conditions as weak as a Poincar\'e inequality. This perspective leads us to propose an alternative to SVGD, called Laplacian Adjusted Wasserstein Gradient Descent (LAWGD), that can be implemented from the spectral decomposition of the Laplacian operator associated with the target density. We show that LAWGD exhibits strong convergence guarantees and good practical performance.

Exponential ergodicity of mirror-Langevin diffusions

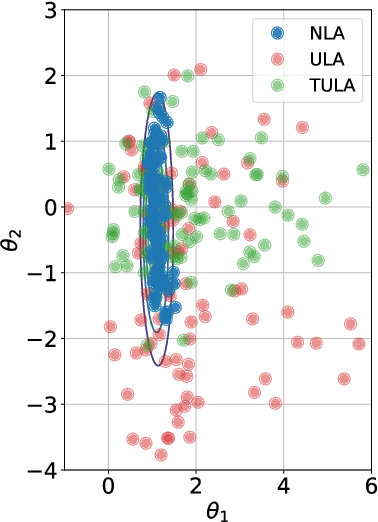
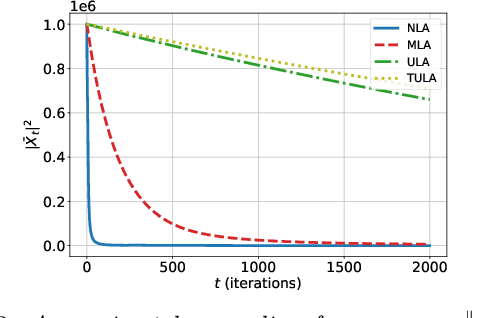
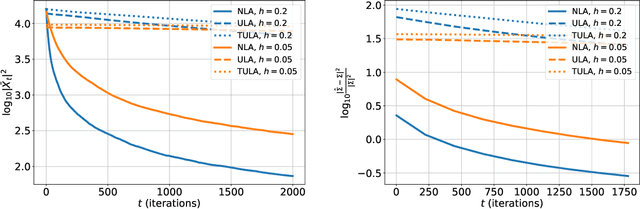
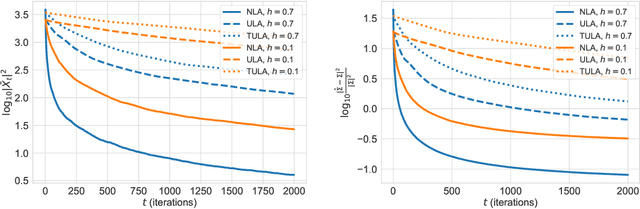
Motivated by the problem of sampling from ill-conditioned log-concave distributions, we give a clean non-asymptotic convergence analysis of mirror-Langevin diffusions as introduced in Zhang et al. (2020). As a special case of this framework, we propose a class of diffusions called Newton-Langevin diffusions and prove that they converge to stationarity exponentially fast with a rate which not only is dimension-free, but also has no dependence on the target distribution. We give an application of this result to the problem of sampling from the uniform distribution on a convex body using a strategy inspired by interior-point methods. Our general approach follows the recent trend of linking sampling and optimization and highlights the role of the chi-squared divergence. In particular, it yields new results on the convergence of the vanilla Langevin diffusion in Wasserstein distance.

A notion of stability for k-means clustering

In this paper, we define and study a new notion of stability for the $k$-means clustering scheme building upon the notion of quantization of a probability measure. We connect this notion of stability to a geometric feature of the underlying distribution of the data, named absolute margin condition, inspired by recent works on the subject.