Minimum intrinsic dimension scaling for entropic optimal transport

Motivated by the manifold hypothesis, which states that data with a high extrinsic dimension may yet have a low intrinsic dimension, we develop refined statistical bounds for entropic optimal transport that are sensitive to the intrinsic dimension of the data. Our bounds involve a robust notion of intrinsic dimension, measured at only a single distance scale depending on the regularization parameter, and show that it is only the minimum of these single-scale intrinsic dimensions which governs the rate of convergence. We call this the Minimum Intrinsic Dimension scaling (MID scaling) phenomenon, and establish MID scaling with no assumptions on the data distributions so long as the cost is bounded and Lipschitz, and for various entropic optimal transport quantities beyond just values, with stronger analogs when one distribution is supported on a manifold. Our results significantly advance the theoretical state of the art by showing that MID scaling is a generic phenomenon, and provide the first rigorous interpretation of the statistical effect of entropic regularization as a distance scale.

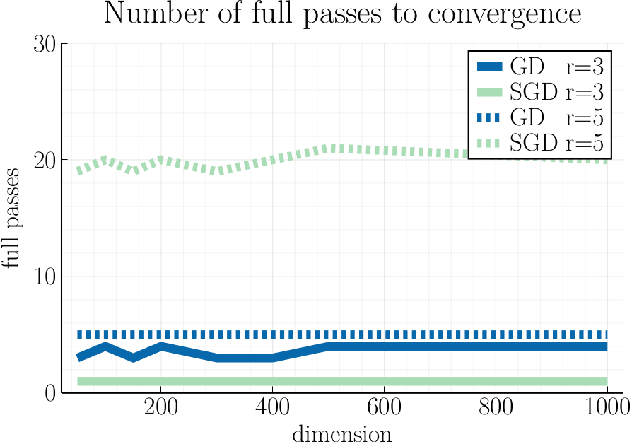
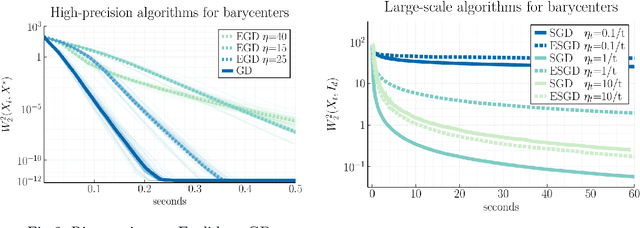
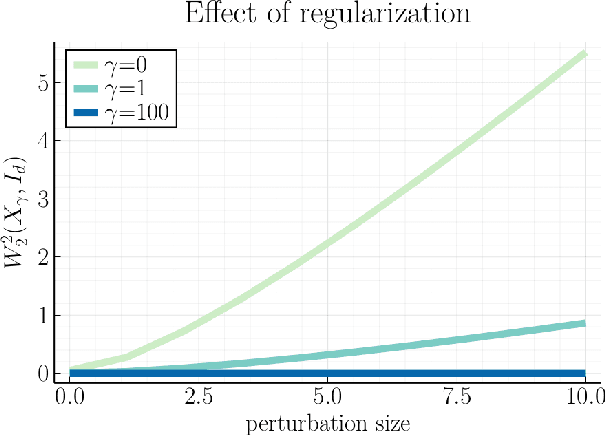
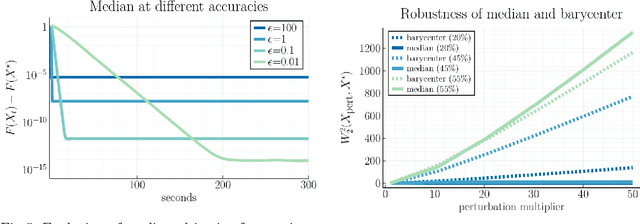
Averaging on the Bures-Wasserstein manifold: dimension-free convergence of gradient descent

We study first-order optimization algorithms for computing the barycenter of Gaussian distributions with respect to the optimal transport metric. Although the objective is geodesically non-convex, Riemannian GD empirically converges rapidly, in fact faster than off-the-shelf methods such as Euclidean GD and SDP solvers. This stands in stark contrast to the best-known theoretical results for Riemannian GD, which depend exponentially on the dimension. In this work, we prove new geodesic convexity results which provide stronger control of the iterates, yielding a dimension-free convergence rate. Our techniques also enable the analysis of two related notions of averaging, the entropically-regularized barycenter and the geometric median, providing the first convergence guarantees for Riemannian GD for these problems.

Exponential ergodicity of mirror-Langevin diffusions

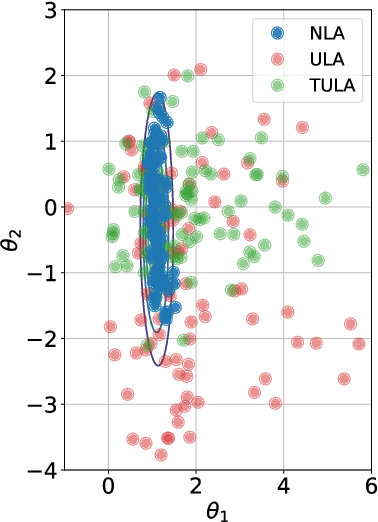
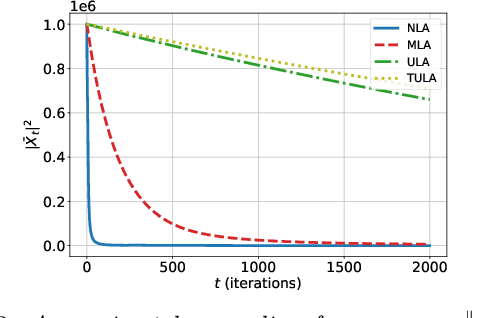
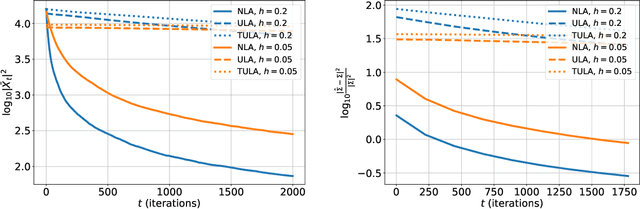
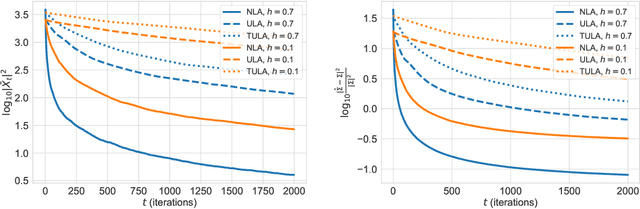
Motivated by the problem of sampling from ill-conditioned log-concave distributions, we give a clean non-asymptotic convergence analysis of mirror-Langevin diffusions as introduced in Zhang et al. (2020). As a special case of this framework, we propose a class of diffusions called Newton-Langevin diffusions and prove that they converge to stationarity exponentially fast with a rate which not only is dimension-free, but also has no dependence on the target distribution. We give an application of this result to the problem of sampling from the uniform distribution on a convex body using a strategy inspired by interior-point methods. Our general approach follows the recent trend of linking sampling and optimization and highlights the role of the chi-squared divergence. In particular, it yields new results on the convergence of the vanilla Langevin diffusion in Wasserstein distance.