Shifted Interpolation for Differential Privacy

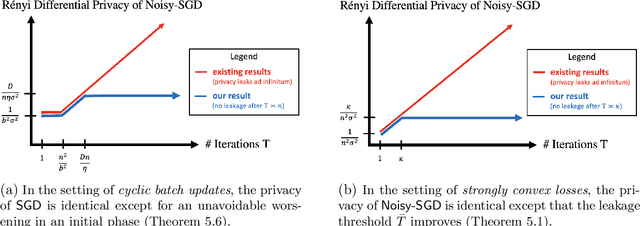
Noisy gradient descent and its variants are the predominant algorithms for differentially private machine learning. It is a fundamental question to quantify their privacy leakage, yet tight characterizations remain open even in the foundational setting of convex losses. This paper improves over previous analyses by establishing (and refining) the "privacy amplification by iteration" phenomenon in the unifying framework of $f$-differential privacy--which tightly captures all aspects of the privacy loss and immediately implies tighter privacy accounting in other notions of differential privacy, e.g., $(\varepsilon,\delta)$-DP and Renyi DP. Our key technical insight is the construction of shifted interpolated processes that unravel the popular shifted-divergences argument, enabling generalizations beyond divergence-based relaxations of DP. Notably, this leads to the first exact privacy analysis in the foundational setting of strongly convex optimization. Our techniques extend to many settings: convex/strongly convex, constrained/unconstrained, full/cyclic/stochastic batches, and all combinations thereof. As an immediate corollary, we recover the $f$-DP characterization of the exponential mechanism for strongly convex optimization in Gopi et al. (2022), and moreover extend this result to more general settings.

Faster high-accuracy log-concave sampling via algorithmic warm starts

Understanding the complexity of sampling from a strongly log-concave and log-smooth distribution $\pi$ on $\mathbb{R}^d$ to high accuracy is a fundamental problem, both from a practical and theoretical standpoint. In practice, high-accuracy samplers such as the classical Metropolis-adjusted Langevin algorithm (MALA) remain the de facto gold standard; and in theory, via the proximal sampler reduction, it is understood that such samplers are key for sampling even beyond log-concavity (in particular, for distributions satisfying isoperimetric assumptions). In this work, we improve the dimension dependence of this sampling problem to $\tilde{O}(d^{1/2})$, whereas the previous best result for MALA was $\tilde{O}(d)$. This closes the long line of work on the complexity of MALA, and moreover leads to state-of-the-art guarantees for high-accuracy sampling under strong log-concavity and beyond (thanks to the aforementioned reduction). Our starting point is that the complexity of MALA improves to $\tilde{O}(d^{1/2})$, but only under a warm start (an initialization with constant R\'enyi divergence w.r.t. $\pi$). Previous algorithms took much longer to find a warm start than to use it, and closing this gap has remained an important open problem in the field. Our main technical contribution settles this problem by establishing the first $\tilde{O}(d^{1/2})$ R\'enyi mixing rates for the discretized underdamped Langevin diffusion. For this, we develop new differential-privacy-inspired techniques based on R\'enyi divergences with Orlicz--Wasserstein shifts, which allow us to sidestep longstanding challenges for proving fast convergence of hypocoercive differential equations.

Concentration of the Langevin Algorithm's Stationary Distribution

A canonical algorithm for log-concave sampling is the Langevin Algorithm, aka the Langevin Diffusion run with some discretization stepsize $\eta > 0$. This discretization leads the Langevin Algorithm to have a stationary distribution $\pi_{\eta}$ which differs from the stationary distribution $\pi$ of the Langevin Diffusion, and it is an important challenge to understand whether the well-known properties of $\pi$ extend to $\pi_{\eta}$. In particular, while concentration properties such as isoperimetry and rapidly decaying tails are classically known for $\pi$, the analogous properties for $\pi_{\eta}$ are open questions with direct algorithmic implications. This note provides a first step in this direction by establishing concentration results for $\pi_{\eta}$ that mirror classical results for $\pi$. Specifically, we show that for any nontrivial stepsize $\eta > 0$, $\pi_{\eta}$ is sub-exponential (respectively, sub-Gaussian) when the potential is convex (respectively, strongly convex). Moreover, the concentration bounds we show are essentially tight. Key to our analysis is the use of a rotation-invariant moment generating function (aka Bessel function) to study the stationary dynamics of the Langevin Algorithm. This technique may be of independent interest because it enables directly analyzing the discrete-time stationary distribution $\pi_{\eta}$ without going through the continuous-time stationary distribution $\pi$ as an intermediary.

Resolving the Mixing Time of the Langevin Algorithm to its Stationary Distribution for Log-Concave Sampling

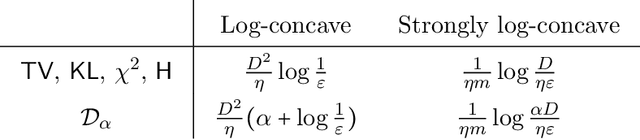
Sampling from a high-dimensional distribution is a fundamental task in statistics, engineering, and the sciences. A particularly canonical approach is the Langevin Algorithm, i.e., the Markov chain for the discretized Langevin Diffusion. This is the sampling analog of Gradient Descent. Despite being studied for several decades in multiple communities, tight mixing bounds for this algorithm remain unresolved even in the seemingly simple setting of log-concave distributions over a bounded domain. This paper completely characterizes the mixing time of the Langevin Algorithm to its stationary distribution in this setting (and others). This mixing result can be combined with any bound on the discretization bias in order to sample from the stationary distribution of the continuous Langevin Diffusion. In this way, we disentangle the study of the mixing and bias of the Langevin Algorithm. Our key insight is to introduce a technique from the differential privacy literature to the sampling literature. This technique, called Privacy Amplification by Iteration, uses as a potential a variant of R\'enyi divergence that is made geometrically aware via Optimal Transport smoothing. This gives a short, simple proof of optimal mixing bounds and has several additional appealing properties. First, our approach removes all unnecessary assumptions required by other sampling analyses. Second, our approach unifies many settings: it extends unchanged if the Langevin Algorithm uses projections, stochastic mini-batch gradients, or strongly convex potentials (whereby our mixing time improves exponentially). Third, our approach exploits convexity only through the contractivity of a gradient step -- reminiscent of how convexity is used in textbook proofs of Gradient Descent. In this way, we offer a new approach towards further unifying the analyses of optimization and sampling algorithms.

Privacy of Noisy Stochastic Gradient Descent: More Iterations without More Privacy Loss

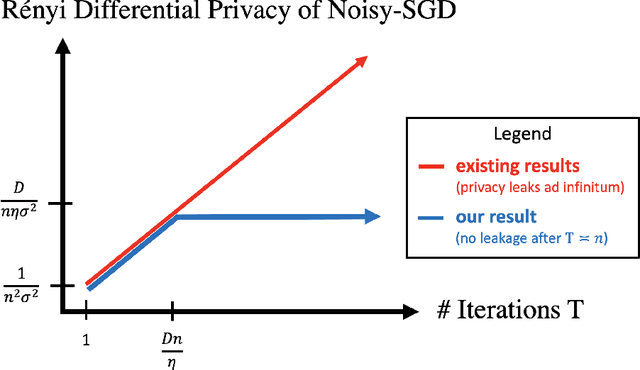
A central issue in machine learning is how to train models on sensitive user data. Industry has widely adopted a simple algorithm: Stochastic Gradient Descent with noise (a.k.a. Stochastic Gradient Langevin Dynamics). However, foundational theoretical questions about this algorithm's privacy loss remain open -- even in the seemingly simple setting of smooth convex losses over a bounded domain. Our main result resolves these questions: for a large range of parameters, we characterize the differential privacy up to a constant factor. This result reveals that all previous analyses for this setting have the wrong qualitative behavior. Specifically, while previous privacy analyses increase ad infinitum in the number of iterations, we show that after a small burn-in period, running SGD longer leaks no further privacy. Our analysis departs completely from previous approaches based on fast mixing, instead using techniques based on optimal transport (namely, Privacy Amplification by Iteration) and the Sampled Gaussian Mechanism (namely, Privacy Amplification by Sampling). Our techniques readily extend to other settings, e.g., strongly convex losses, non-uniform stepsizes, arbitrary batch sizes, and random or cyclic choice of batches.

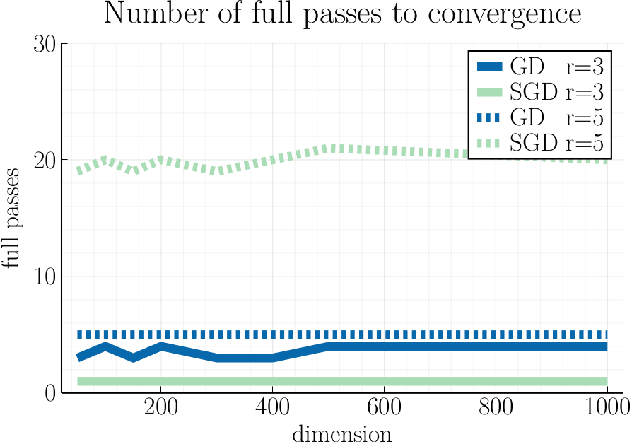
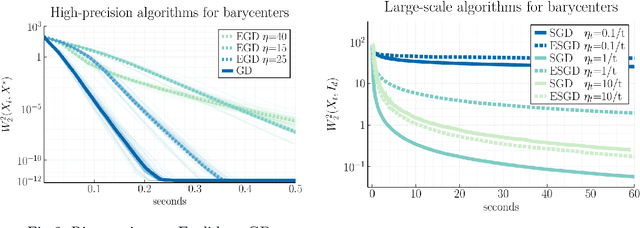
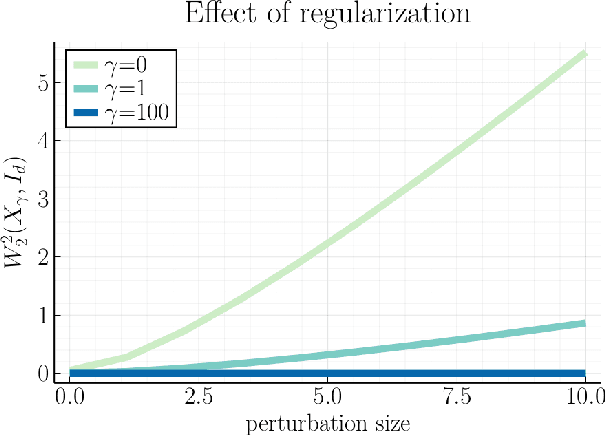
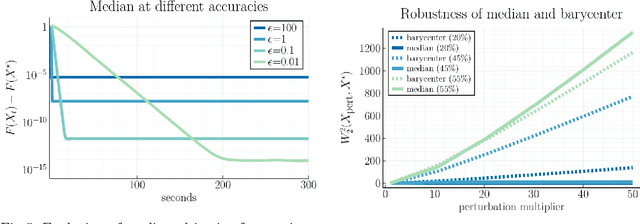
Averaging on the Bures-Wasserstein manifold: dimension-free convergence of gradient descent

We study first-order optimization algorithms for computing the barycenter of Gaussian distributions with respect to the optimal transport metric. Although the objective is geodesically non-convex, Riemannian GD empirically converges rapidly, in fact faster than off-the-shelf methods such as Euclidean GD and SDP solvers. This stands in stark contrast to the best-known theoretical results for Riemannian GD, which depend exponentially on the dimension. In this work, we prove new geodesic convexity results which provide stronger control of the iterates, yielding a dimension-free convergence rate. Our techniques also enable the analysis of two related notions of averaging, the entropically-regularized barycenter and the geometric median, providing the first convergence guarantees for Riemannian GD for these problems.

Kernel approximation on algebraic varieties

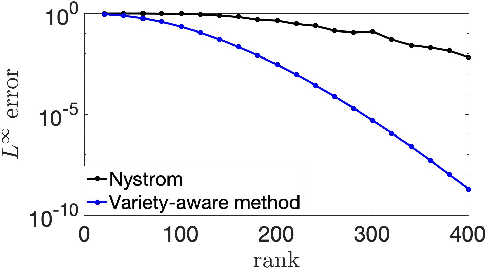
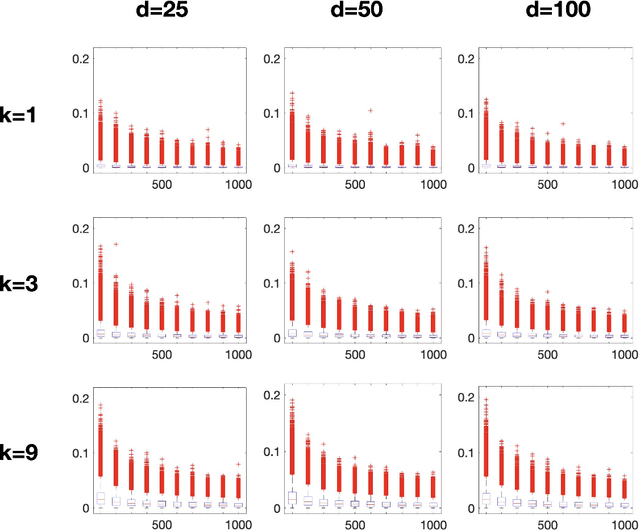
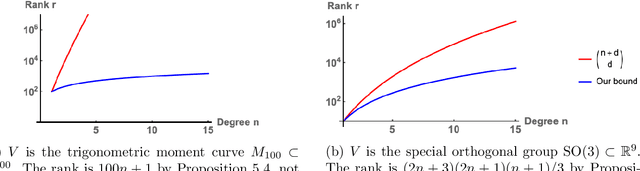
Low-rank approximation of kernels is a fundamental mathematical problem with widespread algorithmic applications. Often the kernel is restricted to an algebraic variety, e.g., in problems involving sparse or low-rank data. We show that significantly better approximations are obtainable in this setting: the rank required to achieve a given error depends on the variety's dimension rather than the ambient dimension, which is typically much larger. This is true in both high-precision and high-dimensional regimes. Our results are presented for smooth isotropic kernels, the predominant class of kernels used in applications. Our main technical insight is to approximate smooth kernels by polynomial kernels, and leverage two key properties of polynomial kernels that hold when they are restricted to a variety. First, their ranks decrease exponentially in the variety's co-dimension. Second, their maximum values are governed by their values over a small set of points. Together, our results provide a general approach for exploiting (approximate) "algebraic structure" in datasets in order to efficiently solve large-scale data science problems.

Wasserstein barycenters are NP-hard to compute

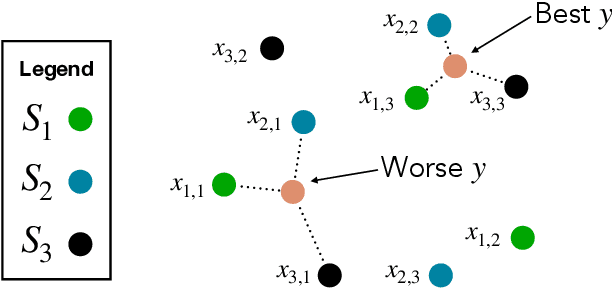
The problem of computing Wasserstein barycenters (a.k.a. Optimal Transport barycenters) has attracted considerable recent attention due to many applications in data science. While there exist polynomial-time algorithms in any fixed dimension, all known runtimes suffer exponentially in the dimension. It is an open question whether this exponential dependence is improvable to a polynomial dependence. This paper proves that unless P=NP, the answer is no. This uncovers a "curse of dimensionality" for Wasserstein barycenter computation which does not occur for Optimal Transport computation. Moreover, our hardness results for computing Wasserstein barycenters extend to approximate computation, to seemingly simple cases of the problem, and to averaging probability distributions in other Optimal Transport metrics.

Hardness results for Multimarginal Optimal Transport problems

Multimarginal Optimal Transport (MOT) is the problem of linear programming over joint probability distributions with fixed marginals. A key issue in many applications is the complexity of solving MOT: the linear program has exponential size in the number of marginals k and their support sizes n. A recent line of work has shown that MOT is poly(n,k)-time solvable for certain families of costs that have poly(n,k)-size implicit representations. However, it is unclear what further families of costs this line of algorithmic research can encompass. In order to understand these fundamental limitations, this paper initiates the study of intractability results for MOT. Our main technical contribution is developing a toolkit for proving NP-hardness and inapproximability results for MOT problems. We demonstrate this toolkit by using it to establish the intractability of a number of MOT problems studied in the literature that have resisted previous algorithmic efforts. For instance, we provide evidence that repulsive costs make MOT intractable by showing that several such problems of interest are NP-hard to solve--even approximately.

Polynomial-time algorithms for Multimarginal Optimal Transport problems with structure

Multimarginal Optimal Transport (MOT) has recently attracted significant interest due to its many applications. However, in most applications, the success of MOT is severely hindered by a lack of sub-exponential time algorithms. This paper develops a general theory about "structural properties" that make MOT tractable. We identify two such properties: decomposability of the cost into either (i) local interactions and simple global interactions; or (ii) low-rank interactions and sparse interactions. We also provide strong evidence that (iii) repulsive costs make MOT intractable by showing that several such problems of interest are NP-hard to solve--even approximately. These three structures are quite general, and collectively they encompass many (if not most) current MOT applications. We demonstrate our results on a variety of applications in machine learning, statistics, physics, and computational geometry.