Acceleration and Implicit Regularization in Gaussian Phase Retrieval

We study accelerated optimization methods in the Gaussian phase retrieval problem. In this setting, we prove that gradient methods with Polyak or Nesterov momentum have similar implicit regularization to gradient descent. This implicit regularization ensures that the algorithms remain in a nice region, where the cost function is strongly convex and smooth despite being nonconvex in general. This ensures that these accelerated methods achieve faster rates of convergence than gradient descent. Experimental evidence demonstrates that the accelerated methods converge faster than gradient descent in practice.

Eikonal depth: an optimal control approach to statistical depths

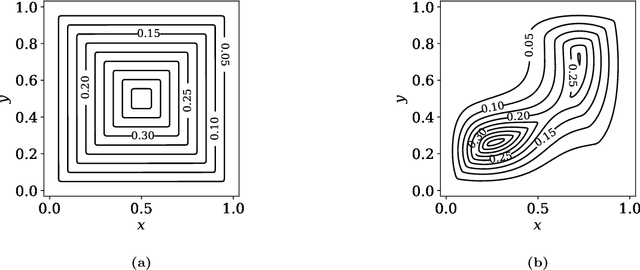
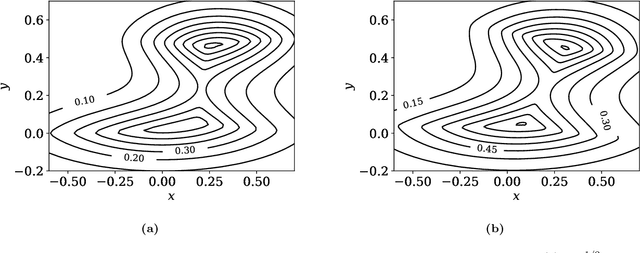
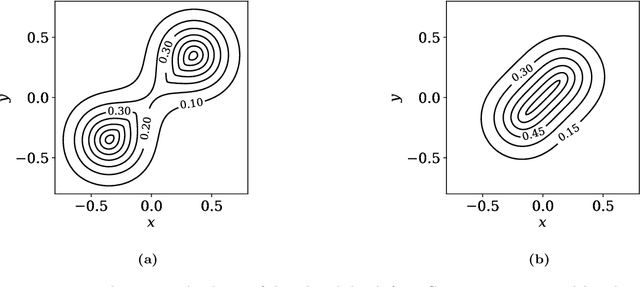
Statistical depths provide a fundamental generalization of quantiles and medians to data in higher dimensions. This paper proposes a new type of globally defined statistical depth, based upon control theory and eikonal equations, which measures the smallest amount of probability density that has to be passed through in a path to points outside the support of the distribution: for example spatial infinity. This depth is easy to interpret and compute, expressively captures multi-modal behavior, and extends naturally to data that is non-Euclidean. We prove various properties of this depth, and provide discussion of computational considerations. In particular, we demonstrate that this notion of depth is robust under an aproximate isometrically constrained adversarial model, a property which is not enjoyed by the Tukey depth. Finally we give some illustrative examples in the context of two-dimensional mixture models and MNIST.

Tukey Depths and Hamilton-Jacobi Differential Equations

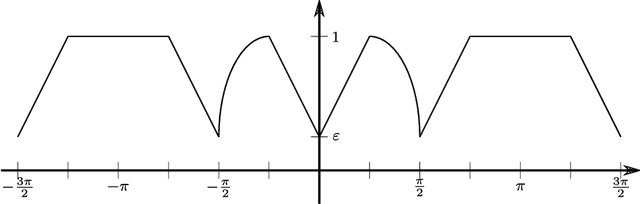
The widespread application of modern machine learning has increased the need for robust statistical algorithms. This work studies one such fundamental statistical measure known as the Tukey depth. We study the problem in the continuum (population) limit. In particular, we derive the associated necessary conditions, which take the form of a first-order partial differential equation. We discuss the classical interpretation of this necessary condition as the viscosity solution of a Hamilton-Jacobi equation, but with a non-classical Hamiltonian with discontinuous dependence on the gradient at zero. We prove that this equation possesses a unique viscosity solution and that this solution always bounds the Tukey depth from below. In certain cases, we prove that the Tukey depth is equal to the viscosity solution, and we give some illustrations of standard numerical methods from the optimal control community which deal directly with the partial differential equation. We conclude by outlining several promising research directions both in terms of new numerical algorithms and theoretical challenges.