Tukey Depths and Hamilton-Jacobi Differential Equations
Paper and Code
Apr 04, 2021
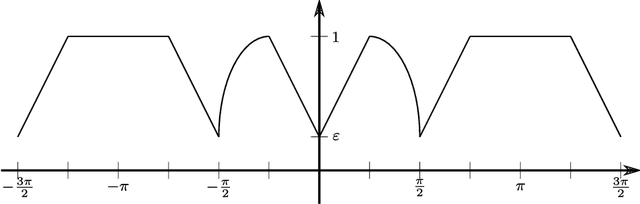
The widespread application of modern machine learning has increased the need for robust statistical algorithms. This work studies one such fundamental statistical measure known as the Tukey depth. We study the problem in the continuum (population) limit. In particular, we derive the associated necessary conditions, which take the form of a first-order partial differential equation. We discuss the classical interpretation of this necessary condition as the viscosity solution of a Hamilton-Jacobi equation, but with a non-classical Hamiltonian with discontinuous dependence on the gradient at zero. We prove that this equation possesses a unique viscosity solution and that this solution always bounds the Tukey depth from below. In certain cases, we prove that the Tukey depth is equal to the viscosity solution, and we give some illustrations of standard numerical methods from the optimal control community which deal directly with the partial differential equation. We conclude by outlining several promising research directions both in terms of new numerical algorithms and theoretical challenges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge