A Subspace-Constrained Tyler's Estimator and its Applications to Structure from Motion
Paper and Code
Apr 17, 2024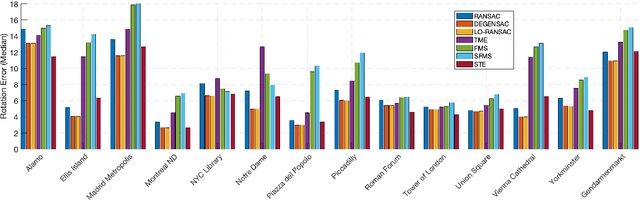
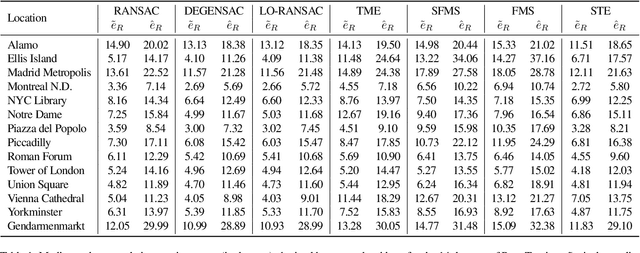
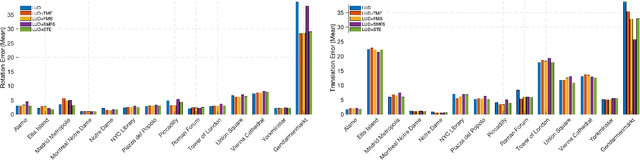
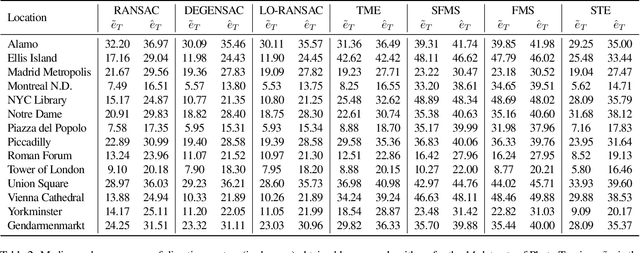
We present the subspace-constrained Tyler's estimator (STE) designed for recovering a low-dimensional subspace within a dataset that may be highly corrupted with outliers. STE is a fusion of the Tyler's M-estimator (TME) and a variant of the fast median subspace. Our theoretical analysis suggests that, under a common inlier-outlier model, STE can effectively recover the underlying subspace, even when it contains a smaller fraction of inliers relative to other methods in the field of robust subspace recovery. We apply STE in the context of Structure from Motion (SfM) in two ways: for robust estimation of the fundamental matrix and for the removal of outlying cameras, enhancing the robustness of the SfM pipeline. Numerical experiments confirm the state-of-the-art performance of our method in these applications. This research makes significant contributions to the field of robust subspace recovery, particularly in the context of computer vision and 3D reconstruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge