Neural Conjugate Flows: Physics-informed architectures with flow structure

We introduce Neural Conjugate Flows (NCF), a class of neural network architectures equipped with exact flow structure. By leveraging topological conjugation, we prove that these networks are not only naturally isomorphic to a continuous group, but are also universal approximators for flows of ordinary differential equation (ODEs). Furthermore, topological properties of these flows can be enforced by the architecture in an interpretable manner. We demonstrate in numerical experiments how this topological group structure leads to concrete computational gains over other physics informed neural networks in estimating and extrapolating latent dynamics of ODEs, while training up to five times faster than other flow-based architectures.

SelfReDepth: Self-Supervised Real-Time Depth Restoration for Consumer-Grade Sensors

Depth maps produced by consumer-grade sensors suffer from inaccurate measurements and missing data from either system or scene-specific sources. Data-driven denoising algorithms can mitigate such problems. However, they require vast amounts of ground truth depth data. Recent research has tackled this limitation using self-supervised learning techniques, but it requires multiple RGB-D sensors. Moreover, most existing approaches focus on denoising single isolated depth maps or specific subjects of interest, highlighting a need for methods to effectively denoise depth maps in real-time dynamic environments. This paper extends state-of-the-art approaches for depth-denoising commodity depth devices, proposing SelfReDepth, a self-supervised deep learning technique for depth restoration, via denoising and hole-filling by inpainting full-depth maps captured with RGB-D sensors. The algorithm targets depth data in video streams, utilizing multiple sequential depth frames coupled with color data to achieve high-quality depth videos with temporal coherence. Finally, SelfReDepth is designed to be compatible with various RGB-D sensors and usable in real-time scenarios as a pre-processing step before applying other depth-dependent algorithms. Our results demonstrate our approach's real-time performance on real-world datasets. They show that it outperforms state-of-the-art denoising and restoration performance at over 30fps on Commercial Depth Cameras, with potential benefits for augmented and mixed-reality applications.

Tensor Moments of Gaussian Mixture Models: Theory and Applications

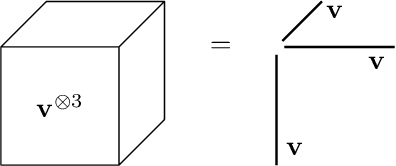
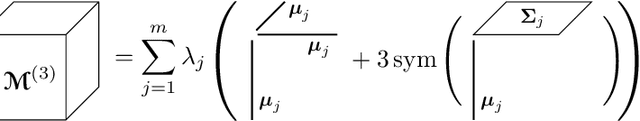
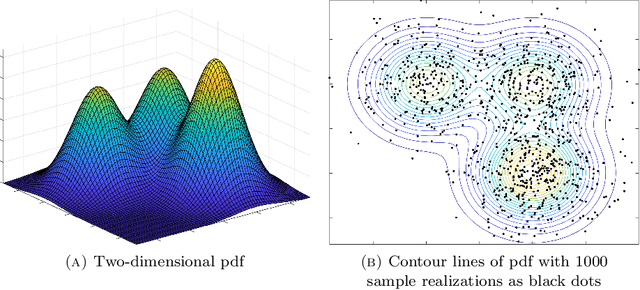
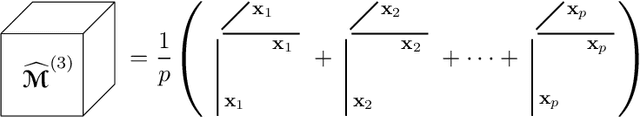
Gaussian mixture models (GMM) are fundamental tools in statistical and data sciences. We study the moments of multivariate Gaussians and GMMs. The $d$-th moment of an $n$-dimensional random variable is a symmetric $d$-way tensor of size $n^d$, so working with moments naively is assumed to be prohibitively expensive for $d>2$ and larger values of $n$. In this work, we develop theory and numerical methods for implicit computations with moment tensors of GMMs, reducing the computational and storage costs to $\mathcal{O}(n^2)$ and $\mathcal{O}(n^3)$, respectively, for general covariance matrices, and to $\mathcal{O}(n)$ and $\mathcal{O}(n)$, respectively, for diagonal ones. We derive concise analytic expressions for the moments in terms of symmetrized tensor products, relying on the correspondence between symmetric tensors and homogeneous polynomials, and combinatorial identities involving Bell polynomials. The primary application of this theory is to estimating GMM parameters from a set of observations, when formulated as a moment-matching optimization problem. If there is a known and common covariance matrix, we also show it is possible to debias the data observations, in which case the problem of estimating the unknown means reduces to symmetric CP tensor decomposition. Numerical results validate and illustrate the numerical efficiency of our approaches. This work potentially opens the door to the competitiveness of the method of moments as compared to expectation maximization methods for parameter estimation of GMMs.

Landscape analysis of an improved power method for tensor decomposition

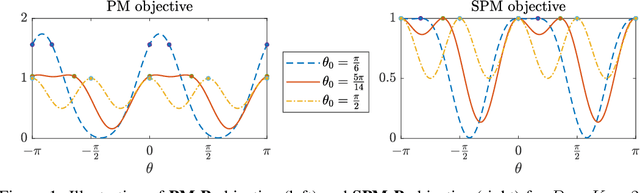
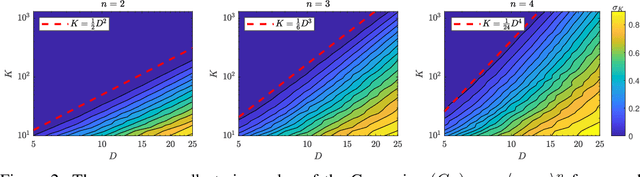
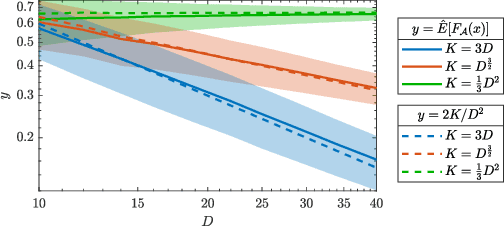
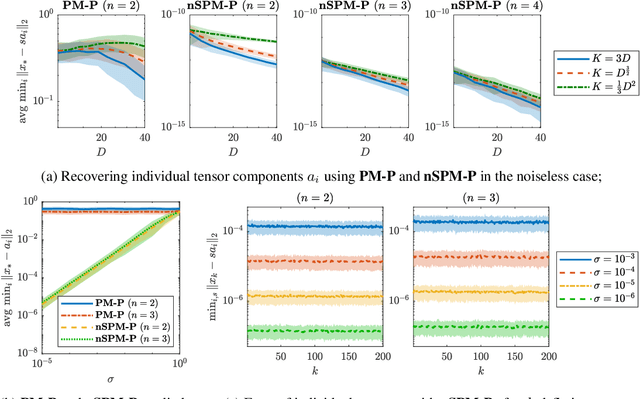
In this work, we consider the optimization formulation for symmetric tensor decomposition recently introduced in the Subspace Power Method (SPM) of Kileel and Pereira. Unlike popular alternative functionals for tensor decomposition, the SPM objective function has the desirable properties that its maximal value is known in advance, and its global optima are exactly the rank-1 components of the tensor when the input is sufficiently low-rank. We analyze the non-convex optimization landscape associated with the SPM objective. Our analysis accounts for working with noisy tensors. We derive quantitative bounds such that any second-order critical point with SPM objective value exceeding the bound must equal a tensor component in the noiseless case, and must approximate a tensor component in the noisy case. For decomposing tensors of size $D^{\times m}$, we obtain a near-global guarantee up to rank $\widetilde{o}(D^{\lfloor m/2 \rfloor})$ under a random tensor model, and a global guarantee up to rank $\mathcal{O}(D)$ assuming deterministic frame conditions. This implies that SPM with suitable initialization is a provable, efficient, robust algorithm for low-rank symmetric tensor decomposition. We conclude with numerics that show a practical preferability for using the SPM functional over a more established counterpart.

Learning latent stochastic differential equations with variational auto-encoders

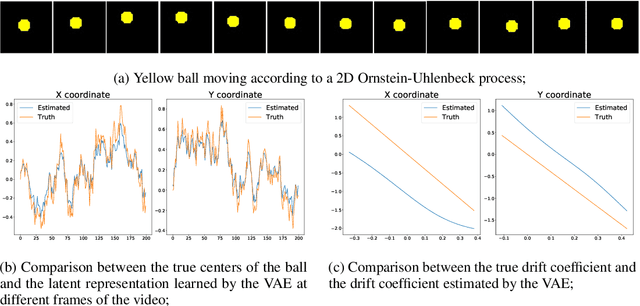
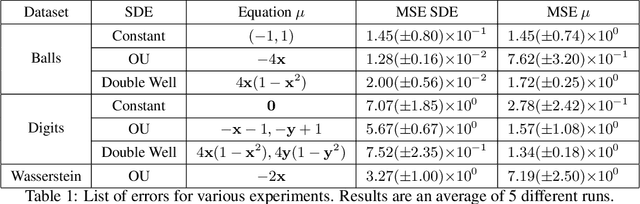
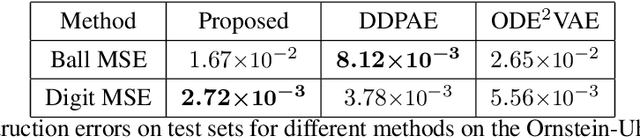
We present a method for learning latent stochastic differential equations (SDEs) from high dimensional time series data. Given a time series generated from a lower dimensional It\^{o} process, the proposed method uncovers the relevant parameters of the SDE through a self-supervised learning approach. Using the framework of variational autoencoders (VAEs), we consider a conditional generative model for the data based on the Euler-Maruyama approximation of SDE solutions. Furthermore, we use recent results on identifiability of semi-supervised learning to show that our model can recover not only the underlying SDE parameters, but also the original latent space, up to an isometry, in the limit of infinite data. We validate the model through a series of different simulated video processing tasks where the underlying SDE is known. Our results suggest that the proposed method effectively learns the underlying SDE, as predicted by the theory.

Robust Marine Buoy Placement for Ship Detection Using Dropout K-Means

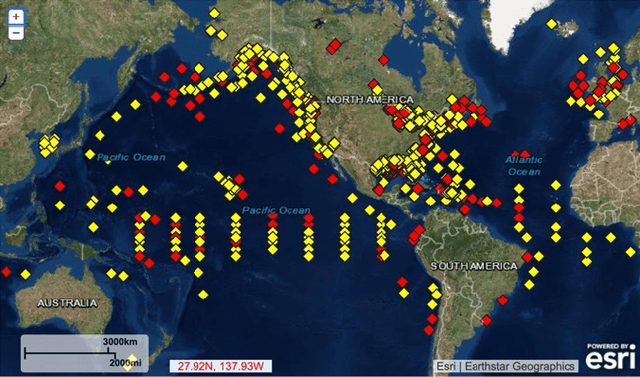
Marine buoys aid in the battle against Illegal, Unreported and Unregulated (IUU) fishing by detecting fishing vessels in their vicinity. Marine buoys, however, may be disrupted by natural causes and buoy vandalism. In this paper, we formulate marine buoy placement as a clustering problem, and propose dropout k-means and dropout k-median to improve placement robustness to buoy disruption. We simulated the passage of ships in the Gabonese waters near West Africa using historical Automatic Identification System (AIS) data, then compared the ship detection probability of dropout k-means to classic k-means and dropout k-median to classic k-median. With 5 buoys, the buoy arrangement computed by classic k-means, dropout k-means, classic k-median and dropout k-median have ship detection probabilities of 38%, 45%, 48% and 52%.

Learning Partial Differential Equations from Data Using Neural Networks

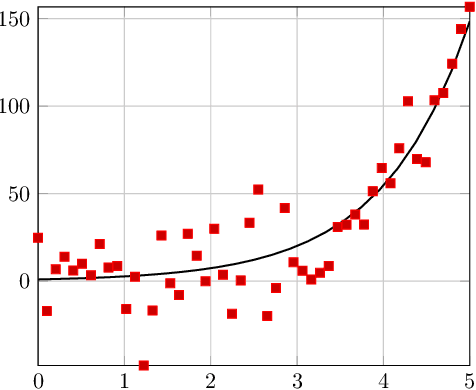
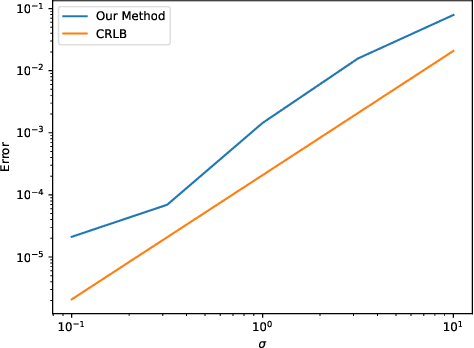
We develop a framework for estimating unknown partial differential equations from noisy data, using a deep learning approach. Given noisy samples of a solution to an unknown PDE, our method interpolates the samples using a neural network, and extracts the PDE by equating derivatives of the neural network approximation. Our method applies to PDEs which are linear combinations of user-defined dictionary functions, and generalizes previous methods that only consider parabolic PDEs. We introduce a regularization scheme that prevents the function approximation from overfitting the data and forces it to be a solution of the underlying PDE. We validate the model on simulated data generated by the known PDEs and added Gaussian noise, and we study our method under different levels of noise. We also compare the error of our method with a Cramer-Rao lower bound for an ordinary differential equation. Our results indicate that our method outperforms other methods in estimating PDEs, especially in the low signal-to-noise regime.