Neural Architecture Search From Fréchet Task Distance

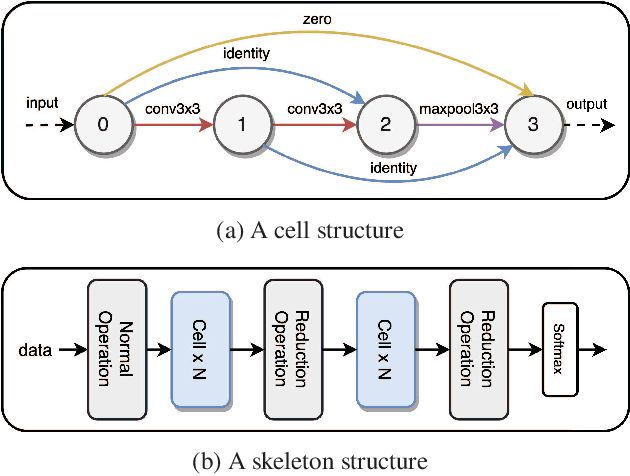
We formulate a Fr\'echet-type asymmetric distance between tasks based on Fisher Information Matrices. We show how the distance between a target task and each task in a given set of baseline tasks can be used to reduce the neural architecture search space for the target task. The complexity reduction in search space for task-specific architectures is achieved by building on the optimized architectures for similar tasks instead of doing a full search without using this side information. Experimental results demonstrate the efficacy of the proposed approach and its improvements over the state-of-the-art methods.

Neural Architecture Search From Task Similarity Measure

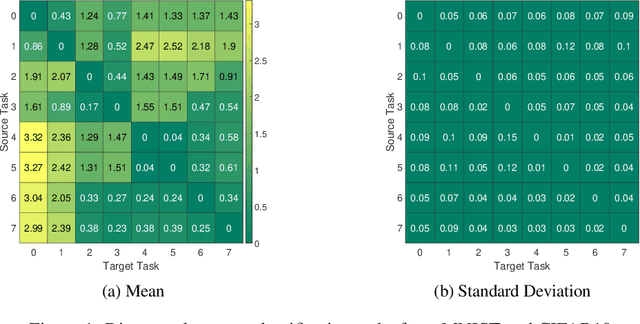
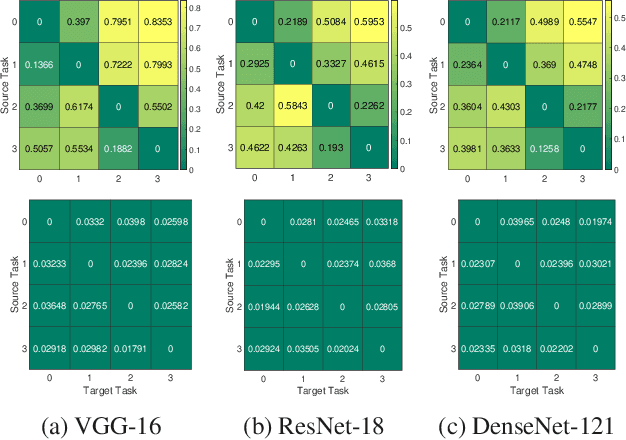
In this paper, we propose a neural architecture search framework based on a similarity measure between various tasks defined in terms of Fisher information. By utilizing the relation between a target and a set of existing tasks, the search space of architectures can be significantly reduced, making the discovery of the best candidates in the set of possible architectures tractable. This method eliminates the requirement for training the networks from scratch for the target task. Simulation results illustrate the efficacy of our proposed approach and its competitiveness with state-of-the-art methods.

Task-Aware Neural Architecture Search

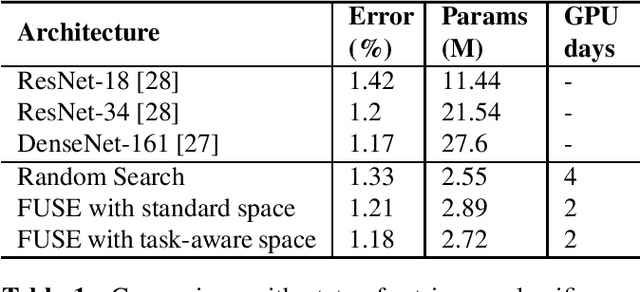
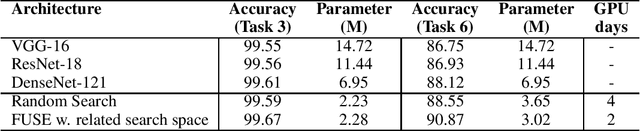
The design of handcrafted neural networks requires a lot of time and resources. Recent techniques in Neural Architecture Search (NAS) have proven to be competitive or better than traditional handcrafted design, although they require domain knowledge and have generally used limited search spaces. In this paper, we propose a novel framework for neural architecture search, utilizing a dictionary of models of base tasks and the similarity between the target task and the atoms of the dictionary; hence, generating an adaptive search space based on the base models of the dictionary. By introducing a gradient-based search algorithm, we can evaluate and discover the best architecture in the search space without fully training the networks. The experimental results show the efficacy of our proposed task-aware approach.

Approximating the Riemannian Metric from Point Clouds via Manifold Moving Least Squares

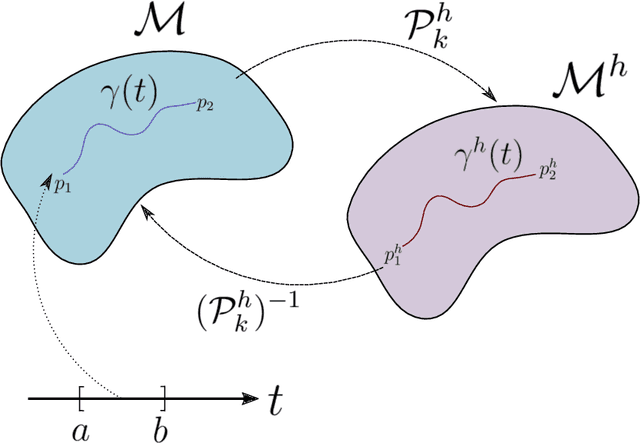
The approximation of both geodesic distances and shortest paths on point cloud sampled from an embedded submanifold $\mathcal{M}$ of Euclidean space has been a long-standing challenge in computational geometry. Given a sampling resolution parameter $ h $, state-of-the-art discrete methods yield $ O(h^2) $ approximations at most. In this paper, we investigate the convergence of such approximations made by Manifold Moving Least-Squares (Manifold-MLS), a method that constructs an approximating manifold $\mathcal{M}^h$ using information from a given point cloud that was developed by Sober \& Levin in 2019 . They showed that the Manifold-MLS procedure approximates the original manifold with approximation order of $ O(h^{k})$ provided that the original manifold $\mathcal{M} \in C^{k}$ is closed, i.e. $\mathcal{M}$ is a compact manifold without boundary. In this paper, we show that under the same conditions, the Riemannian metric of $ \mathcal{M}^h $ approximates the Riemannian metric of $ \mathcal{M}, $; i.e., $\mathcal{M}$ is nearly isometric to $\mathcal{M}^h$. Explicitly, given points $ p_1, p_2 \in \mathcal{M} $ with geodesic distance $ \rho_{\mathcal{M}}(p_1, p_2) $, we show that their corresponding points $ p_1^h, p_2^h \in \mathcal{M}^h $ have a geodesic distance of $ \rho_{\mathcal{M}^h}(p_1^h,p_2^h) = \rho_{\mathcal{M}}(p_1, p_2) + O(h^{k-1}) $. We then use this result, as well as the fact that $ \mathcal{M}^h $ can be sampled with any desired resolution, to devise a naive algorithm that yields approximate geodesic distances with rate of convergence $ O(h^{k-1}) $. We show the potential and the robustness to noise of the proposed method on some numerical simulations.

Learning Partial Differential Equations from Data Using Neural Networks

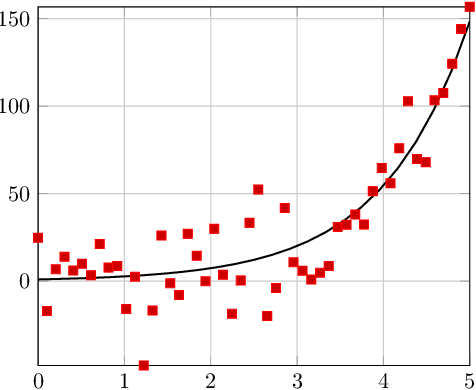
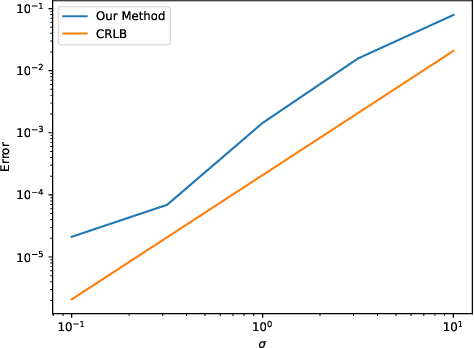
We develop a framework for estimating unknown partial differential equations from noisy data, using a deep learning approach. Given noisy samples of a solution to an unknown PDE, our method interpolates the samples using a neural network, and extracts the PDE by equating derivatives of the neural network approximation. Our method applies to PDEs which are linear combinations of user-defined dictionary functions, and generalizes previous methods that only consider parabolic PDEs. We introduce a regularization scheme that prevents the function approximation from overfitting the data and forces it to be a solution of the underlying PDE. We validate the model on simulated data generated by the known PDEs and added Gaussian noise, and we study our method under different levels of noise. We also compare the error of our method with a Cramer-Rao lower bound for an ordinary differential equation. Our results indicate that our method outperforms other methods in estimating PDEs, especially in the low signal-to-noise regime.