Approximating the Riemannian Metric from Point Clouds via Manifold Moving Least Squares

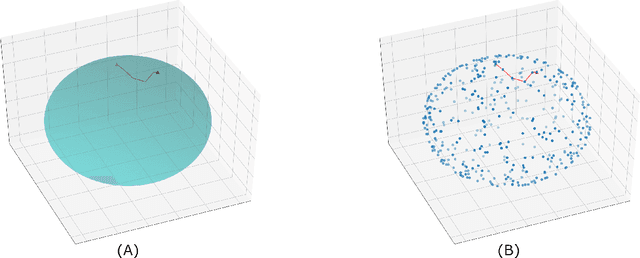
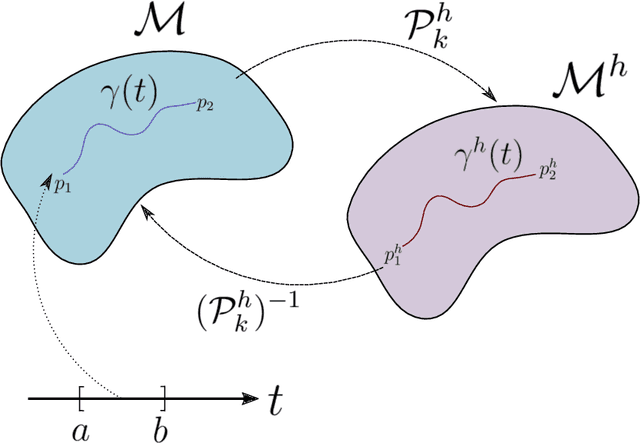
The approximation of both geodesic distances and shortest paths on point cloud sampled from an embedded submanifold $\mathcal{M}$ of Euclidean space has been a long-standing challenge in computational geometry. Given a sampling resolution parameter $ h $, state-of-the-art discrete methods yield $ O(h^2) $ approximations at most. In this paper, we investigate the convergence of such approximations made by Manifold Moving Least-Squares (Manifold-MLS), a method that constructs an approximating manifold $\mathcal{M}^h$ using information from a given point cloud that was developed by Sober \& Levin in 2019 . They showed that the Manifold-MLS procedure approximates the original manifold with approximation order of $ O(h^{k})$ provided that the original manifold $\mathcal{M} \in C^{k}$ is closed, i.e. $\mathcal{M}$ is a compact manifold without boundary. In this paper, we show that under the same conditions, the Riemannian metric of $ \mathcal{M}^h $ approximates the Riemannian metric of $ \mathcal{M}, $; i.e., $\mathcal{M}$ is nearly isometric to $\mathcal{M}^h$. Explicitly, given points $ p_1, p_2 \in \mathcal{M} $ with geodesic distance $ \rho_{\mathcal{M}}(p_1, p_2) $, we show that their corresponding points $ p_1^h, p_2^h \in \mathcal{M}^h $ have a geodesic distance of $ \rho_{\mathcal{M}^h}(p_1^h,p_2^h) = \rho_{\mathcal{M}}(p_1, p_2) + O(h^{k-1}) $. We then use this result, as well as the fact that $ \mathcal{M}^h $ can be sampled with any desired resolution, to devise a naive algorithm that yields approximate geodesic distances with rate of convergence $ O(h^{k-1}) $. We show the potential and the robustness to noise of the proposed method on some numerical simulations.