Clifford Spiegelman
Semiparametric Classification of Forest Graphical Models
Jun 06, 2018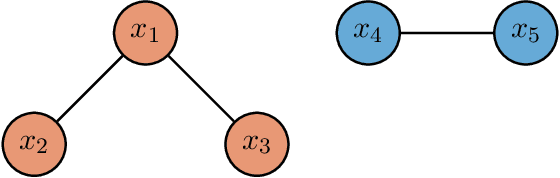

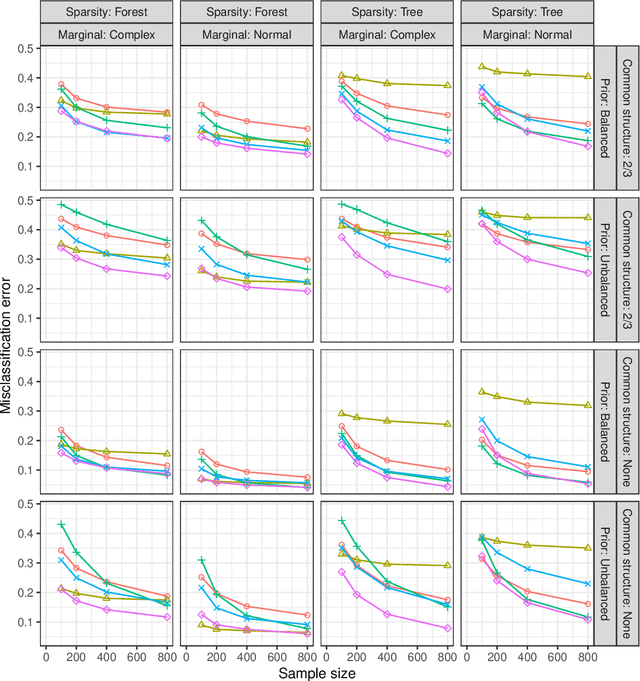
Abstract:We propose a new semiparametric approach to binary classification that exploits the modeling flexibility of sparse graphical models. Specifically, we assume that each class can be represented by a forest-structured graphical model. Under this assumption, the optimal classifier is linear in the log of the one- and two-dimensional marginal densities. Our proposed procedure non-parametrically estimates the univariate and bivariate marginal densities, maps each sample to the logarithm of these estimated densities and constructs a linear SVM in the transformed space. We prove convergence of the resulting classifier to an oracle SVM classifier and give finite sample bounds on its excess risk. Experiments with simulated and real data indicate that the resulting classifier is competitive with several popular methods across a range of applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge