Manifold learning with arbitrary norms

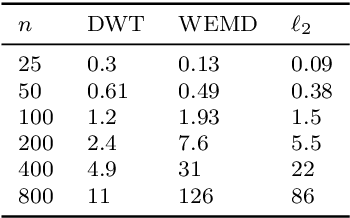
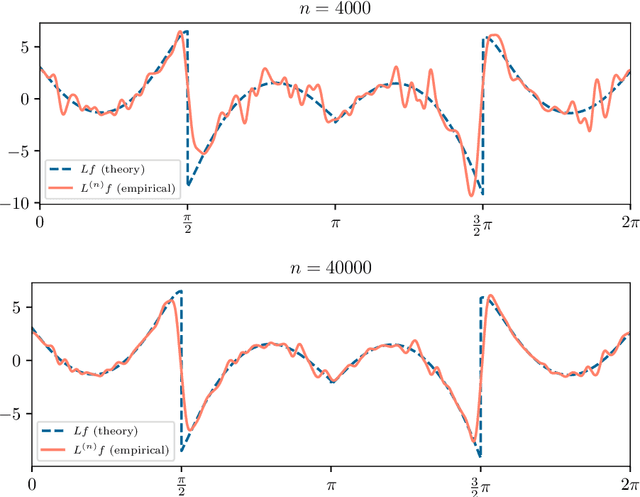
Manifold learning methods play a prominent role in nonlinear dimensionality reduction and other tasks involving high-dimensional data sets with low intrinsic dimensionality. Many of these methods are graph-based: they associate a vertex with each data point and a weighted edge between each pair of close points. Existing theory shows, under certain conditions, that the Laplacian matrix of the constructed graph converges to the Laplace-Beltrami operator of the data manifold. However, this result assumes the Euclidean norm is used for measuring distances. In this paper, we determine the limiting differential operator for graph Laplacians constructed using $\textit{any}$ norm. The proof involves a subtle interplay between the second fundamental form of the underlying manifold and the convex geometry of the norm's unit ball. To motivate the use of non-Euclidean norms, we show in a numerical simulation that manifold learning based on Earthmover's distances outperforms the standard Euclidean variant for learning molecular shape spaces, in terms of both sample complexity and computational complexity.

Earthmover-based manifold learning for analyzing molecular conformation spaces

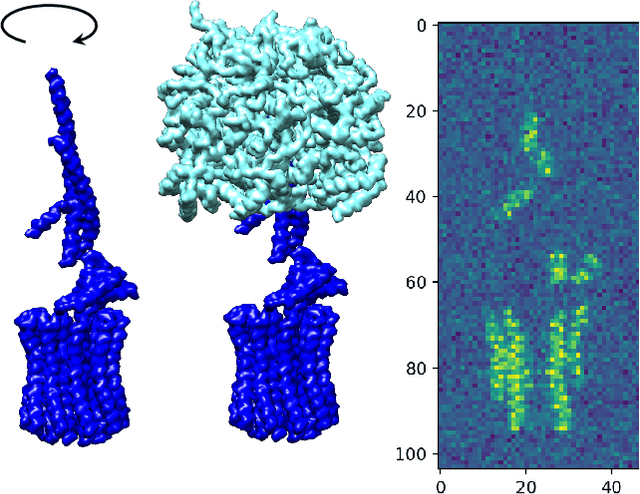
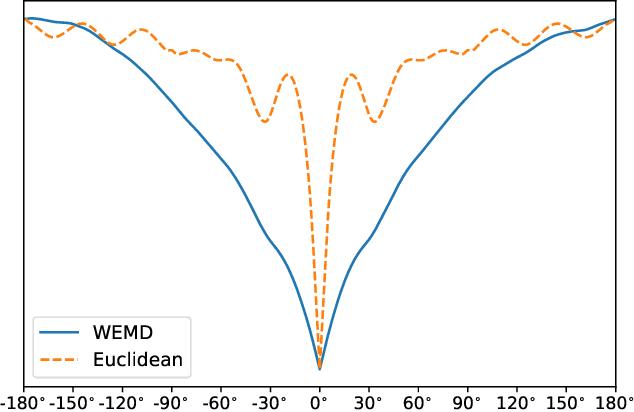
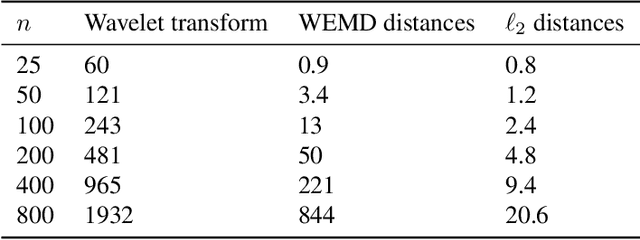
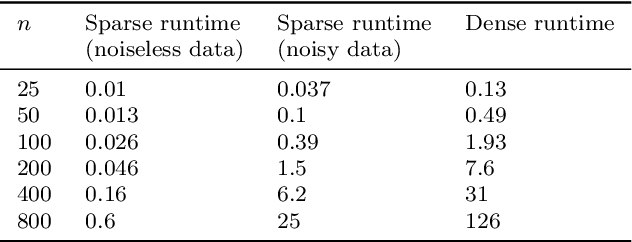
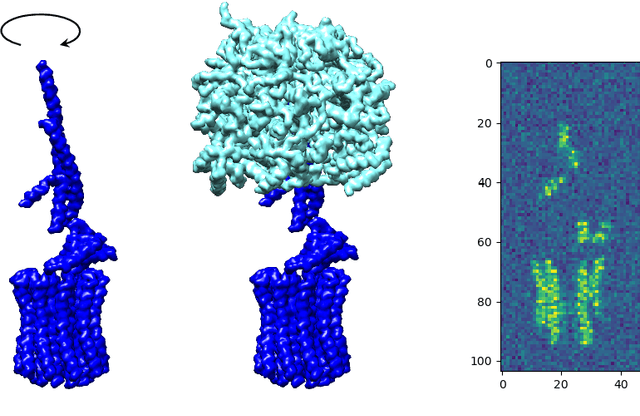
In this paper, we propose a novel approach for manifold learning that combines the Earthmover's distance (EMD) with the diffusion maps method for dimensionality reduction. We demonstrate the potential benefits of this approach for learning shape spaces of proteins and other flexible macromolecules using a simulated dataset of 3-D density maps that mimic the non-uniform rotary motion of ATP synthase. Our results show that EMD-based diffusion maps require far fewer samples to recover the intrinsic geometry than the standard diffusion maps algorithm that is based on the Euclidean distance. To reduce the computational burden of calculating the EMD for all volume pairs, we employ a wavelet-based approximation to the EMD which reduces the computation of the pairwise EMDs to a computation of pairwise weighted-$\ell_1$ distances between wavelet coefficient vectors.