Modeling Latent Neural Dynamics with Gaussian Process Switching Linear Dynamical Systems
Paper and Code
Jul 19, 2024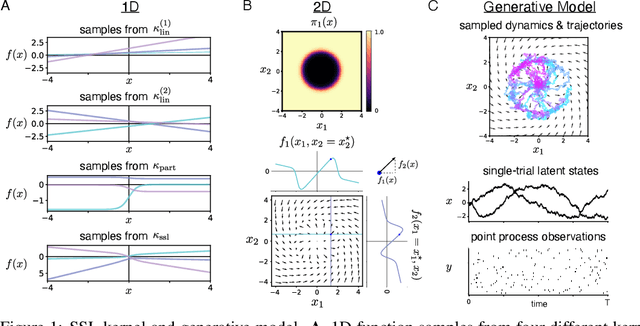
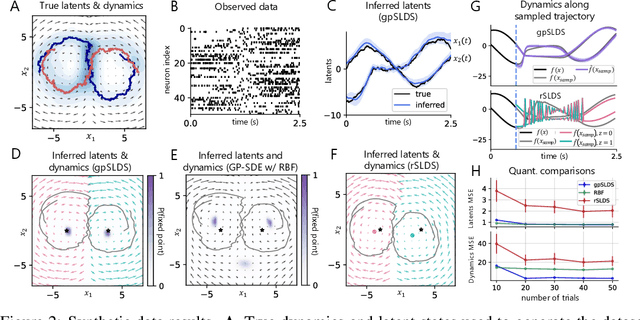
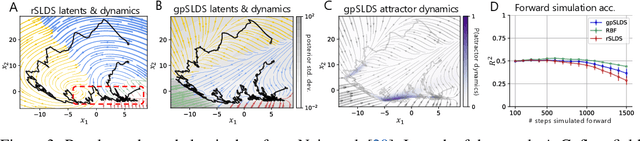
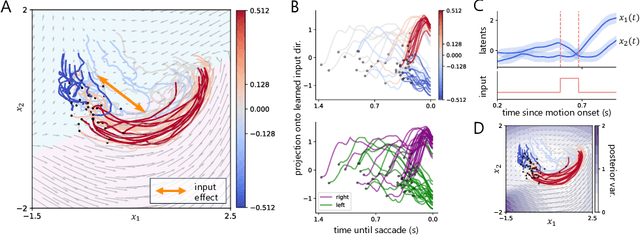
Understanding how the collective activity of neural populations relates to computation and ultimately behavior is a key goal in neuroscience. To this end, statistical methods which describe high-dimensional neural time series in terms of low-dimensional latent dynamics have played a fundamental role in characterizing neural systems. Yet, what constitutes a successful method involves two opposing criteria: (1) methods should be expressive enough to capture complex nonlinear dynamics, and (2) they should maintain a notion of interpretability often only warranted by simpler linear models. In this paper, we develop an approach that balances these two objectives: the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method builds on previous work modeling the latent state evolution via a stochastic differential equation whose nonlinear dynamics are described by a Gaussian process (GP-SDEs). We propose a novel kernel function which enforces smoothly interpolated locally linear dynamics, and therefore expresses flexible -- yet interpretable -- dynamics akin to those of recurrent switching linear dynamical systems (rSLDS). Our approach resolves key limitations of the rSLDS such as artifactual oscillations in dynamics near discrete state boundaries, while also providing posterior uncertainty estimates of the dynamics. To fit our models, we leverage a modified learning objective which improves the estimation accuracy of kernel hyperparameters compared to previous GP-SDE fitting approaches. We apply our method to synthetic data and data recorded in two neuroscience experiments and demonstrate favorable performance in comparison to the rSLDS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge