Machine Learning Prescriptive Canvas for Optimizing Business Outcomes

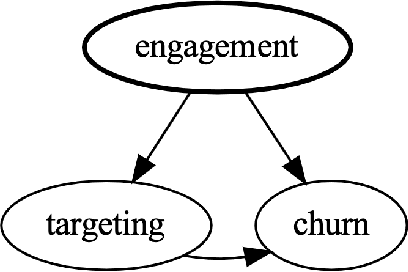
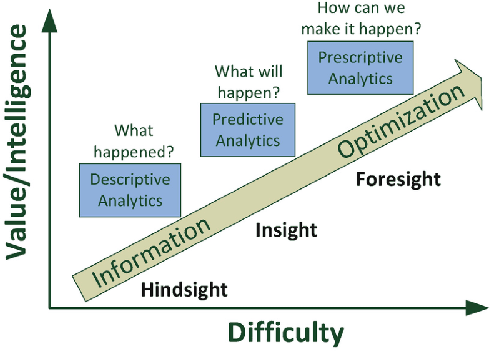
Data science has the potential to improve business in a variety of verticals. While the lion's share of data science projects uses a predictive approach, to drive improvements these predictions should become decisions. However, such a two-step approach is not only sub-optimal but might even degrade performance and fail the project. The alternative is to follow a prescriptive framing, where actions are "first citizens" so that the model produces a policy that prescribes an action to take, rather than predicting an outcome. In this paper, we explain why the prescriptive approach is important and provide a step-by-step methodology: the Prescriptive Canvas. The latter aims to improve framing and communication across the project stakeholders including project and data science managers towards a successful business impact.

Positivity Validation Detection and Explainability via Zero Fraction Multi-Hypothesis Testing and Asymmetrically Pruned Decision Trees

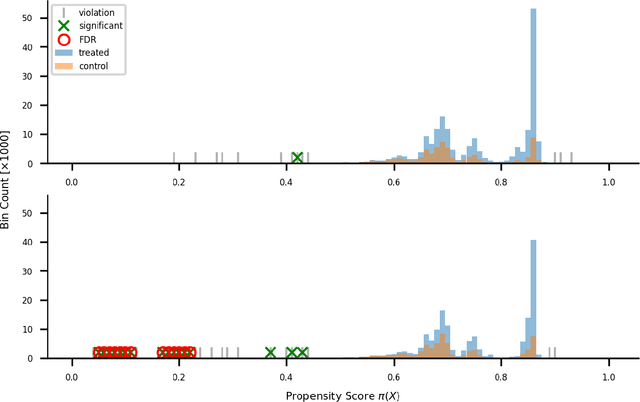
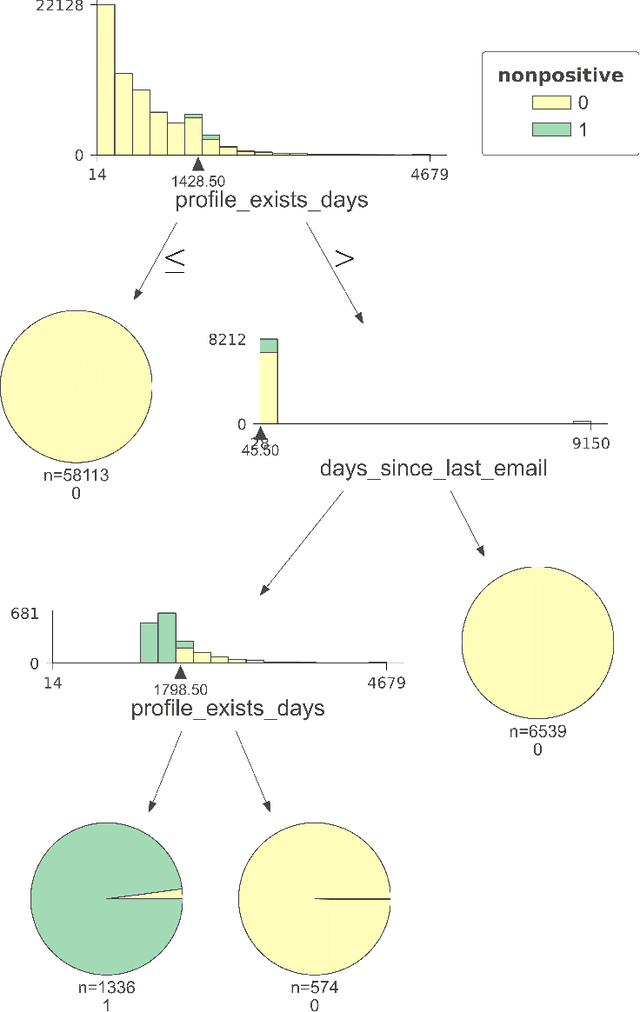
Positivity is one of the three conditions for causal inference from observational data. The standard way to validate positivity is to analyze the distribution of propensity. However, to democratize the ability to do causal inference by non-experts, it is required to design an algorithm to (i) test positivity and (ii) explain where in the covariate space positivity is lacking. The latter could be used to either suggest the limitation of further causal analysis and/or encourage experimentation where positivity is violated. The contribution of this paper is first present the problem of automatic positivity analysis and secondly to propose an algorithm based on a two steps process. The first step, models the propensity condition on the covariates and then analyze the latter distribution using multiple hypothesis testing to create positivity violation labels. The second step uses asymmetrically pruned decision trees for explainability. The latter is further converted into readable text a non-expert can understand. We demonstrate our method on a proprietary data-set of a large software enterprise.

DL-DDA -- Deep Learning based Dynamic Difficulty Adjustment with UX and Gameplay constraints

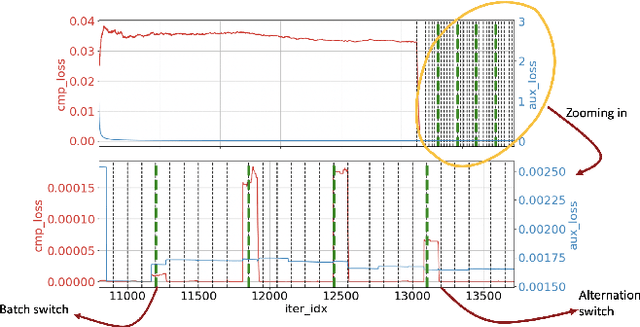
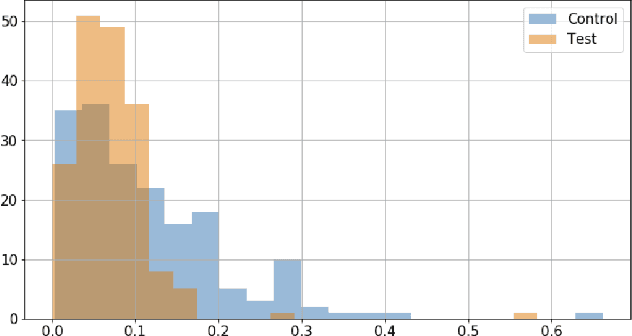
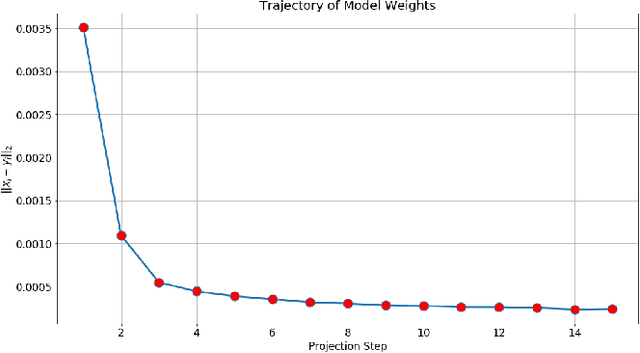
Dynamic difficulty adjustment ($DDA$) is a process of automatically changing a game difficulty for the optimization of user experience. It is a vital part of almost any modern game. Most existing DDA approaches concentrate on the experience of a player without looking at the rest of the players. We propose a method that automatically optimizes user experience while taking into consideration other players and macro constraints imposed by the game. The method is based on deep neural network architecture that involves a count loss constraint that has zero gradients in most of its support. We suggest a method to optimize this loss function and provide theoretical analysis for its performance. Finally, we provide empirical results of an internal experiment that was done on $200,000$ players and was found to outperform the corresponding manual heuristics crafted by game design experts.

Generalized Quantile Loss for Deep Neural Networks

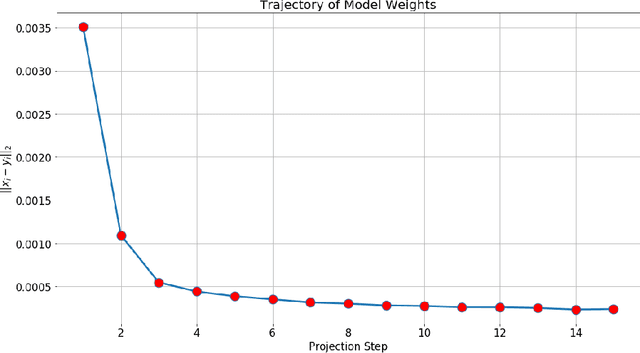
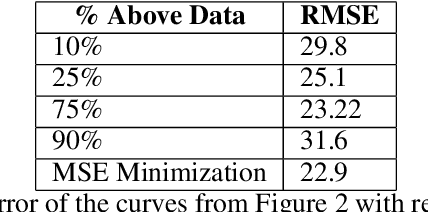
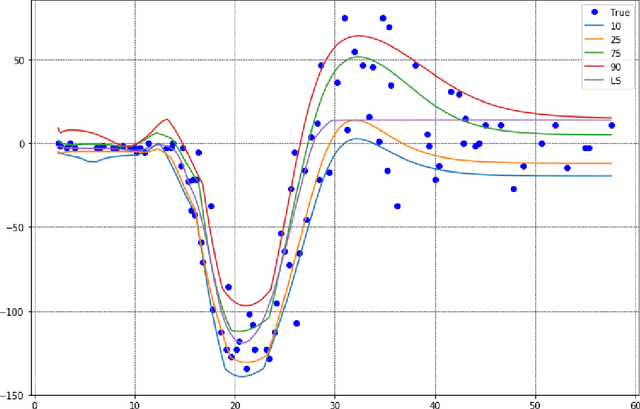
This note presents a simple way to add a count (or quantile) constraint to a regression neural net, such that given $n$ samples in the training set it guarantees that the prediction of $m<n$ samples will be larger than the actual value (the label). Unlike standard quantile regression networks, the presented method can be applied to any loss function and not necessarily to the standard quantile regression loss, which minimizes the mean absolute differences. Since this count constraint has zero gradients almost everywhere, it cannot be optimized using standard gradient descent methods. To overcome this problem, an alternation scheme, which is based on standard neural network optimization procedures, is presented with some theoretical analysis.

Majority Voting and the Condorcet's Jury Theorem

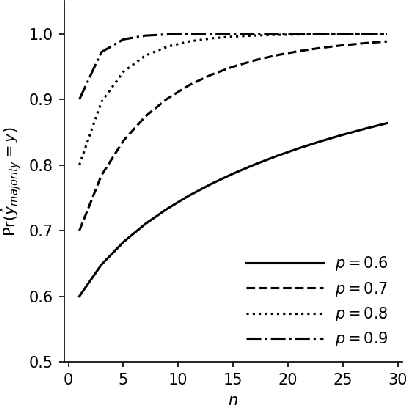
There is a striking relationship between a three hundred years old Political Science theorem named "Condorcet's jury theorem" (1785), which states that majorities are more likely to choose correctly when individual votes are often correct and independent, and a modern Machine Learning concept called "Strength of Weak Learnability" (1990), which describes a method for converting a weak learning algorithm into one that achieves arbitrarily high accuracy and stands in the basis of Ensemble Learning. Albeit the intuitive statement of Condorcet's theorem, we could not find a compact and simple rigorous mathematical proof of the theorem neither in classical handbooks of Machine Learning nor in published papers. By all means we do not claim to discover or reinvent a theory nor a result. We humbly want to offer a more publicly available simple derivation of the theorem. We will find joy in seeing more teachers of introduction-to-machine-learning courses use the proof we provide here as an exercise to explain the motivation of ensemble learning.

Fast and Accurate Gaussian Kernel Ridge Regression Using Matrix Decompositions for Preconditioning

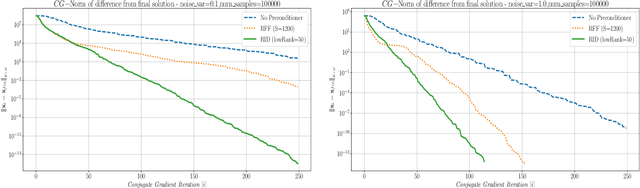
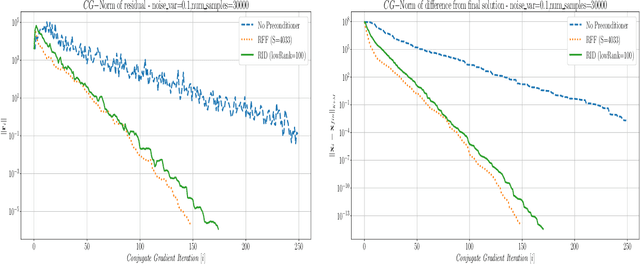
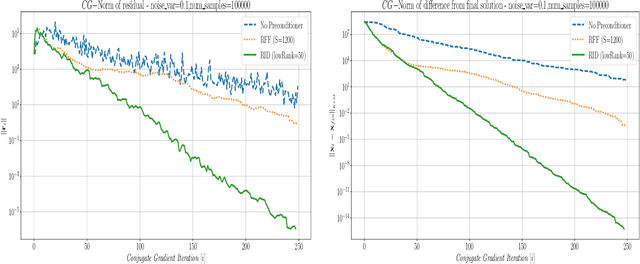
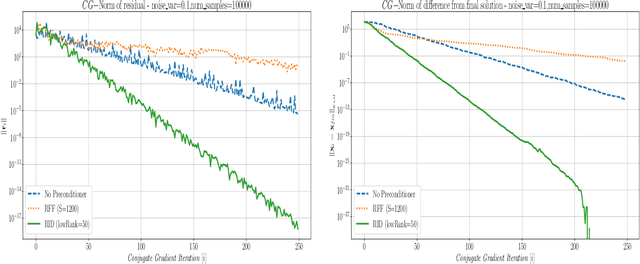
This paper presents a method for building a preconditioner for a kernel ridge regression problem, where the preconditioner is not only effective in its ability to reduce the condition number substantially, but also efficient in its application in terms of computational cost and memory consumption. The suggested approach is based on randomized matrix decomposition methods, combined with the fast multipole method to achieve an algorithm that can process large datasets in complexity linear to the number of data points. In addition, a detailed theoretical analysis is provided, including an upper bound to the condition number. Finally, for Gaussian kernels, the analysis shows that the required rank for a desired condition number can be determined directly from the dataset itself without performing any analysis on the kernel matrix.

Randomized LU decomposition: An Algorithm for Dictionaries Construction

In recent years, distinctive-dictionary construction has gained importance due to his usefulness in data processing. Usually, one or more dictionaries are constructed from a training data and then they are used to classify signals that did not participate in the training process. A new dictionary construction algorithm is introduced. It is based on a low-rank matrix factorization being achieved by the application of the randomized LU decomposition to a training data. This method is fast, scalable, parallelizable, consumes low memory, outperforms SVD in these categories and works also extremely well on large sparse matrices. In contrast to existing methods, the randomized LU decomposition constructs an under-complete dictionary, which simplifies both the construction and the classification processes of newly arrived signals. The dictionary construction is generic and general that fits different applications. We demonstrate the capabilities of this algorithm for file type identification, which is a fundamental task in digital security arena, performed nowadays for example by sandboxing mechanism, deep packet inspection, firewalls and anti-virus systems. We propose a content-based method that detects file types that neither depend on file extension nor on metadata. Such approach is harder to deceive and we show that only a few file fragments from a whole file are needed for a successful classification. Based on the constructed dictionaries, we show that the proposed method can effectively identify execution code fragments in PDF files. $\textbf{Keywords.}$ Dictionary construction, classification, LU decomposition, randomized LU decomposition, content-based file detection, computer security.

Similarity Search Over Graphs Using Localized Spectral Analysis

This paper provides a new similarity detection algorithm. Given an input set of multi-dimensional data points, where each data point is assumed to be multi-dimensional, and an additional reference data point for similarity finding, the algorithm uses kernel method that embeds the data points into a low dimensional manifold. Unlike other kernel methods, which consider the entire data for the embedding, our method selects a specific set of kernel eigenvectors. The eigenvectors are chosen to separate between the data points and the reference data point so that similar data points can be easily identified as being distinct from most of the members in the dataset.

Missing Entries Matrix Approximation and Completion

We describe several algorithms for matrix completion and matrix approximation when only some of its entries are known. The approximation constraint can be any whose approximated solution is known for the full matrix. For low rank approximations, similar algorithms appears recently in the literature under different names. In this work, we introduce new theorems for matrix approximation and show that these algorithms can be extended to handle different constraints such as nuclear norm, spectral norm, orthogonality constraints and more that are different than low rank approximations. As the algorithms can be viewed from an optimization point of view, we discuss their convergence to global solution for the convex case. We also discuss the optimal step size and show that it is fixed in each iteration. In addition, the derived matrix completion flow is robust and does not require any parameters. This matrix completion flow is applicable to different spectral minimizations and can be applied to physics, mathematics and electrical engineering problems such as data reconstruction of images and data coming from PDEs such as Helmholtz equation used for electromagnetic waves.

Potentials and Limits of Super-Resolution Algorithms and Signal Reconstruction from Sparse Data

A common distortion in videos is image instability in the form of chaotic (global and local displacements). Those instabilities can be used to enhance image resolution by using subpixel elastic registration. In this work, we investigate the performance of such methods over the ability to improve the resolution by accumulating several frames. The second part of this work deals with reconstruction of discrete signals from a subset of samples under different basis functions such as DFT, Haar, Walsh, Daubechies wavelets and CT (Radon) projections.