Randomized LU decomposition: An Algorithm for Dictionaries Construction

In recent years, distinctive-dictionary construction has gained importance due to his usefulness in data processing. Usually, one or more dictionaries are constructed from a training data and then they are used to classify signals that did not participate in the training process. A new dictionary construction algorithm is introduced. It is based on a low-rank matrix factorization being achieved by the application of the randomized LU decomposition to a training data. This method is fast, scalable, parallelizable, consumes low memory, outperforms SVD in these categories and works also extremely well on large sparse matrices. In contrast to existing methods, the randomized LU decomposition constructs an under-complete dictionary, which simplifies both the construction and the classification processes of newly arrived signals. The dictionary construction is generic and general that fits different applications. We demonstrate the capabilities of this algorithm for file type identification, which is a fundamental task in digital security arena, performed nowadays for example by sandboxing mechanism, deep packet inspection, firewalls and anti-virus systems. We propose a content-based method that detects file types that neither depend on file extension nor on metadata. Such approach is harder to deceive and we show that only a few file fragments from a whole file are needed for a successful classification. Based on the constructed dictionaries, we show that the proposed method can effectively identify execution code fragments in PDF files. $\textbf{Keywords.}$ Dictionary construction, classification, LU decomposition, randomized LU decomposition, content-based file detection, computer security.

Missing Entries Matrix Approximation and Completion

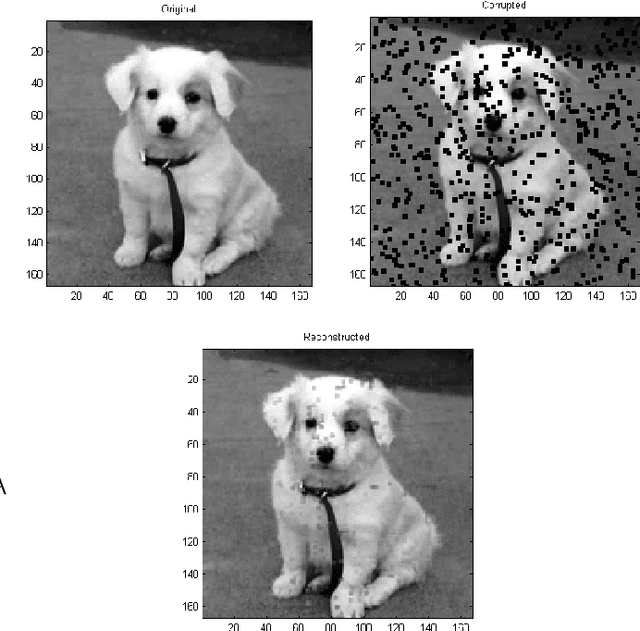
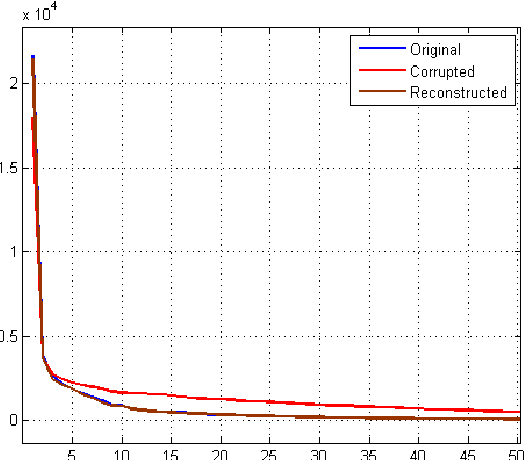
We describe several algorithms for matrix completion and matrix approximation when only some of its entries are known. The approximation constraint can be any whose approximated solution is known for the full matrix. For low rank approximations, similar algorithms appears recently in the literature under different names. In this work, we introduce new theorems for matrix approximation and show that these algorithms can be extended to handle different constraints such as nuclear norm, spectral norm, orthogonality constraints and more that are different than low rank approximations. As the algorithms can be viewed from an optimization point of view, we discuss their convergence to global solution for the convex case. We also discuss the optimal step size and show that it is fixed in each iteration. In addition, the derived matrix completion flow is robust and does not require any parameters. This matrix completion flow is applicable to different spectral minimizations and can be applied to physics, mathematics and electrical engineering problems such as data reconstruction of images and data coming from PDEs such as Helmholtz equation used for electromagnetic waves.