Randomized LU decomposition: An Algorithm for Dictionaries Construction

In recent years, distinctive-dictionary construction has gained importance due to his usefulness in data processing. Usually, one or more dictionaries are constructed from a training data and then they are used to classify signals that did not participate in the training process. A new dictionary construction algorithm is introduced. It is based on a low-rank matrix factorization being achieved by the application of the randomized LU decomposition to a training data. This method is fast, scalable, parallelizable, consumes low memory, outperforms SVD in these categories and works also extremely well on large sparse matrices. In contrast to existing methods, the randomized LU decomposition constructs an under-complete dictionary, which simplifies both the construction and the classification processes of newly arrived signals. The dictionary construction is generic and general that fits different applications. We demonstrate the capabilities of this algorithm for file type identification, which is a fundamental task in digital security arena, performed nowadays for example by sandboxing mechanism, deep packet inspection, firewalls and anti-virus systems. We propose a content-based method that detects file types that neither depend on file extension nor on metadata. Such approach is harder to deceive and we show that only a few file fragments from a whole file are needed for a successful classification. Based on the constructed dictionaries, we show that the proposed method can effectively identify execution code fragments in PDF files. $\textbf{Keywords.}$ Dictionary construction, classification, LU decomposition, randomized LU decomposition, content-based file detection, computer security.

Incomplete Pivoted QR-based Dimensionality Reduction

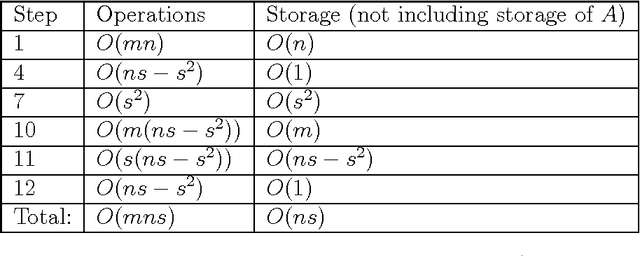
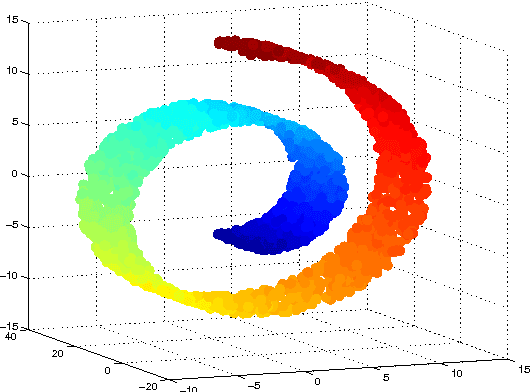
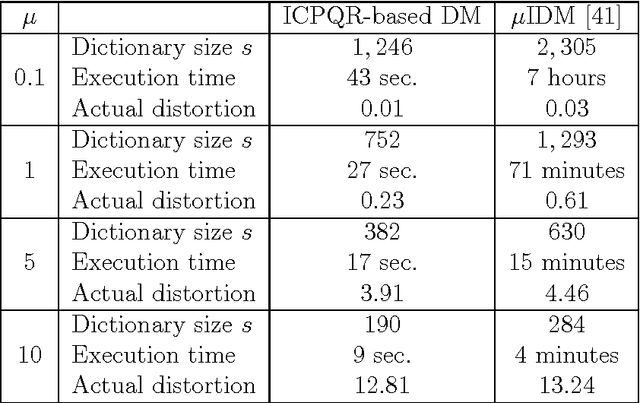
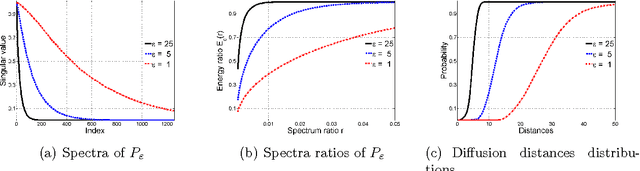
High-dimensional big data appears in many research fields such as image recognition, biology and collaborative filtering. Often, the exploration of such data by classic algorithms is encountered with difficulties due to `curse of dimensionality' phenomenon. Therefore, dimensionality reduction methods are applied to the data prior to its analysis. Many of these methods are based on principal components analysis, which is statistically driven, namely they map the data into a low-dimension subspace that preserves significant statistical properties of the high-dimensional data. As a consequence, such methods do not directly address the geometry of the data, reflected by the mutual distances between multidimensional data point. Thus, operations such as classification, anomaly detection or other machine learning tasks may be affected. This work provides a dictionary-based framework for geometrically driven data analysis that includes dimensionality reduction, out-of-sample extension and anomaly detection. It embeds high-dimensional data in a low-dimensional subspace. This embedding preserves the original high-dimensional geometry of the data up to a user-defined distortion rate. In addition, it identifies a subset of landmark data points that constitute a dictionary for the analyzed dataset. The dictionary enables to have a natural extension of the low-dimensional embedding to out-of-sample data points, which gives rise to a distortion-based criterion for anomaly detection. The suggested method is demonstrated on synthetic and real-world datasets and achieves good results for classification, anomaly detection and out-of-sample tasks.