SEL-CIE: Knowledge-Guided Self-Supervised Learning Framework for CIE-XYZ Reconstruction from Non-Linear sRGB Images

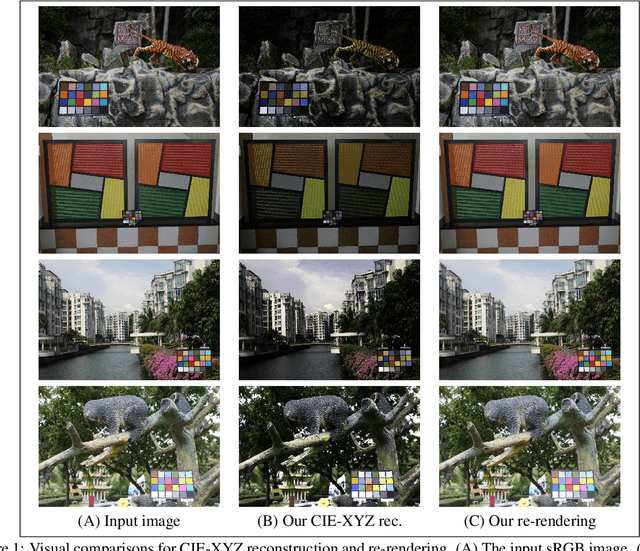
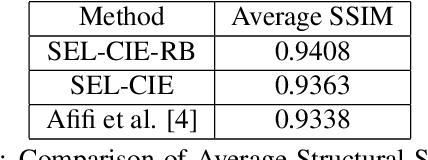
Modern cameras typically offer two types of image states: a minimally processed linear raw RGB image representing the raw sensor data, and a highly-processed non-linear image state, such as the sRGB state. The CIE-XYZ color space is a device-independent linear space used as part of the camera pipeline and can be helpful for computer vision tasks, such as image deblurring, dehazing, and color recognition tasks in medical applications, where color accuracy is important. However, images are usually saved in non-linear states, and achieving CIE-XYZ color images using conventional methods is not always possible. To tackle this issue, classical methodologies have been developed that focus on reversing the acquisition pipeline. More recently, supervised learning has been employed, using paired CIE-XYZ and sRGB representations of identical images. However, obtaining a large-scale dataset of CIE-XYZ and sRGB pairs can be challenging. To overcome this limitation and mitigate the reliance on large amounts of paired data, self-supervised learning (SSL) can be utilized as a substitute for relying solely on paired data. This paper proposes a framework for using SSL methods alongside paired data to reconstruct CIE-XYZ images and re-render sRGB images, outperforming existing approaches. The proposed framework is applied to the sRGB2XYZ dataset.

TabADM: Unsupervised Tabular Anomaly Detection with Diffusion Models

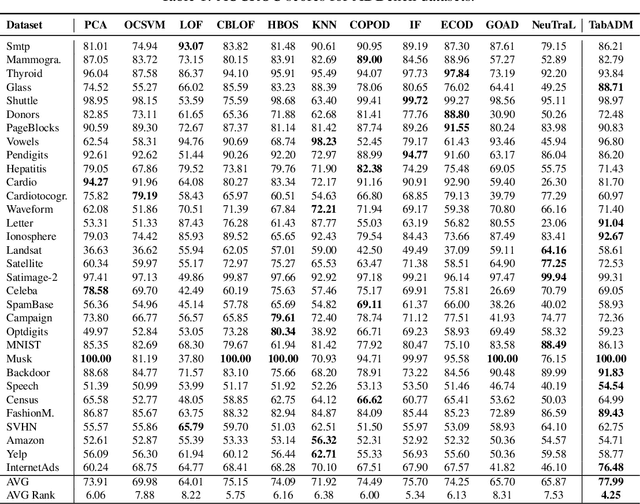
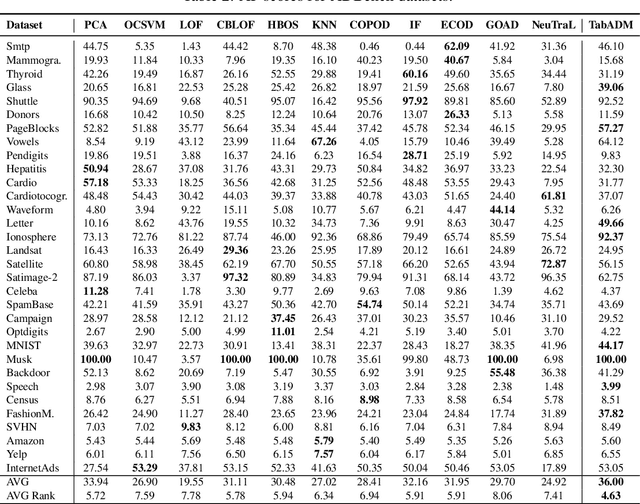
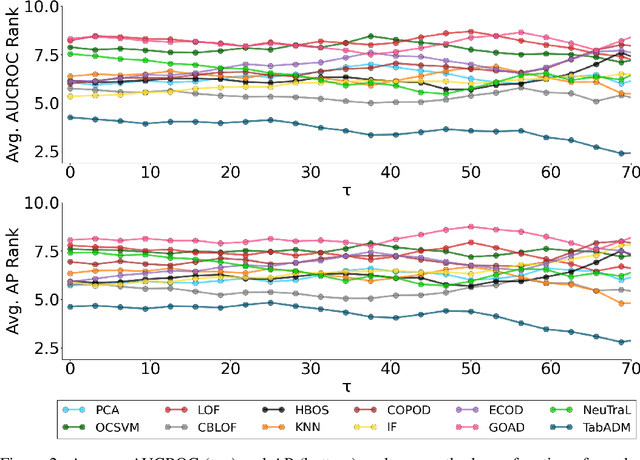
Tables are an abundant form of data with use cases across all scientific fields. Real-world datasets often contain anomalous samples that can negatively affect downstream analysis. In this work, we only assume access to contaminated data and present a diffusion-based probabilistic model effective for unsupervised anomaly detection. Our model is trained to learn the density of normal samples by utilizing a unique rejection scheme to attenuate the influence of anomalies on the density estimation. At inference, we identify anomalies as samples in low-density regions. We use real data to demonstrate that our method improves detection capabilities over baselines. Furthermore, our method is relatively stable to the dimension of the data and does not require extensive hyperparameter tuning.

Cross-boosting of WNNM Image Denoising method by Directional Wavelet Packets

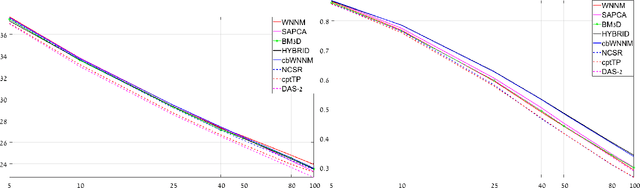
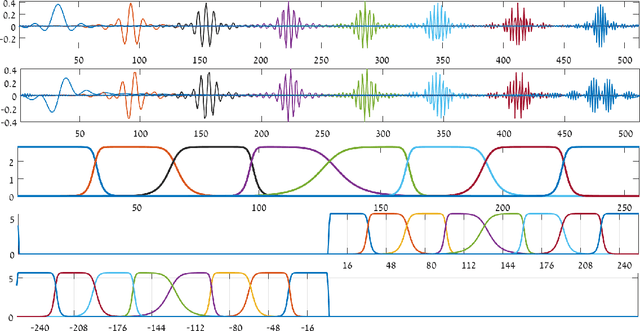
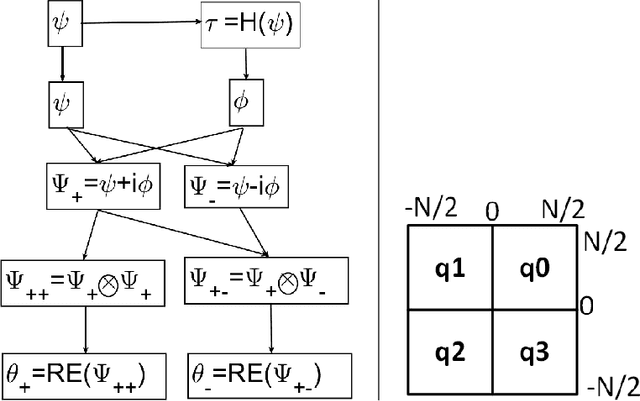
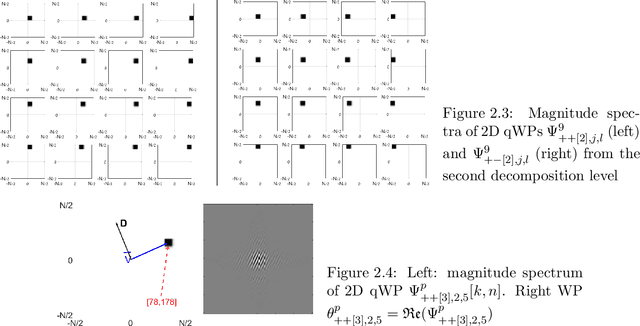
The paper presents an image denoising scheme by combining a method that is based on directional quasi-analytic wavelet packets (qWPs) with the state-of-the-art Weighted Nuclear Norm Minimization (WNNM) denoising algorithm. The qWP-based denoising method (qWPdn) consists of multiscale qWP transform of the degraded image, application of adaptive localized soft thresholding to the transform coefficients using the Bivariate Shrinkage methodology, and restoration of the image from the thresholded coefficients from several decomposition levels. The combined method consists of several iterations of qWPdn and WNNM algorithms in a way that at each iteration the output from one algorithm boosts the input to the other. The proposed methodology couples the qWPdn capabilities to capture edges and fine texture patterns even in the severely corrupted images with utilizing the non-local self-similarity in real images that is inherent in the WNNM algorithm. Multiple experiments, which compared the proposed methodology with six advanced denoising algorithms, including WNNM, confirmed that the combined cross-boosting algorithm outperforms most of them in terms of both quantitative measure and visual perception quality.

Imbalanced Classification via a Tabular Translation GAN

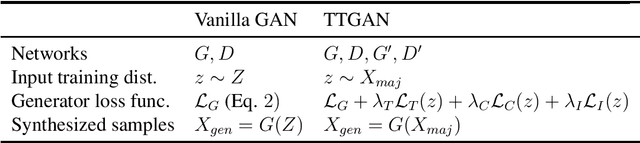
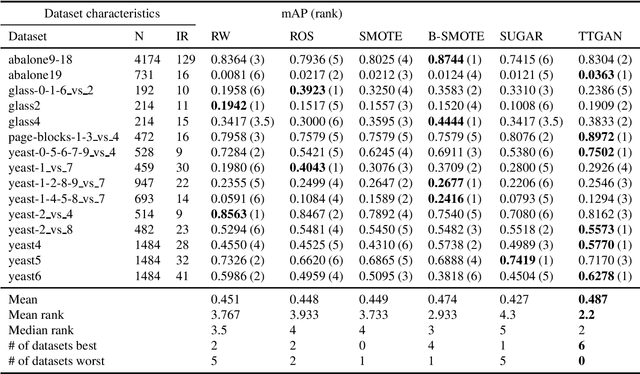
When presented with a binary classification problem where the data exhibits severe class imbalance, most standard predictive methods may fail to accurately model the minority class. We present a model based on Generative Adversarial Networks which uses additional regularization losses to map majority samples to corresponding synthetic minority samples. This translation mechanism encourages the synthesized samples to be close to the class boundary. Furthermore, we explore a selection criterion to retain the most useful of the synthesized samples. Experimental results using several downstream classifiers on a variety of tabular class-imbalanced datasets show that the proposed method improves average precision when compared to alternative re-weighting and oversampling techniques.

Search and Score-Based Waterfall Auction Optimization

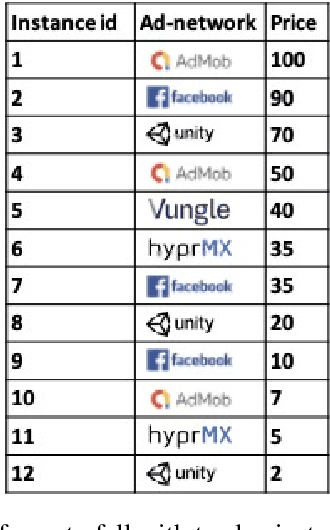
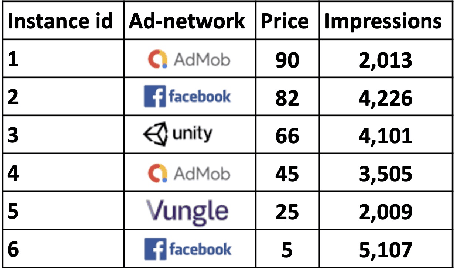
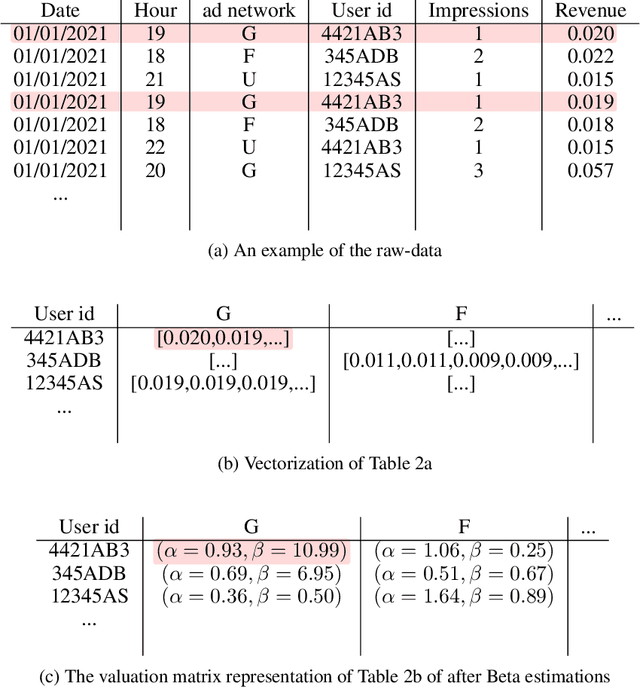
Online advertising is a major source of income for many online companies. One common approach is to sell online advertisements via waterfall auctions, where a publisher makes sequential price offers to ad networks. The publisher controls the order and prices of the waterfall and by that aims to maximize his revenue. In this work, we propose a methodology to learn a waterfall strategy from historical data by wisely searching in the space of possible waterfalls and selecting the one leading to the highest revenue. The contribution of this work is twofold; First, we propose a novel method to estimate the valuation distribution of each user with respect to each ad network. Second, we utilize the valuation matrix to score our candidate waterfalls as part of a procedure that iteratively searches in local neighborhoods. Our framework guarantees that the waterfall revenue improves between iterations until converging to a local optimum. Real-world demonstrations are provided to show that the proposed method improves the total revenue of real-world waterfalls compared to manual expert optimization. Finally, the code and the data are available here.

Deep Gated Canonical Correlation Analysis

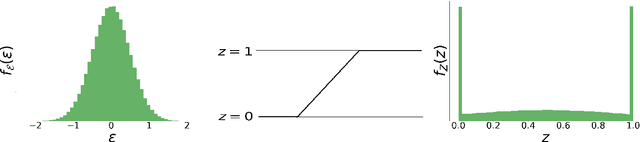
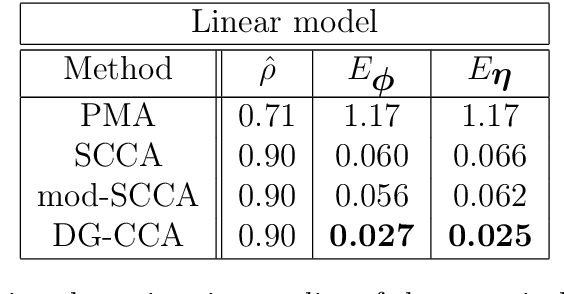
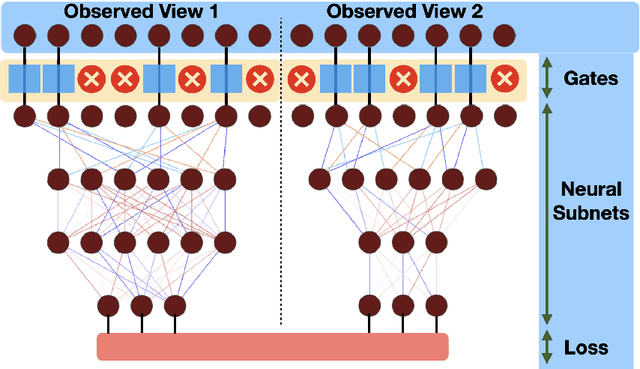
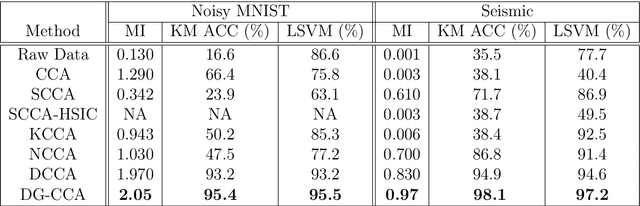
Canonical Correlation Analysis (CCA) models can extract informative correlated representations from multimodal unlabelled data. Despite their success, CCA models may break if the number of variables exceeds the number of samples. We propose Deep Gated-CCA, a method for learning correlated representations based on a sparse subset of variables from two observed modalities. The proposed procedure learns two non-linear transformations and simultaneously gates the input variables to identify a subset of most correlated variables. The non-linear transformations are learned by training two neural networks to maximize a shared correlation loss defined based on their outputs. Gating is obtained by adding an approximate $\ell_0$ regularization term applied to the input variables. This approximation relies on a recently proposed continuous Gaussian based relaxation for Bernoulli variables which act as gates. We demonstrate the efficacy of the method using several synthetic and real examples. Most notably, the method outperforms other linear and non-linear CCA models.

Majority Voting and the Condorcet's Jury Theorem

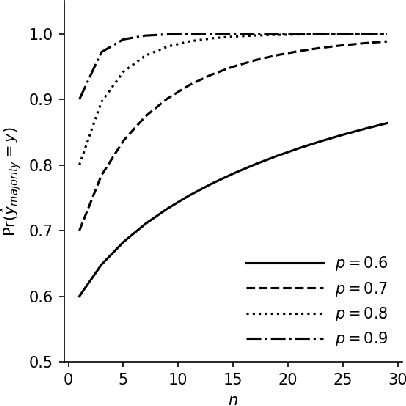
There is a striking relationship between a three hundred years old Political Science theorem named "Condorcet's jury theorem" (1785), which states that majorities are more likely to choose correctly when individual votes are often correct and independent, and a modern Machine Learning concept called "Strength of Weak Learnability" (1990), which describes a method for converting a weak learning algorithm into one that achieves arbitrarily high accuracy and stands in the basis of Ensemble Learning. Albeit the intuitive statement of Condorcet's theorem, we could not find a compact and simple rigorous mathematical proof of the theorem neither in classical handbooks of Machine Learning nor in published papers. By all means we do not claim to discover or reinvent a theory nor a result. We humbly want to offer a more publicly available simple derivation of the theorem. We will find joy in seeing more teachers of introduction-to-machine-learning courses use the proof we provide here as an exercise to explain the motivation of ensemble learning.

Kernel Scaling for Manifold Learning and Classification

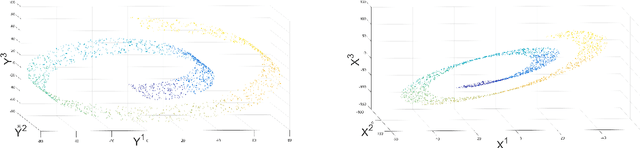
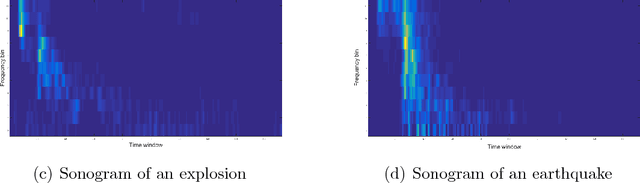
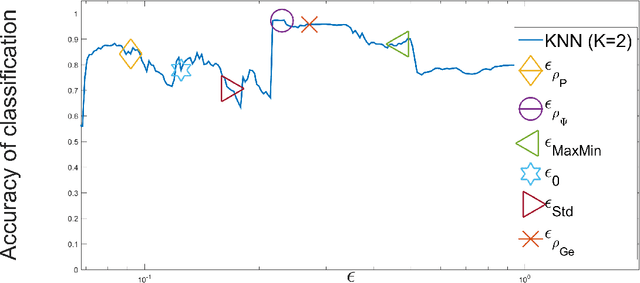
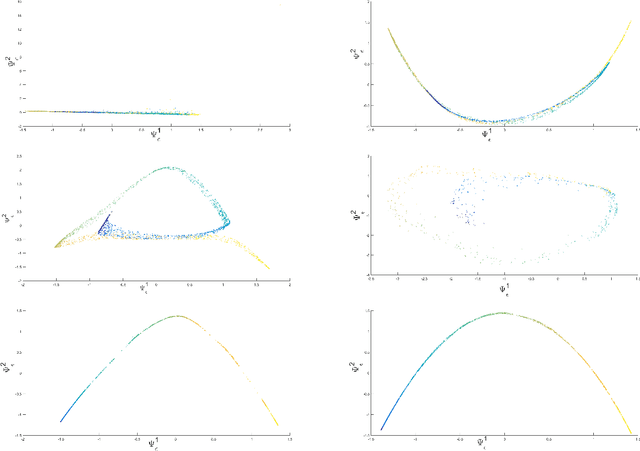
Kernel methods play a critical role in many dimensionality reduction algorithms. They are useful in manifold learning, classification, clustering and other machine learning tasks. Setting the kernel's scale parameter, also referred as the kernel's bandwidth, highly affects the extracted low-dimensional representation. We propose to set a scale parameter that is tailored to the desired application such as classification and manifold learning. The scale computation for the manifold learning task enables that the dimension of the extracted embedding equals the intrinsic dimension estimation. Three methods are proposed for scale computation in a classification task. The proposed frameworks are simulated on artificial and real datasets. The results show a high correlation between optimal classification rates and the computed scaling.

MultiView Diffusion Maps

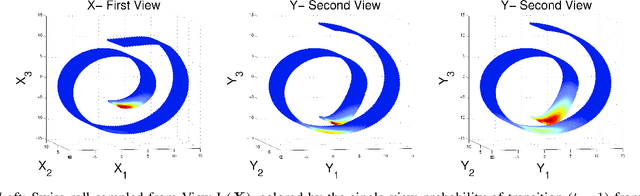
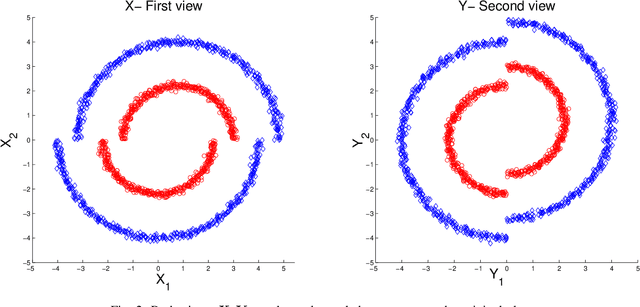
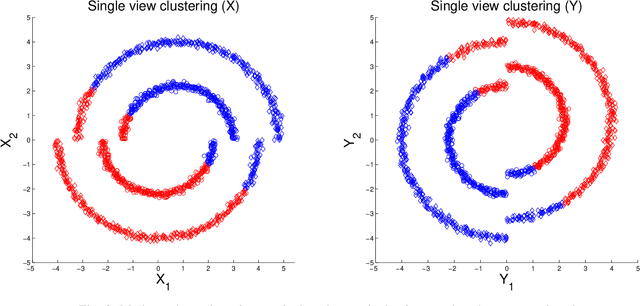
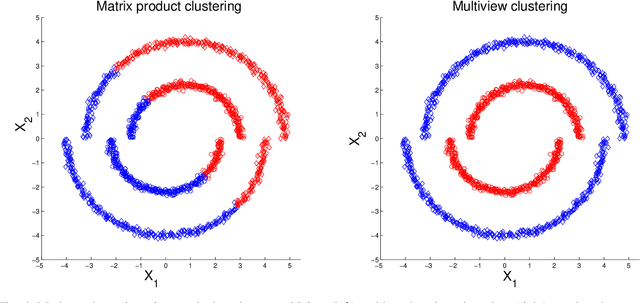
In this study we consider learning a reduced dimensionality representation from datasets obtained under multiple views. Such multiple views of datasets can be obtained, for example, when the same underlying process is observed using several different modalities, or measured with different instrumentation. Our goal is to effectively exploit the availability of such multiple views for various purposes, such as non-linear embedding, manifold learning, spectral clustering, anomaly detection and non-linear system identification. Our proposed method exploits the intrinsic relation within each view, as well as the mutual relations between views. We do this by defining a cross-view model, in which an implied Random Walk process between objects is restrained to hop between the different views. Our method is robust to scaling of each dataset, and is insensitive to small structural changes in the data. Within this framework, we define new diffusion distances and analyze the spectra of the implied kernels. We demonstrate the applicability of the proposed approach on both artificial and real data sets.

Incomplete Pivoted QR-based Dimensionality Reduction

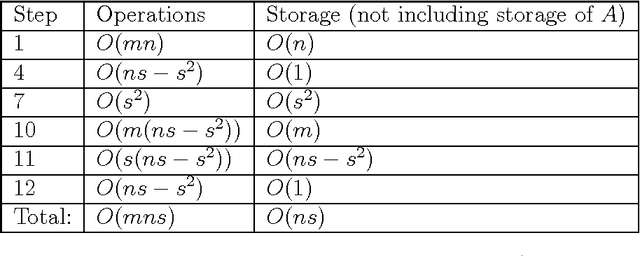
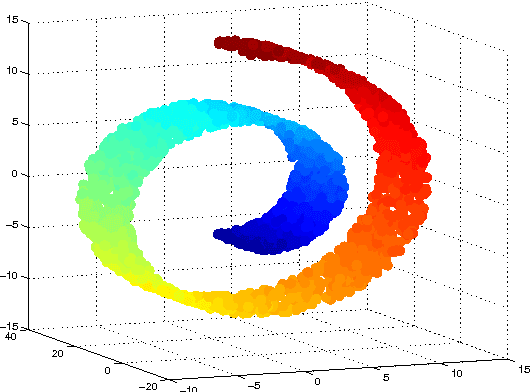
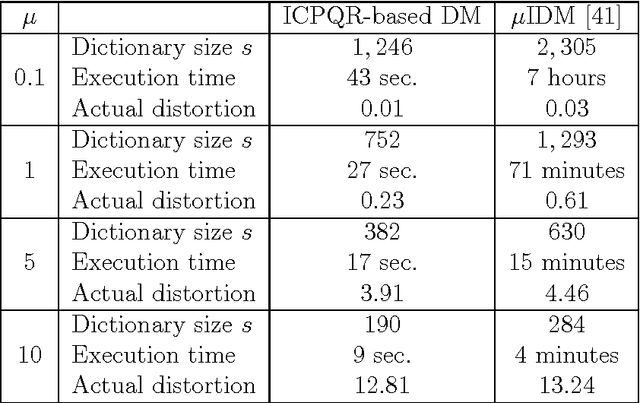
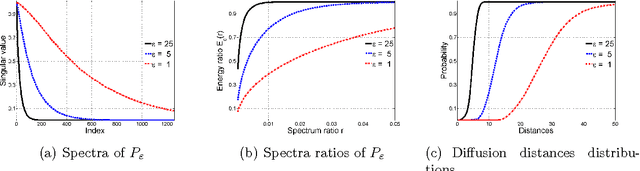
High-dimensional big data appears in many research fields such as image recognition, biology and collaborative filtering. Often, the exploration of such data by classic algorithms is encountered with difficulties due to `curse of dimensionality' phenomenon. Therefore, dimensionality reduction methods are applied to the data prior to its analysis. Many of these methods are based on principal components analysis, which is statistically driven, namely they map the data into a low-dimension subspace that preserves significant statistical properties of the high-dimensional data. As a consequence, such methods do not directly address the geometry of the data, reflected by the mutual distances between multidimensional data point. Thus, operations such as classification, anomaly detection or other machine learning tasks may be affected. This work provides a dictionary-based framework for geometrically driven data analysis that includes dimensionality reduction, out-of-sample extension and anomaly detection. It embeds high-dimensional data in a low-dimensional subspace. This embedding preserves the original high-dimensional geometry of the data up to a user-defined distortion rate. In addition, it identifies a subset of landmark data points that constitute a dictionary for the analyzed dataset. The dictionary enables to have a natural extension of the low-dimensional embedding to out-of-sample data points, which gives rise to a distortion-based criterion for anomaly detection. The suggested method is demonstrated on synthetic and real-world datasets and achieves good results for classification, anomaly detection and out-of-sample tasks.