A Causal Approach for Business Optimization: Application on an Online Marketplace

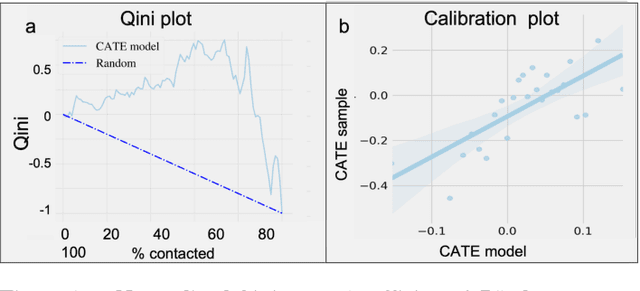
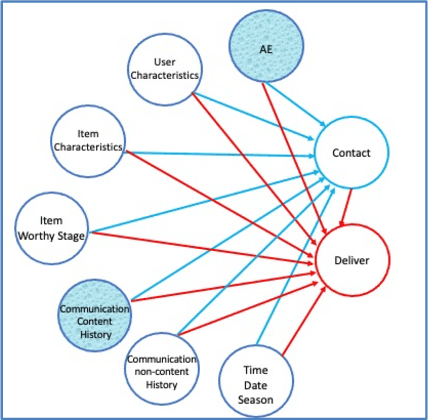
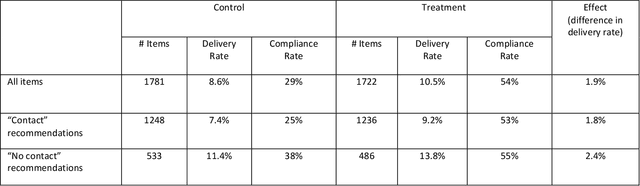
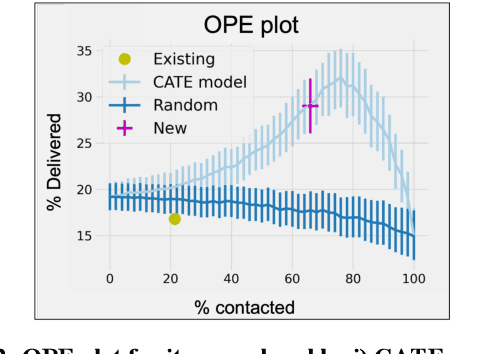
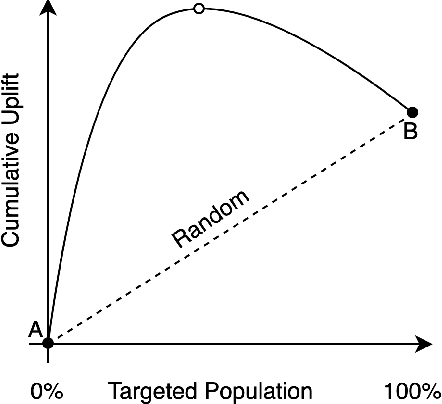
A common sales strategy involves having account executives (AEs) actively reach out and contact potential customers. However, not all contact attempts have a positive effect: some attempts do not change customer decisions, while others might even interfere with the desired outcome. In this work we propose using causal inference to estimate the effect of contacting each potential customer and setting the contact policy accordingly. We demonstrate this approach on data from Worthy, an online jewelry marketplace. We examined the Worthy business process to identify relevant decisions and outcomes, and formalized assumptions on how they were made. Using causal tools, we selected a decision point where improving AE contact activity appeared to be promising. We then generated a personalized policy and recommended reaching out only to customers for whom it would be beneficial. Finally, we validated the results in an A\B test over a 3-month period, resulting in an increase in item delivery rate of the targeted population by 22% (p-value=0.026). This policy is now being used on an ongoing basis.

Machine Learning Prescriptive Canvas for Optimizing Business Outcomes

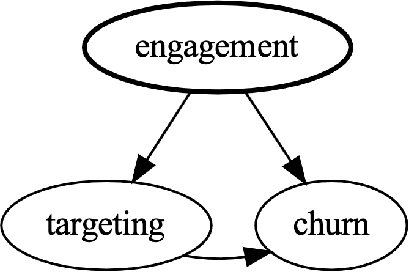
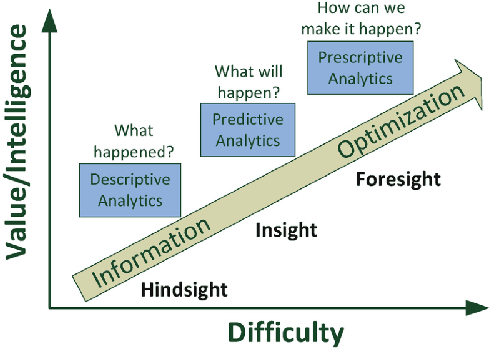
Data science has the potential to improve business in a variety of verticals. While the lion's share of data science projects uses a predictive approach, to drive improvements these predictions should become decisions. However, such a two-step approach is not only sub-optimal but might even degrade performance and fail the project. The alternative is to follow a prescriptive framing, where actions are "first citizens" so that the model produces a policy that prescribes an action to take, rather than predicting an outcome. In this paper, we explain why the prescriptive approach is important and provide a step-by-step methodology: the Prescriptive Canvas. The latter aims to improve framing and communication across the project stakeholders including project and data science managers towards a successful business impact.

Positivity Validation Detection and Explainability via Zero Fraction Multi-Hypothesis Testing and Asymmetrically Pruned Decision Trees

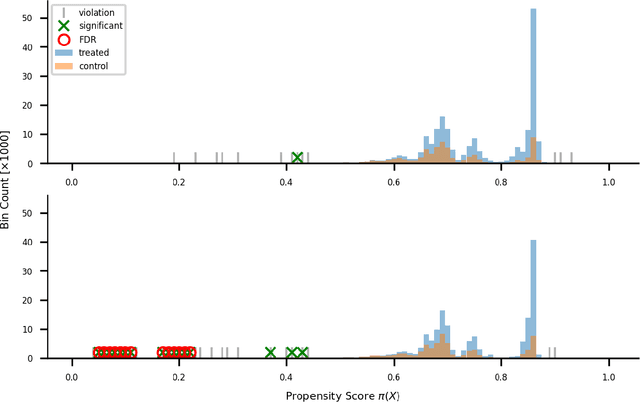
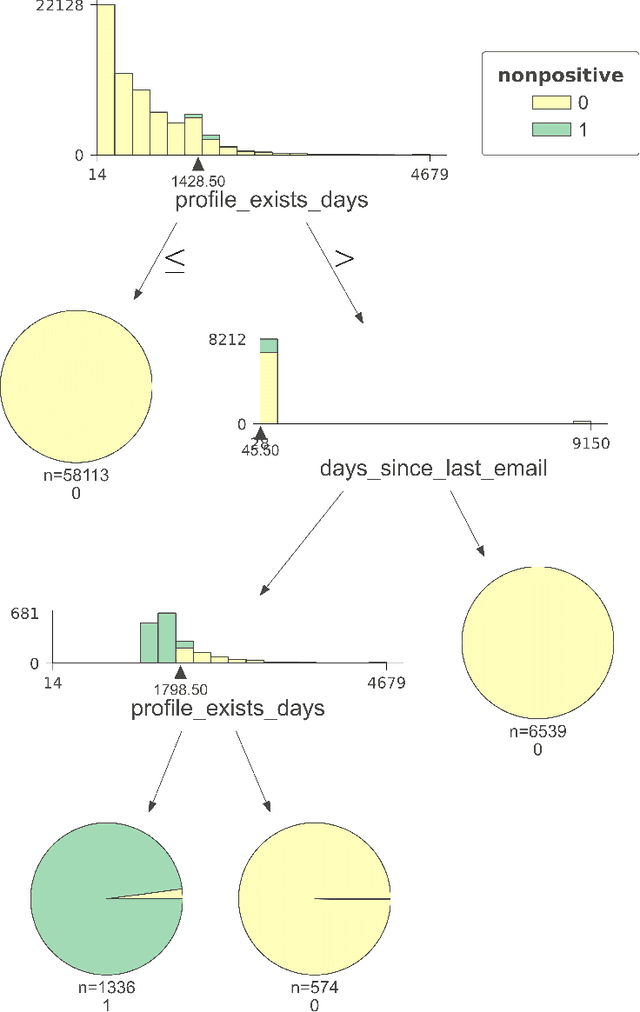
Positivity is one of the three conditions for causal inference from observational data. The standard way to validate positivity is to analyze the distribution of propensity. However, to democratize the ability to do causal inference by non-experts, it is required to design an algorithm to (i) test positivity and (ii) explain where in the covariate space positivity is lacking. The latter could be used to either suggest the limitation of further causal analysis and/or encourage experimentation where positivity is violated. The contribution of this paper is first present the problem of automatic positivity analysis and secondly to propose an algorithm based on a two steps process. The first step, models the propensity condition on the covariates and then analyze the latter distribution using multiple hypothesis testing to create positivity violation labels. The second step uses asymmetrically pruned decision trees for explainability. The latter is further converted into readable text a non-expert can understand. We demonstrate our method on a proprietary data-set of a large software enterprise.

Majority Voting and the Condorcet's Jury Theorem

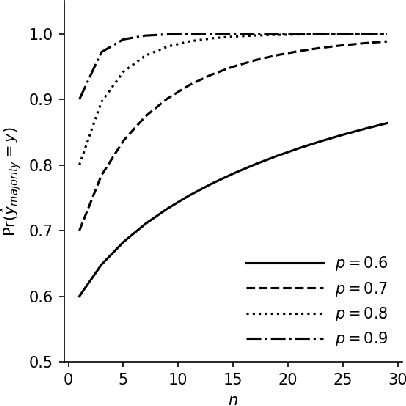
There is a striking relationship between a three hundred years old Political Science theorem named "Condorcet's jury theorem" (1785), which states that majorities are more likely to choose correctly when individual votes are often correct and independent, and a modern Machine Learning concept called "Strength of Weak Learnability" (1990), which describes a method for converting a weak learning algorithm into one that achieves arbitrarily high accuracy and stands in the basis of Ensemble Learning. Albeit the intuitive statement of Condorcet's theorem, we could not find a compact and simple rigorous mathematical proof of the theorem neither in classical handbooks of Machine Learning nor in published papers. By all means we do not claim to discover or reinvent a theory nor a result. We humbly want to offer a more publicly available simple derivation of the theorem. We will find joy in seeing more teachers of introduction-to-machine-learning courses use the proof we provide here as an exercise to explain the motivation of ensemble learning.