DL-DDA -- Deep Learning based Dynamic Difficulty Adjustment with UX and Gameplay constraints

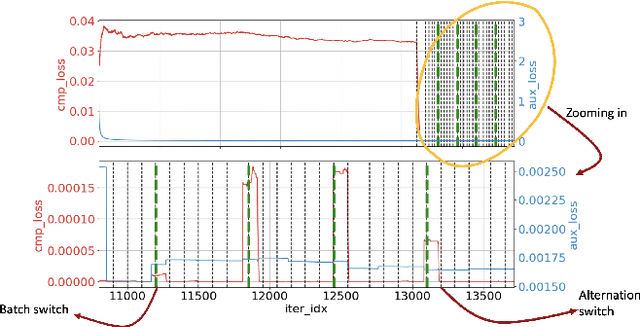
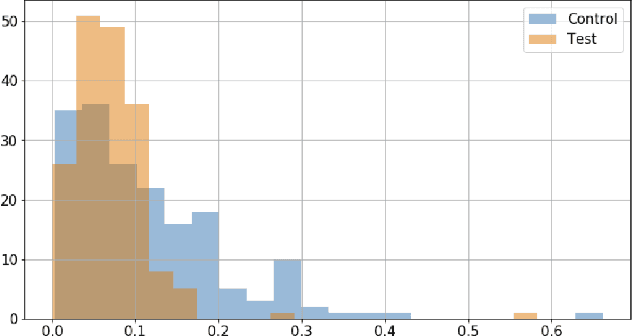
Dynamic difficulty adjustment ($DDA$) is a process of automatically changing a game difficulty for the optimization of user experience. It is a vital part of almost any modern game. Most existing DDA approaches concentrate on the experience of a player without looking at the rest of the players. We propose a method that automatically optimizes user experience while taking into consideration other players and macro constraints imposed by the game. The method is based on deep neural network architecture that involves a count loss constraint that has zero gradients in most of its support. We suggest a method to optimize this loss function and provide theoretical analysis for its performance. Finally, we provide empirical results of an internal experiment that was done on $200,000$ players and was found to outperform the corresponding manual heuristics crafted by game design experts.

Generalized Quantile Loss for Deep Neural Networks

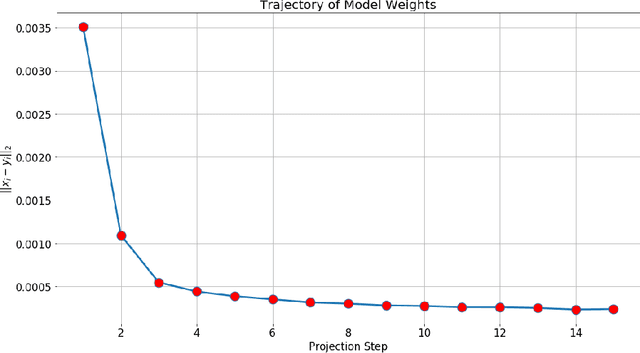
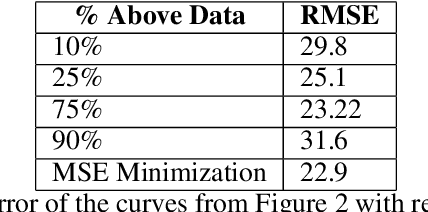
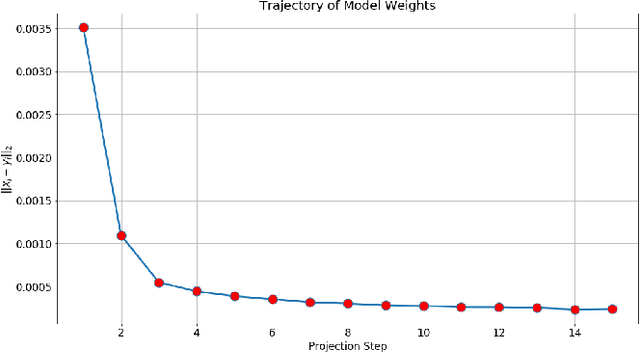
This note presents a simple way to add a count (or quantile) constraint to a regression neural net, such that given $n$ samples in the training set it guarantees that the prediction of $m<n$ samples will be larger than the actual value (the label). Unlike standard quantile regression networks, the presented method can be applied to any loss function and not necessarily to the standard quantile regression loss, which minimizes the mean absolute differences. Since this count constraint has zero gradients almost everywhere, it cannot be optimized using standard gradient descent methods. To overcome this problem, an alternation scheme, which is based on standard neural network optimization procedures, is presented with some theoretical analysis.

Majority Voting and the Condorcet's Jury Theorem

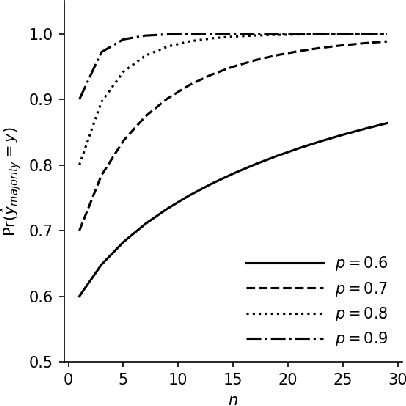
There is a striking relationship between a three hundred years old Political Science theorem named "Condorcet's jury theorem" (1785), which states that majorities are more likely to choose correctly when individual votes are often correct and independent, and a modern Machine Learning concept called "Strength of Weak Learnability" (1990), which describes a method for converting a weak learning algorithm into one that achieves arbitrarily high accuracy and stands in the basis of Ensemble Learning. Albeit the intuitive statement of Condorcet's theorem, we could not find a compact and simple rigorous mathematical proof of the theorem neither in classical handbooks of Machine Learning nor in published papers. By all means we do not claim to discover or reinvent a theory nor a result. We humbly want to offer a more publicly available simple derivation of the theorem. We will find joy in seeing more teachers of introduction-to-machine-learning courses use the proof we provide here as an exercise to explain the motivation of ensemble learning.