Generalized Quantile Loss for Deep Neural Networks
Paper and Code
Dec 28, 2020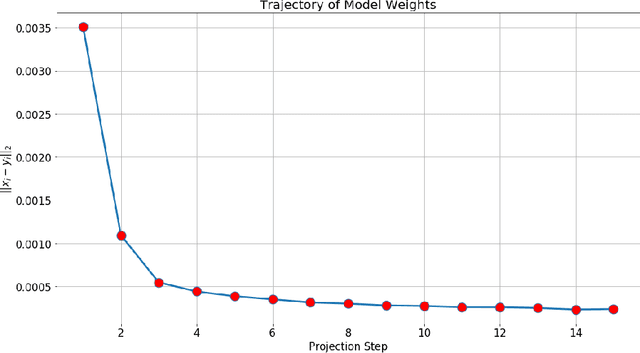
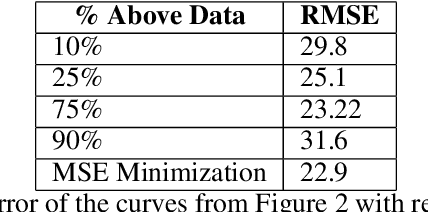
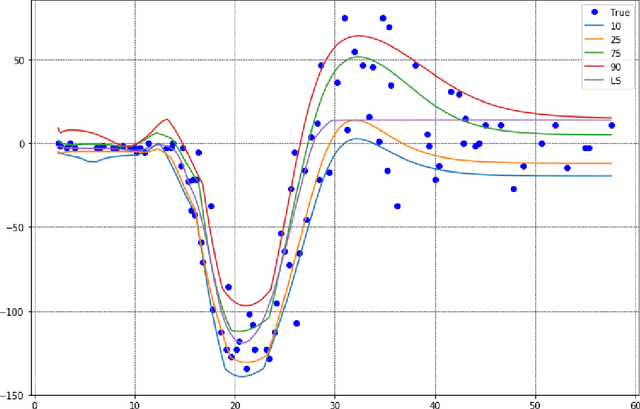
This note presents a simple way to add a count (or quantile) constraint to a regression neural net, such that given $n$ samples in the training set it guarantees that the prediction of $m<n$ samples will be larger than the actual value (the label). Unlike standard quantile regression networks, the presented method can be applied to any loss function and not necessarily to the standard quantile regression loss, which minimizes the mean absolute differences. Since this count constraint has zero gradients almost everywhere, it cannot be optimized using standard gradient descent methods. To overcome this problem, an alternation scheme, which is based on standard neural network optimization procedures, is presented with some theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge