Arie Yeredor
A Unified MDL-based Binning and Tensor Factorization Framework for PDF Estimation
Apr 25, 2025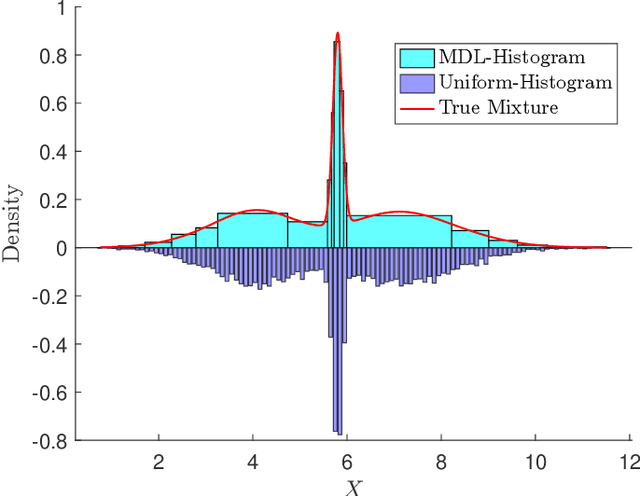
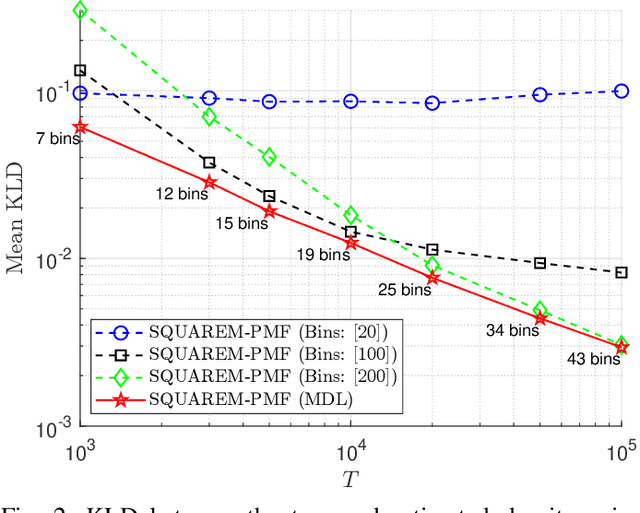
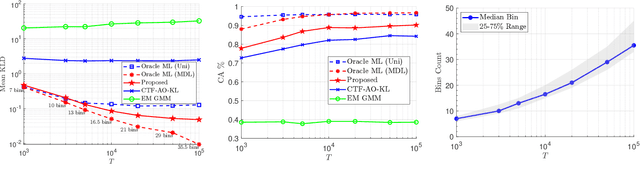
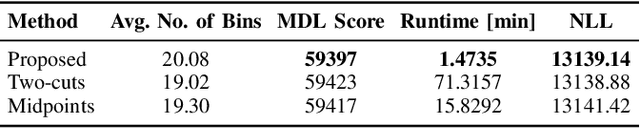
Abstract:Reliable density estimation is fundamental for numerous applications in statistics and machine learning. In many practical scenarios, data are best modeled as mixtures of component densities that capture complex and multimodal patterns. However, conventional density estimators based on uniform histograms often fail to capture local variations, especially when the underlying distribution is highly nonuniform. Furthermore, the inherent discontinuity of histograms poses challenges for tasks requiring smooth derivatives, such as gradient-based optimization, clustering, and nonparametric discriminant analysis. In this work, we present a novel non-parametric approach for multivariate probability density function (PDF) estimation that utilizes minimum description length (MDL)-based binning with quantile cuts. Our approach builds upon tensor factorization techniques, leveraging the canonical polyadic decomposition (CPD) of a joint probability tensor. We demonstrate the effectiveness of our method on synthetic data and a challenging real dry bean classification dataset.
Probabilistic Position-Aided Beam Selection for mmWave MIMO Systems
Apr 07, 2025

Abstract:Millimeter-wave (mmWave) MIMO systems rely on highly directional beamforming to overcome severe path loss and ensure robust communication links. However, selecting the optimal beam pair efficiently remains a challenge due to the large search space and the overhead of conventional methods. This paper proposes a probabilistic position-aided beam selection approach that exploits the statistical dependence between user equipment (UE) positions and optimal beam indices. We model the underlying joint probability mass function (PMF) of the positions and the beam indices as a low-rank tensor and estimate its parameters from training data using Bayesian inference. The estimated model is then used to predict the best (or a list of the top) beam pair indices for new UE positions. The proposed method is evaluated using data generated from a state-of-the-art ray tracing simulator and compared with neural network-based and fingerprinting approaches. The results show that our approach achieves a high data rate with fewer training samples and a significantly reduced beam search space. These advantages render it a promising solution for practical mmWave MIMO deployments, reducing the beam search overhead while maintaining a reliable connectivity.
Bayesian Estimation and Tuning-Free Rank Detection for Probability Mass Function Tensors
Oct 08, 2024Abstract:Obtaining a reliable estimate of the joint probability mass function (PMF) of a set of random variables from observed data is a significant objective in statistical signal processing and machine learning. Modelling the joint PMF as a tensor that admits a low-rank canonical polyadic decomposition (CPD) has enabled the development of efficient PMF estimation algorithms. However, these algorithms require the rank (model order) of the tensor to be specified beforehand. In real-world applications, the true rank is unknown. Therefore, an appropriate rank is usually selected from a candidate set either by observing validation errors or by computing various likelihood-based information criteria, a procedure which is computationally expensive for large datasets. This paper presents a novel Bayesian framework for estimating the joint PMF and automatically inferring its rank from observed data. We specify a Bayesian PMF estimation model and employ appropriate prior distributions for the model parameters, allowing for tuning-free rank inference via a single training run. We then derive a deterministic solution based on variational inference (VI) to approximate the posterior distributions of various model parameters. Additionally, we develop a scalable version of the VI-based approach by leveraging stochastic variational inference (SVI) to arrive at an efficient algorithm whose complexity scales sublinearly with the size of the dataset. Numerical experiments involving both synthetic data and real movie recommendation data illustrate the advantages of our VI and SVI-based methods in terms of estimation accuracy, automatic rank detection, and computational efficiency.
Time-Domain Based Embeddings for Spoofed Audio Representation
Oct 27, 2022



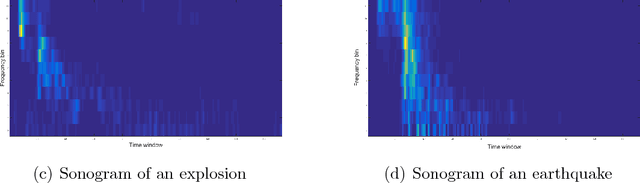
Abstract:Anti-spoofing is the task of speech authentication. That is, identifying genuine human speech compared to spoofed speech. The main focus of this paper is to suggest new representations for genuine and spoofed speech, based on the probability mass function (PMF) estimation of the audio waveforms' amplitude. We introduce a new feature extraction method for speech audio signals: unlike traditional methods, our method is based on direct processing of time-domain audio samples. The PMF is utilized by designing a feature extractor based on different PMF distances and similarity measures. As an additional step, we used filter-bank preprocessing, which significantly affects the discriminative characteristics of the features and facilitates convenient visualization of possible clustering of spoofing attacks. Furthermore, we use diffusion maps to reveal the underlying manifold on which the data lies. The suggested embeddings allow the use of simple linear separators to achieve decent performance. In addition, we present a convenient way to visualize the data, which helps to assess the efficiency of different spoofing techniques. The experimental results show the potential of using multi-channel PMF based features for the anti-spoofing task, in addition to the benefits of using diffusion maps both as an analysis tool and as an embedding tool.
Kernel Scaling for Manifold Learning and Classification
Jul 04, 2017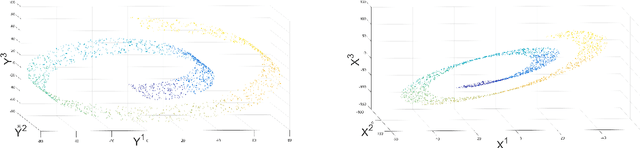
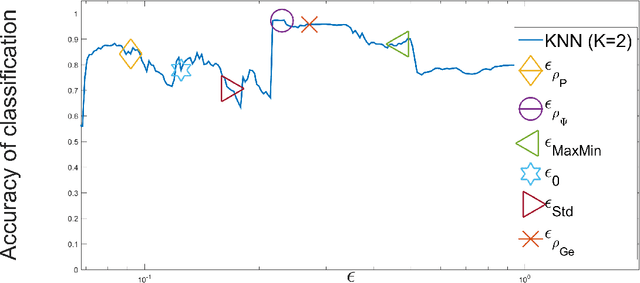
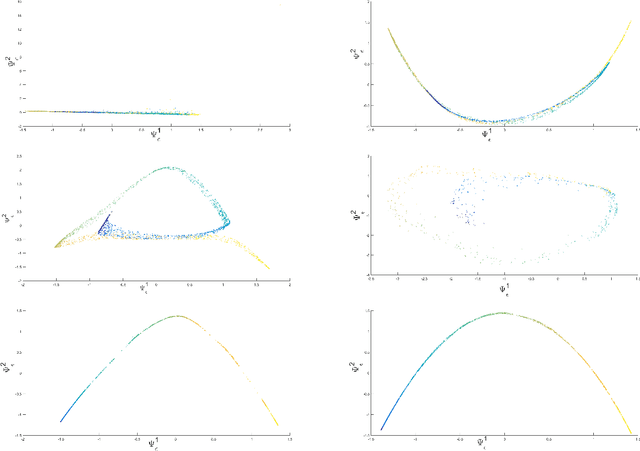
Abstract:Kernel methods play a critical role in many dimensionality reduction algorithms. They are useful in manifold learning, classification, clustering and other machine learning tasks. Setting the kernel's scale parameter, also referred as the kernel's bandwidth, highly affects the extracted low-dimensional representation. We propose to set a scale parameter that is tailored to the desired application such as classification and manifold learning. The scale computation for the manifold learning task enables that the dimension of the extracted embedding equals the intrinsic dimension estimation. Three methods are proposed for scale computation in a classification task. The proposed frameworks are simulated on artificial and real datasets. The results show a high correlation between optimal classification rates and the computed scaling.
MultiView Diffusion Maps
Mar 06, 2017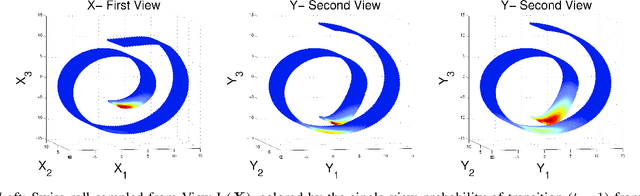
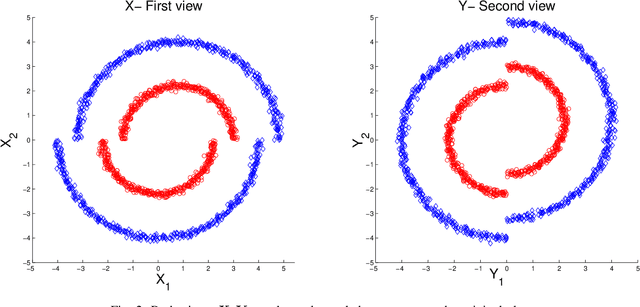
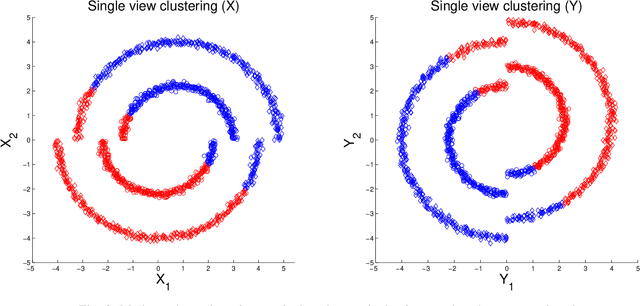
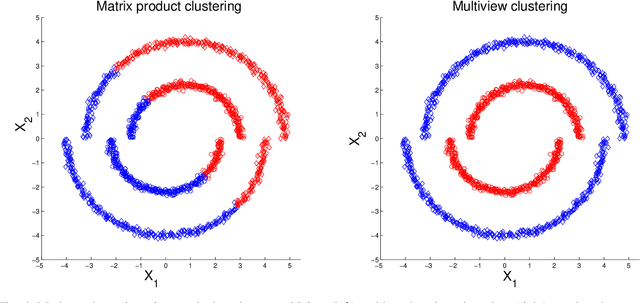
Abstract:In this study we consider learning a reduced dimensionality representation from datasets obtained under multiple views. Such multiple views of datasets can be obtained, for example, when the same underlying process is observed using several different modalities, or measured with different instrumentation. Our goal is to effectively exploit the availability of such multiple views for various purposes, such as non-linear embedding, manifold learning, spectral clustering, anomaly detection and non-linear system identification. Our proposed method exploits the intrinsic relation within each view, as well as the mutual relations between views. We do this by defining a cross-view model, in which an implied Random Walk process between objects is restrained to hop between the different views. Our method is robust to scaling of each dataset, and is insensitive to small structural changes in the data. Within this framework, we define new diffusion distances and analyze the spectra of the implied kernels. We demonstrate the applicability of the proposed approach on both artificial and real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge