Kernel Scaling for Manifold Learning and Classification

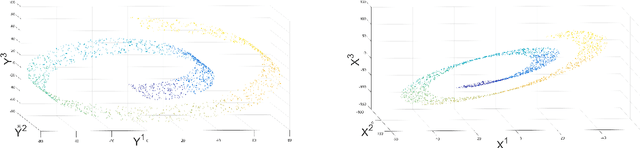
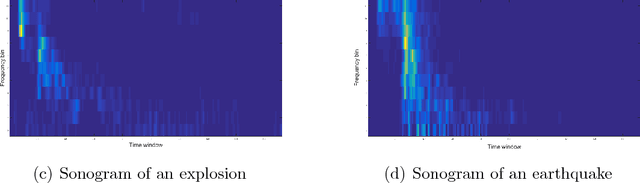
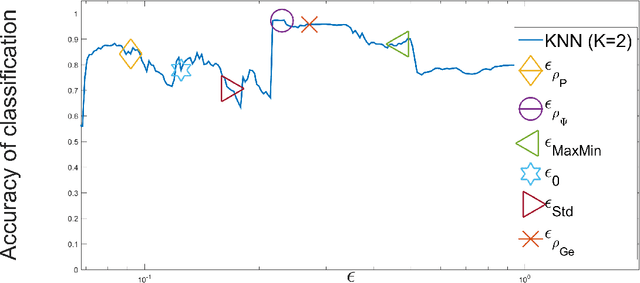
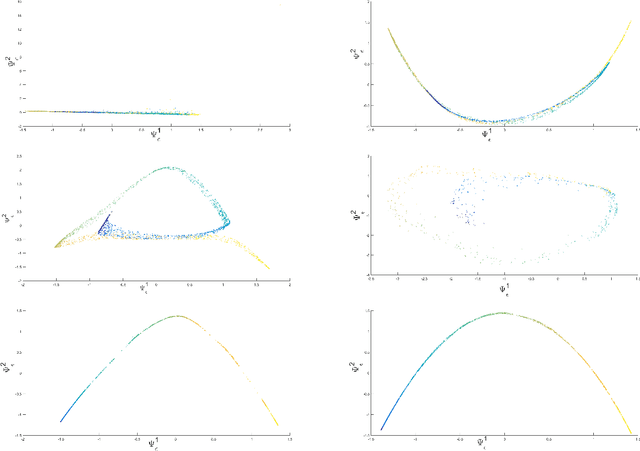
Kernel methods play a critical role in many dimensionality reduction algorithms. They are useful in manifold learning, classification, clustering and other machine learning tasks. Setting the kernel's scale parameter, also referred as the kernel's bandwidth, highly affects the extracted low-dimensional representation. We propose to set a scale parameter that is tailored to the desired application such as classification and manifold learning. The scale computation for the manifold learning task enables that the dimension of the extracted embedding equals the intrinsic dimension estimation. Three methods are proposed for scale computation in a classification task. The proposed frameworks are simulated on artificial and real datasets. The results show a high correlation between optimal classification rates and the computed scaling.