MultiView Diffusion Maps

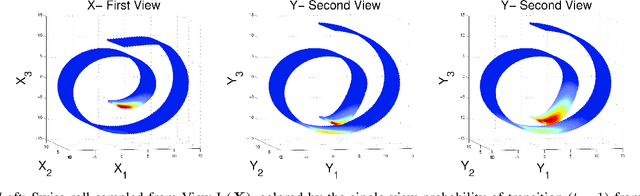
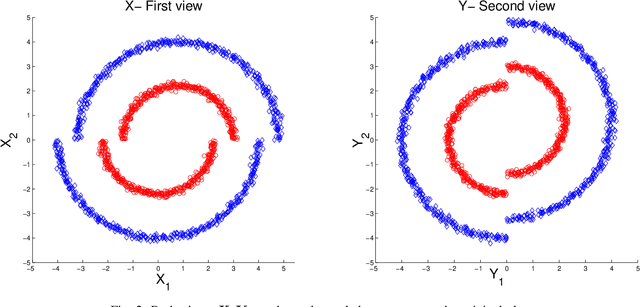
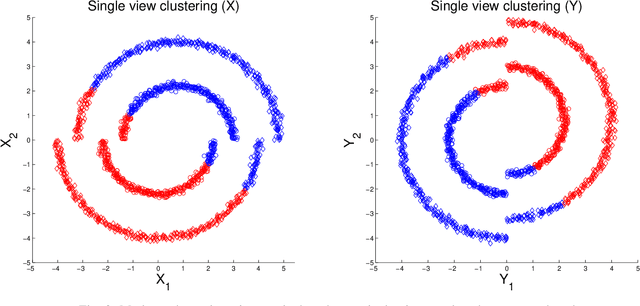
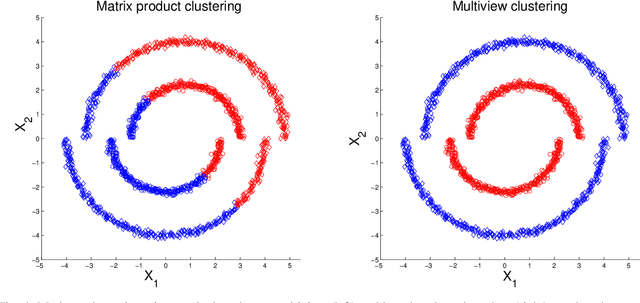
In this study we consider learning a reduced dimensionality representation from datasets obtained under multiple views. Such multiple views of datasets can be obtained, for example, when the same underlying process is observed using several different modalities, or measured with different instrumentation. Our goal is to effectively exploit the availability of such multiple views for various purposes, such as non-linear embedding, manifold learning, spectral clustering, anomaly detection and non-linear system identification. Our proposed method exploits the intrinsic relation within each view, as well as the mutual relations between views. We do this by defining a cross-view model, in which an implied Random Walk process between objects is restrained to hop between the different views. Our method is robust to scaling of each dataset, and is insensitive to small structural changes in the data. Within this framework, we define new diffusion distances and analyze the spectra of the implied kernels. We demonstrate the applicability of the proposed approach on both artificial and real data sets.