Amit Bermanis
Incomplete Pivoted QR-based Dimensionality Reduction
Jul 12, 2016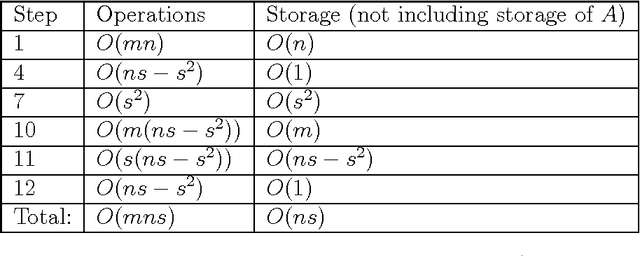
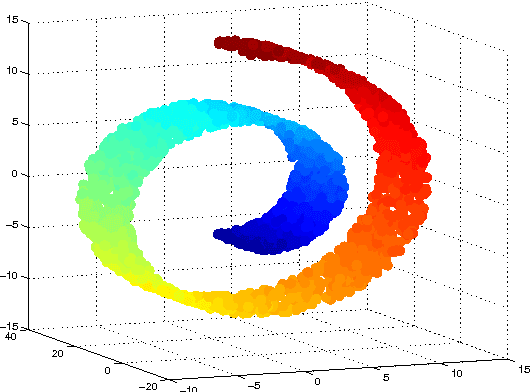
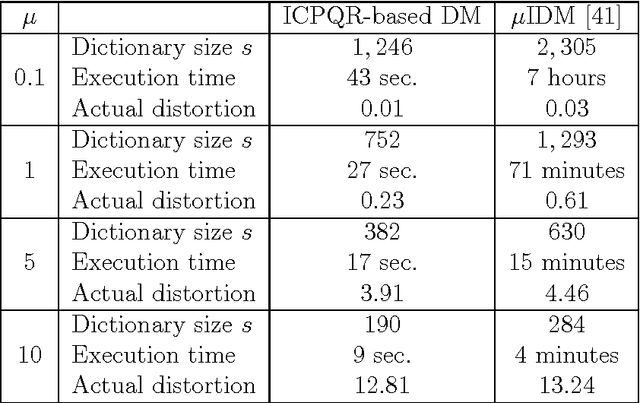
Abstract:High-dimensional big data appears in many research fields such as image recognition, biology and collaborative filtering. Often, the exploration of such data by classic algorithms is encountered with difficulties due to `curse of dimensionality' phenomenon. Therefore, dimensionality reduction methods are applied to the data prior to its analysis. Many of these methods are based on principal components analysis, which is statistically driven, namely they map the data into a low-dimension subspace that preserves significant statistical properties of the high-dimensional data. As a consequence, such methods do not directly address the geometry of the data, reflected by the mutual distances between multidimensional data point. Thus, operations such as classification, anomaly detection or other machine learning tasks may be affected. This work provides a dictionary-based framework for geometrically driven data analysis that includes dimensionality reduction, out-of-sample extension and anomaly detection. It embeds high-dimensional data in a low-dimensional subspace. This embedding preserves the original high-dimensional geometry of the data up to a user-defined distortion rate. In addition, it identifies a subset of landmark data points that constitute a dictionary for the analyzed dataset. The dictionary enables to have a natural extension of the low-dimensional embedding to out-of-sample data points, which gives rise to a distortion-based criterion for anomaly detection. The suggested method is demonstrated on synthetic and real-world datasets and achieves good results for classification, anomaly detection and out-of-sample tasks.
Diffusion Representations
Nov 19, 2015
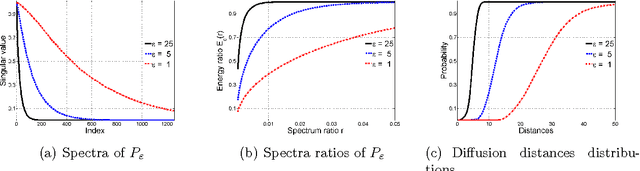
Abstract:Diffusion Maps framework is a kernel based method for manifold learning and data analysis that defines diffusion similarities by imposing a Markovian process on the given dataset. Analysis by this process uncovers the intrinsic geometric structures in the data. Recently, it was suggested to replace the standard kernel by a measure-based kernel that incorporates information about the density of the data. Thus, the manifold assumption is replaced by a more general measure-based assumption. The measure-based diffusion kernel incorporates two separate independent representations. The first determines a measure that correlates with a density that represents normal behaviors and patterns in the data. The second consists of the analyzed multidimensional data points. In this paper, we present a representation framework for data analysis of datasets that is based on a closed-form decomposition of the measure-based kernel. The proposed representation preserves pairwise diffusion distances that does not depend on the data size while being invariant to scale. For a stationary data, no out-of-sample extension is needed for embedding newly arrived data points in the representation space. Several aspects of the presented methodology are demonstrated on analytically generated data.
PCA-Based Out-of-Sample Extension for Dimensionality Reduction
Nov 03, 2015
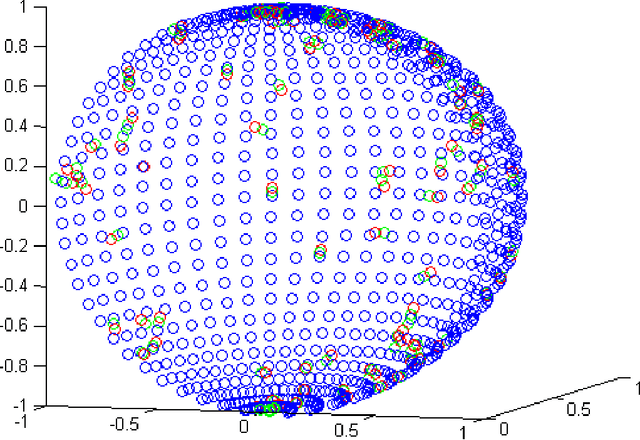

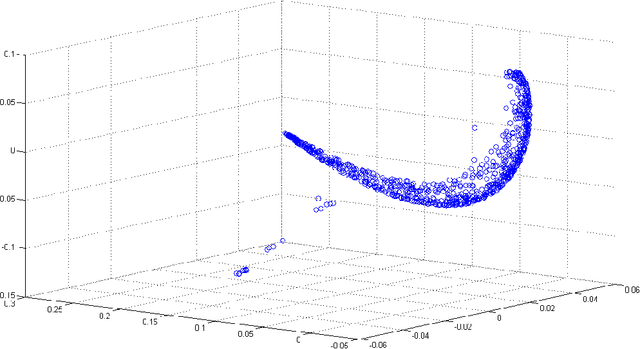
Abstract:Dimensionality reduction methods are very common in the field of high dimensional data analysis. Typically, algorithms for dimensionality reduction are computationally expensive. Therefore, their applications for the analysis of massive amounts of data are impractical. For example, repeated computations due to accumulated data are computationally prohibitive. In this paper, an out-of-sample extension scheme, which is used as a complementary method for dimensionality reduction, is presented. We describe an algorithm which performs an out-of-sample extension to newly-arrived data points. Unlike other extension algorithms such as Nystr\"om algorithm, the proposed algorithm uses the intrinsic geometry of the data and properties for dimensionality reduction map. We prove that the error of the proposed algorithm is bounded. Additionally to the out-of-sample extension, the algorithm provides a degree of the abnormality of any newly-arrived data point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge