Missing Entries Matrix Approximation and Completion
Paper and Code
Jun 29, 2014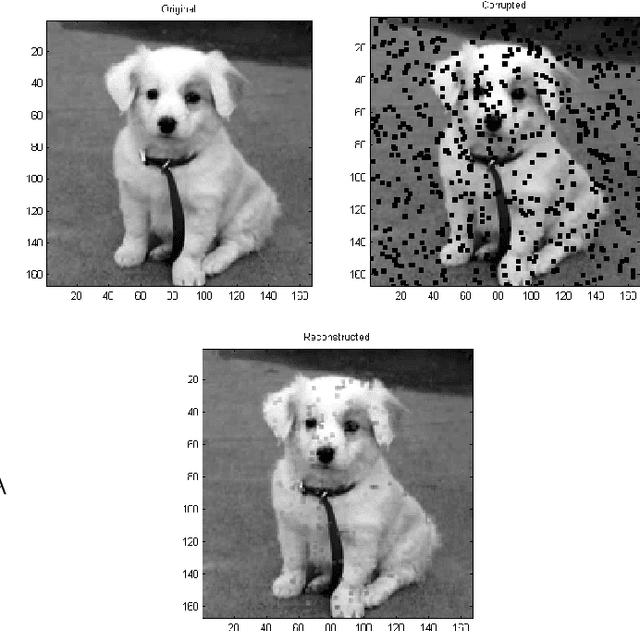
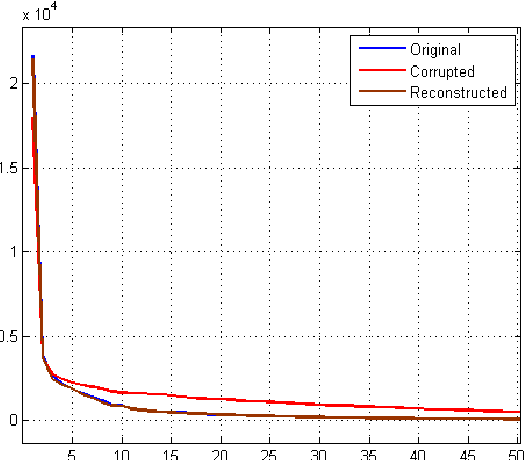
We describe several algorithms for matrix completion and matrix approximation when only some of its entries are known. The approximation constraint can be any whose approximated solution is known for the full matrix. For low rank approximations, similar algorithms appears recently in the literature under different names. In this work, we introduce new theorems for matrix approximation and show that these algorithms can be extended to handle different constraints such as nuclear norm, spectral norm, orthogonality constraints and more that are different than low rank approximations. As the algorithms can be viewed from an optimization point of view, we discuss their convergence to global solution for the convex case. We also discuss the optimal step size and show that it is fixed in each iteration. In addition, the derived matrix completion flow is robust and does not require any parameters. This matrix completion flow is applicable to different spectral minimizations and can be applied to physics, mathematics and electrical engineering problems such as data reconstruction of images and data coming from PDEs such as Helmholtz equation used for electromagnetic waves.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge