One scalar is all you need -- absolute depth estimation using monocular self-supervision

Self-supervised monocular depth estimators can be trained or fine-tuned on new scenes using only images and no ground-truth depth data, achieving good accuracy. However, these estimators suffer from the inherent ambiguity of the depth scale, significantly limiting their applicability. In this work, we present a method for transferring the depth-scale from existing source datasets collected with ground-truth depths to depth estimators that are trained using self-supervision on a newly collected target dataset consisting of images only, solving a significant limiting factor. We show that self-supervision based on projective geometry results in predicted depths that are linearly correlated with their ground-truth depths. Moreover, the linearity of this relationship also holds when jointly training on images from two different (real or synthetic) source and target domains. We utilize this observed property and model the relationship between the ground-truth and the predicted up-to-scale depths of images from the source domain using a single global scalar. Then, we scale the predicted up-to-scale depths of images from the target domain using the estimated global scaling factor, performing depth-scale transfer between the two domains. This suggested method was evaluated on the target KITTI and DDAD datasets, while using other real or synthetic source datasets, that have a larger field-of-view, other image style or structural content. Our approach achieves competitive accuracy on KITTI, even without using the specially tailored vKITTI or vKITTI2 datasets, and higher accuracy on DDAD, when using both real or synthetic source datasets.

Fast and Accurate Gaussian Kernel Ridge Regression Using Matrix Decompositions for Preconditioning

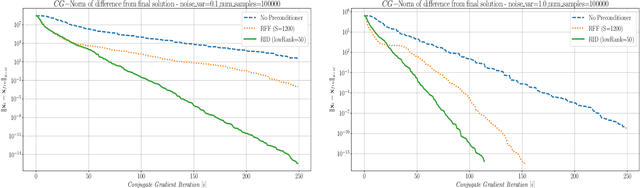
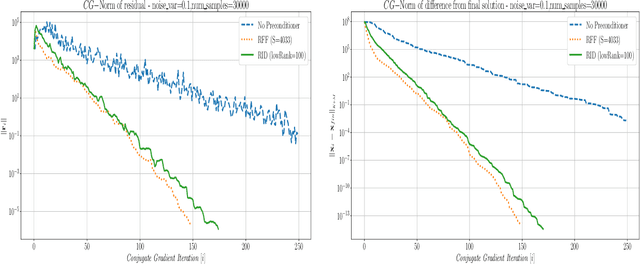
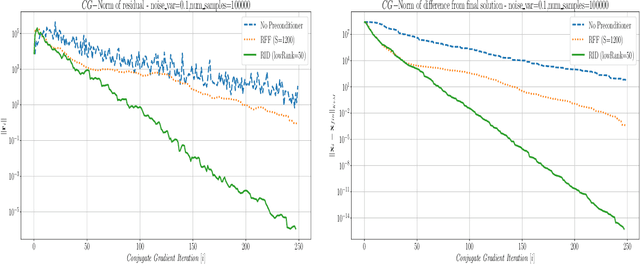
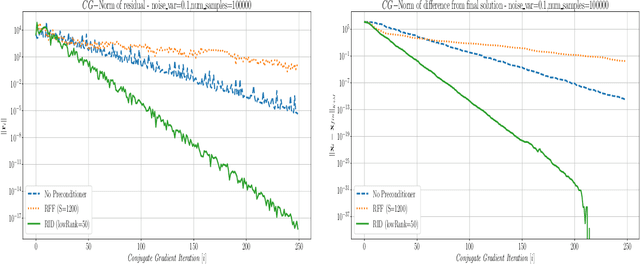
This paper presents a method for building a preconditioner for a kernel ridge regression problem, where the preconditioner is not only effective in its ability to reduce the condition number substantially, but also efficient in its application in terms of computational cost and memory consumption. The suggested approach is based on randomized matrix decomposition methods, combined with the fast multipole method to achieve an algorithm that can process large datasets in complexity linear to the number of data points. In addition, a detailed theoretical analysis is provided, including an upper bound to the condition number. Finally, for Gaussian kernels, the analysis shows that the required rank for a desired condition number can be determined directly from the dataset itself without performing any analysis on the kernel matrix.