ContraBAR: Contrastive Bayes-Adaptive Deep RL

In meta reinforcement learning (meta RL), an agent seeks a Bayes-optimal policy -- the optimal policy when facing an unknown task that is sampled from some known task distribution. Previous approaches tackled this problem by inferring a belief over task parameters, using variational inference methods. Motivated by recent successes of contrastive learning approaches in RL, such as contrastive predictive coding (CPC), we investigate whether contrastive methods can be used for learning Bayes-optimal behavior. We begin by proving that representations learned by CPC are indeed sufficient for Bayes optimality. Based on this observation, we propose a simple meta RL algorithm that uses CPC in lieu of variational belief inference. Our method, ContraBAR, achieves comparable performance to state-of-the-art in domains with state-based observation and circumvents the computational toll of future observation reconstruction, enabling learning in domains with image-based observations. It can also be combined with image augmentations for domain randomization and used seamlessly in both online and offline meta RL settings.

Fast and Accurate Gaussian Kernel Ridge Regression Using Matrix Decompositions for Preconditioning

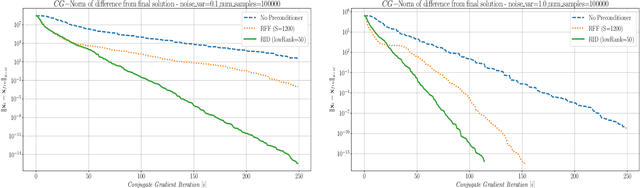
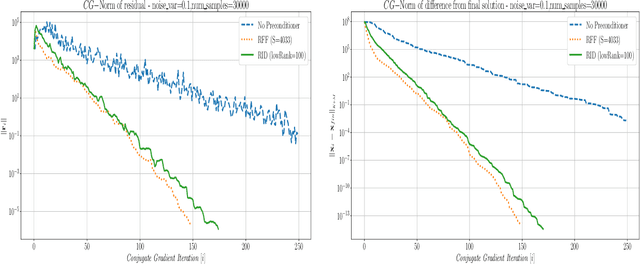
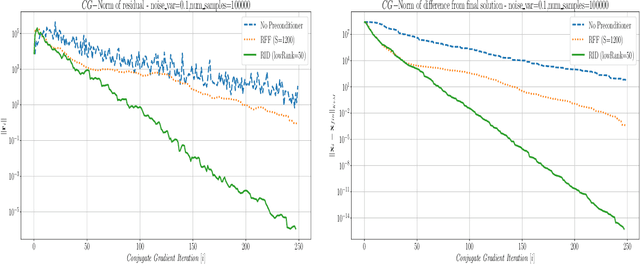
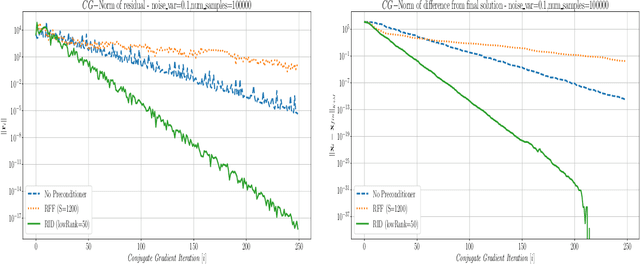
This paper presents a method for building a preconditioner for a kernel ridge regression problem, where the preconditioner is not only effective in its ability to reduce the condition number substantially, but also efficient in its application in terms of computational cost and memory consumption. The suggested approach is based on randomized matrix decomposition methods, combined with the fast multipole method to achieve an algorithm that can process large datasets in complexity linear to the number of data points. In addition, a detailed theoretical analysis is provided, including an upper bound to the condition number. Finally, for Gaussian kernels, the analysis shows that the required rank for a desired condition number can be determined directly from the dataset itself without performing any analysis on the kernel matrix.