Dynamic Reconstruction from Neuromorphic Data

Unlike traditional cameras which synchronously register pixel intensity, neuromorphic sensors only register `changes' at pixels where a change is occurring asynchronously. This enables neuromorphic sensors to sample at a micro-second level and efficiently capture the dynamics. Since, only sequences of asynchronous event changes are recorded rather than brightness intensities over time, many traditional image processing techniques cannot be directly applied. Furthermore, existing approaches, including the ones recently introduced by the authors, use traditional images combined with neuromorphic event data to carry out reconstructions. The aim of this work is introduce an optimization based approach to reconstruct images and dynamics only from the neuromoprhic event data without any additional knowledge of the events. Each pixel is modeled temporally. The experimental results on real data highlight the efficacy of the presented approach, paving the way for efficient and accurate processing of neuromorphic sensor data in real-world applications.

Mathematical Opportunities in Digital Twins (MATH-DT)

The report describes the discussions from the Workshop on Mathematical Opportunities in Digital Twins (MATH-DT) from December 11-13, 2023, George Mason University. It illustrates that foundational Mathematical advances are required for Digital Twins (DTs) that are different from traditional approaches. A traditional model, in biology, physics, engineering or medicine, starts with a generic physical law (e.g., equations) and is often a simplification of reality. A DT starts with a specific ecosystem, object or person (e.g., personalized care) representing reality, requiring multi -scale, -physics modeling and coupling. Thus, these processes begin at opposite ends of the simulation and modeling pipeline, requiring different reliability criteria and uncertainty assessments. Additionally, unlike existing approaches, a DT assists humans to make decisions for the physical system, which (via sensors) in turn feeds data into the DT, and operates for the life of the physical system. While some of the foundational mathematical research can be done without a specific application context, one must also keep specific applications in mind for DTs. E.g., modeling a bridge or a biological system (a patient), or a socio-technical system (a city) is very different. The models range from differential equations (deterministic/uncertain) in engineering, to stochastic in biology, including agent-based. These are multi-scale hybrid models or large scale (multi-objective) optimization problems under uncertainty. There are no universal models or approaches. For e.g., Kalman filters for forecasting might work in engineering, but can fail in biomedical domain. Ad hoc studies, with limited systematic work, have shown that AI/ML methods can fail for simple engineering systems and can work well for biomedical problems. A list of `Mathematical Opportunities and Challenges' concludes the report.

On-Manifold Projected Gradient Descent

This work provides a computable, direct, and mathematically rigorous approximation to the differential geometry of class manifolds for high-dimensional data, along with nonlinear projections from input space onto these class manifolds. The tools are applied to the setting of neural network image classifiers, where we generate novel, on-manifold data samples, and implement a projected gradient descent algorithm for on-manifold adversarial training. The susceptibility of neural networks (NNs) to adversarial attack highlights the brittle nature of NN decision boundaries in input space. Introducing adversarial examples during training has been shown to reduce the susceptibility of NNs to adversarial attack; however, it has also been shown to reduce the accuracy of the classifier if the examples are not valid examples for that class. Realistic "on-manifold" examples have been previously generated from class manifolds in the latent of an autoencoder. Our work explores these phenomena in a geometric and computational setting that is much closer to the raw, high-dimensional input space than can be provided by VAE or other black box dimensionality reductions. We employ conformally invariant diffusion maps (CIDM) to approximate class manifolds in diffusion coordinates, and develop the Nystr\"{o}m projection to project novel points onto class manifolds in this setting. On top of the manifold approximation, we leverage the spectral exterior calculus (SEC) to determine geometric quantities such as tangent vectors of the manifold. We use these tools to obtain adversarial examples that reside on a class manifold, yet fool a classifier. These misclassifications then become explainable in terms of human-understandable manipulations within the data, by expressing the on-manifold adversary in the semantic basis on the manifold.

GNEP Based Dynamic Segmentation and Motion Estimation for Neuromorphic Imaging

This paper explores the application of event-based cameras in the domains of image segmentation and motion estimation. These cameras offer a groundbreaking technology by capturing visual information as a continuous stream of asynchronous events, departing from the conventional frame-based image acquisition. We introduce a Generalized Nash Equilibrium based framework that leverages the temporal and spatial information derived from the event stream to carry out segmentation and velocity estimation. To establish the theoretical foundations, we derive an existence criteria and propose a multi-level optimization method for calculating equilibrium. The efficacy of this approach is shown through a series of experiments.

A Note on Dimensionality Reduction in Deep Neural Networks using Empirical Interpolation Method

Empirical interpolation method (EIM) is a well-known technique to efficiently approximate parameterized functions. This paper proposes to use EIM algorithm to efficiently reduce the dimension of the training data within supervised machine learning. This is termed as DNN-EIM. Applications in data science (e.g., MNIST) and parameterized (and time-dependent) partial differential equations (PDEs) are considered. The proposed DNNs in case of classification are trained in parallel for each class. This approach is sequential, i.e., new classes can be added without having to retrain the network. In case of PDEs, a DNN is designed corresponding to each EIM point. Again, these networks can be trained in parallel, for each EIM point. In all cases, the parallel networks require fewer than ten times the number of training weights. Significant gains are observed in terms of training times, without sacrificing accuracy.

Neural Network Representation of Time Integrators

Deep neural network (DNN) architectures are constructed that are the exact equivalent of explicit Runge-Kutta schemes for numerical time integration. The network weights and biases are given, i.e., no training is needed. In this way, the only task left for physics-based integrators is the DNN approximation of the right-hand side. This allows to clearly delineate the approximation estimates for right-hand side errors and time integration errors. The architecture required for the integration of a simple mass-damper-stiffness case is included as an example.

An Optimal Time Variable Learning Framework for Deep Neural Networks

Feature propagation in Deep Neural Networks (DNNs) can be associated to nonlinear discrete dynamical systems. The novelty, in this paper, lies in letting the discretization parameter (time step-size) vary from layer to layer, which needs to be learned, in an optimization framework. The proposed framework can be applied to any of the existing networks such as ResNet, DenseNet or Fractional-DNN. This framework is shown to help overcome the vanishing and exploding gradient issues. Stability of some of the existing continuous DNNs such as Fractional-DNN is also studied. The proposed approach is applied to an ill-posed 3D-Maxwell's equation.

NINNs: Nudging Induced Neural Networks

New algorithms called nudging induced neural networks (NINNs), to control and improve the accuracy of deep neural networks (DNNs), are introduced. The NINNs framework can be applied to almost all pre-existing DNNs, with forward propagation, with costs comparable to existing DNNs. NINNs work by adding a feedback control term to the forward propagation of the network. The feedback term nudges the neural network towards a desired quantity of interest. NINNs offer multiple advantages, for instance, they lead to higher accuracy when compared with existing data assimilation algorithms such as nudging. Rigorous convergence analysis is established for NINNs. The algorithmic and theoretical findings are illustrated on examples from data assimilation and chemically reacting flows.

Novel DNNs for Stiff ODEs with Applications to Chemically Reacting Flows

Chemically reacting flows are common in engineering, such as hypersonic flow, combustion, explosions, manufacturing processes and environmental assessments. For combustion, the number of reactions can be significant (over 100) and due to the very large CPU requirements of chemical reactions (over 99%) a large number of flow and combustion problems are presently beyond the capabilities of even the largest supercomputers. Motivated by this, novel Deep Neural Networks (DNNs) are introduced to approximate stiff ODEs. Two approaches are compared, i.e., either learn the solution or the derivative of the solution to these ODEs. These DNNs are applied to multiple species and reactions common in chemically reacting flows. Experimental results show that it is helpful to account for the physical properties of species while designing DNNs. The proposed approach is shown to generalize well.

Novel Deep neural networks for solving Bayesian statistical inverse

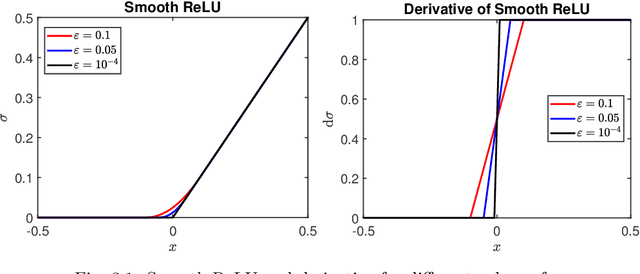
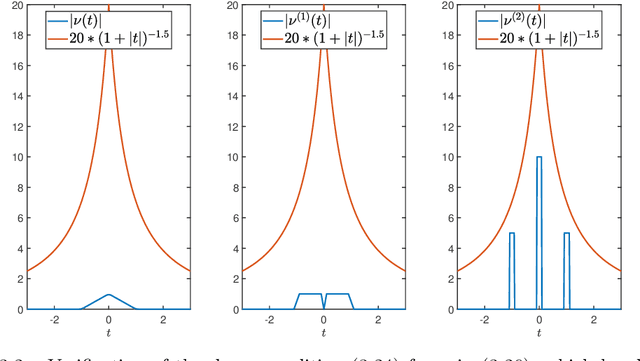
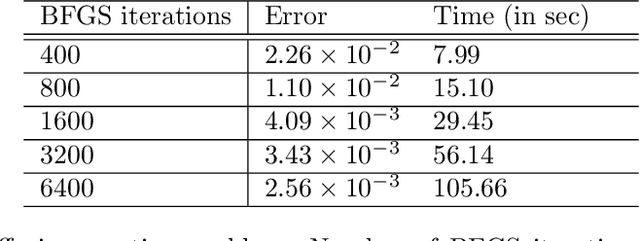
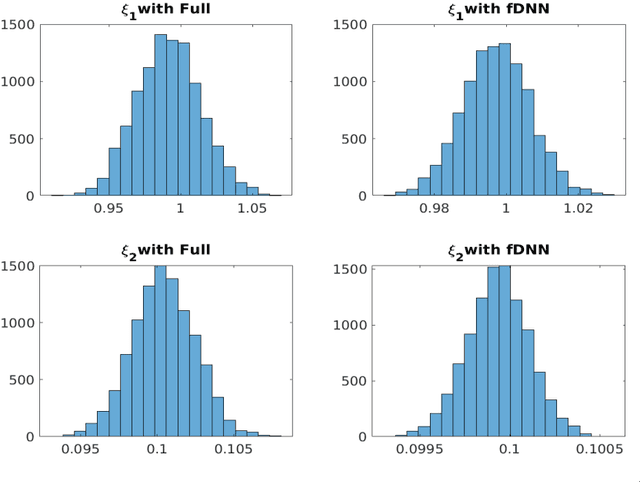
We consider the simulation of Bayesian statistical inverse problems governed by large-scale linear and nonlinear partial differential equations (PDEs). Markov chain Monte Carlo (MCMC) algorithms are standard techniques to solve such problems. However, MCMC techniques are computationally challenging as they require several thousands of forward PDE solves. The goal of this paper is to introduce a fractional deep neural network based approach for the forward solves within an MCMC routine. Moreover, we discuss some approximation error estimates and illustrate the efficiency of our approach via several numerical examples.