Novel Deep neural networks for solving Bayesian statistical inverse
Paper and Code
Feb 08, 2021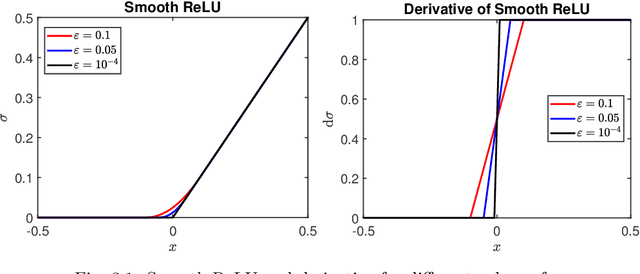
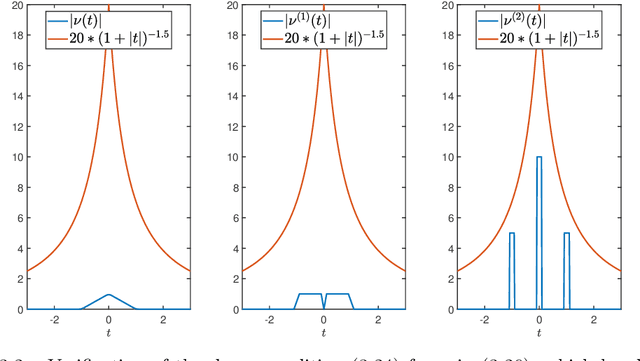
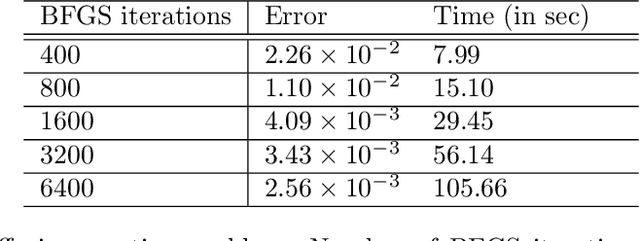
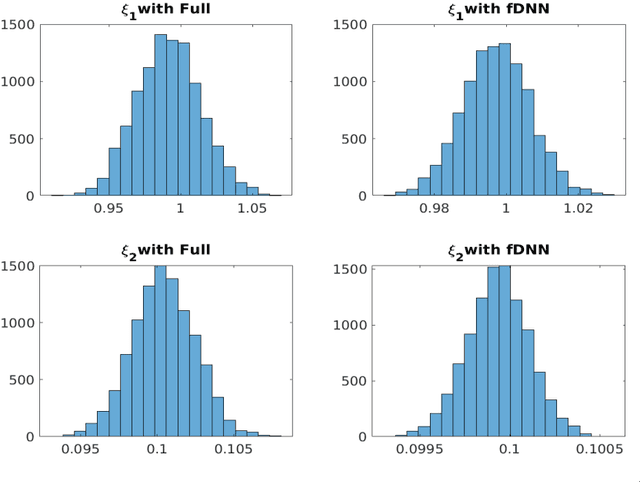
We consider the simulation of Bayesian statistical inverse problems governed by large-scale linear and nonlinear partial differential equations (PDEs). Markov chain Monte Carlo (MCMC) algorithms are standard techniques to solve such problems. However, MCMC techniques are computationally challenging as they require several thousands of forward PDE solves. The goal of this paper is to introduce a fractional deep neural network based approach for the forward solves within an MCMC routine. Moreover, we discuss some approximation error estimates and illustrate the efficiency of our approach via several numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge