Learning Control Policies of Hodgkin-Huxley Neuronal Dynamics

We present a neural network approach for closed-loop deep brain stimulation (DBS). We cast the problem of finding an optimal neurostimulation strategy as a control problem. In this setting, control policies aim to optimize therapeutic outcomes by tailoring the parameters of a DBS system, typically via electrical stimulation, in real time based on the patient's ongoing neuronal activity. We approximate the value function offline using a neural network to enable generating controls (stimuli) in real time via the feedback form. The neuronal activity is characterized by a nonlinear, stiff system of differential equations as dictated by the Hodgkin-Huxley model. Our training process leverages the relationship between Pontryagin's maximum principle and Hamilton-Jacobi-Bellman equations to update the value function estimates simultaneously. Our numerical experiments illustrate the accuracy of our approach for out-of-distribution samples and the robustness to moderate shocks and disturbances in the system.

Efficient Neural Network Approaches for Conditional Optimal Transport with Applications in Bayesian Inference

We present two neural network approaches that approximate the solutions of static and dynamic conditional optimal transport (COT) problems, respectively. Both approaches enable sampling and density estimation of conditional probability distributions, which are core tasks in Bayesian inference. Our methods represent the target conditional distributions as transformations of a tractable reference distribution and, therefore, fall into the framework of measure transport. COT maps are a canonical choice within this framework, with desirable properties such as uniqueness and monotonicity. However, the associated COT problems are computationally challenging, even in moderate dimensions. To improve the scalability, our numerical algorithms leverage neural networks to parameterize COT maps. Our methods exploit the structure of the static and dynamic formulations of the COT problem. PCP-Map models conditional transport maps as the gradient of a partially input convex neural network (PICNN) and uses a novel numerical implementation to increase computational efficiency compared to state-of-the-art alternatives. COT-Flow models conditional transports via the flow of a regularized neural ODE; it is slower to train but offers faster sampling. We demonstrate their effectiveness and efficiency by comparing them with state-of-the-art approaches using benchmark datasets and Bayesian inverse problems.

Novel DNNs for Stiff ODEs with Applications to Chemically Reacting Flows

Chemically reacting flows are common in engineering, such as hypersonic flow, combustion, explosions, manufacturing processes and environmental assessments. For combustion, the number of reactions can be significant (over 100) and due to the very large CPU requirements of chemical reactions (over 99%) a large number of flow and combustion problems are presently beyond the capabilities of even the largest supercomputers. Motivated by this, novel Deep Neural Networks (DNNs) are introduced to approximate stiff ODEs. Two approaches are compared, i.e., either learn the solution or the derivative of the solution to these ODEs. These DNNs are applied to multiple species and reactions common in chemically reacting flows. Experimental results show that it is helpful to account for the physical properties of species while designing DNNs. The proposed approach is shown to generalize well.

Novel Deep neural networks for solving Bayesian statistical inverse

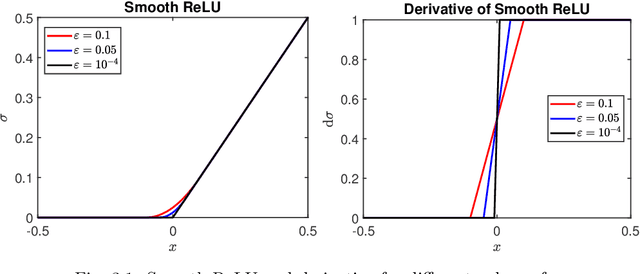
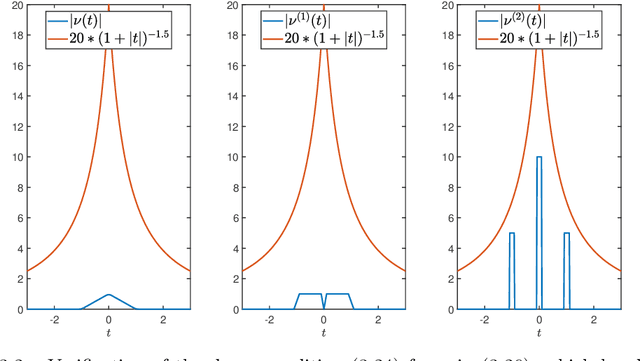
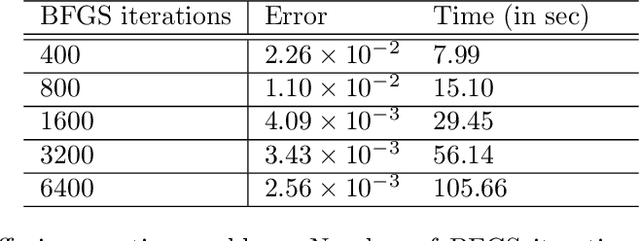
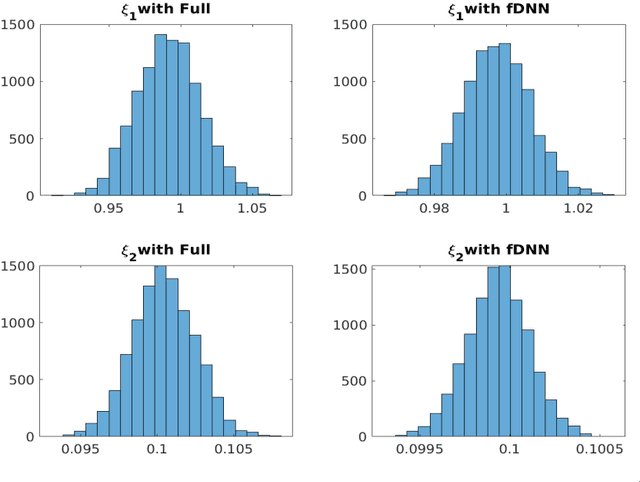
We consider the simulation of Bayesian statistical inverse problems governed by large-scale linear and nonlinear partial differential equations (PDEs). Markov chain Monte Carlo (MCMC) algorithms are standard techniques to solve such problems. However, MCMC techniques are computationally challenging as they require several thousands of forward PDE solves. The goal of this paper is to introduce a fractional deep neural network based approach for the forward solves within an MCMC routine. Moreover, we discuss some approximation error estimates and illustrate the efficiency of our approach via several numerical examples.

Fractional Deep Neural Network via Constrained Optimization

This paper introduces a novel algorithmic framework for a deep neural network (DNN), which in a mathematically rigorous manner, allows us to incorporate history (or memory) into the network -- it ensures all layers are connected to one another. This DNN, called Fractional-DNN, can be viewed as a time-discretization of a fractional in time nonlinear ordinary differential equation (ODE). The learning problem then is a minimization problem subject to that fractional ODE as constraints. We emphasize that an analogy between the existing DNN and ODEs, with standard time derivative, is well-known by now. The focus of our work is the Fractional-DNN. Using the Lagrangian approach, we provide a derivation of the backward propagation and the design equations. We test our network on several datasets for classification problems. Fractional-DNN offers various advantages over the existing DNN. The key benefits are a significant improvement to the vanishing gradient issue due to the memory effect, and better handling of nonsmooth data due to the network's ability to approximate non-smooth functions.