Fractional Deep Neural Network via Constrained Optimization

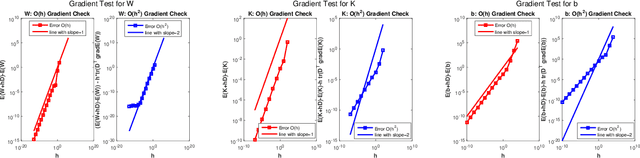
This paper introduces a novel algorithmic framework for a deep neural network (DNN), which in a mathematically rigorous manner, allows us to incorporate history (or memory) into the network -- it ensures all layers are connected to one another. This DNN, called Fractional-DNN, can be viewed as a time-discretization of a fractional in time nonlinear ordinary differential equation (ODE). The learning problem then is a minimization problem subject to that fractional ODE as constraints. We emphasize that an analogy between the existing DNN and ODEs, with standard time derivative, is well-known by now. The focus of our work is the Fractional-DNN. Using the Lagrangian approach, we provide a derivation of the backward propagation and the design equations. We test our network on several datasets for classification problems. Fractional-DNN offers various advantages over the existing DNN. The key benefits are a significant improvement to the vanishing gradient issue due to the memory effect, and better handling of nonsmooth data due to the network's ability to approximate non-smooth functions.

Bilevel Optimization, Deep Learning and Fractional Laplacian Regularization with Applications in Tomography

In this work we consider a generalized bilevel optimization framework for solving inverse problems. We introduce fractional Laplacian as a regularizer to improve the reconstruction quality, and compare it with the total variation regularization. We emphasize that the key advantage of using fractional Laplacian as a regularizer is that it leads to a linear operator, as opposed to the total variation regularization which results in a nonlinear degenerate operator. Inspired by residual neural networks, to learn the optimal strength of regularization and the exponent of fractional Laplacian, we develop a dedicated bilevel optimization neural network with a variable depth for a general regularized inverse problem. We also draw some parallels between an activation function in a neural network and regularization. We illustrate how to incorporate various regularizer choices into our proposed network. As an example, we consider tomographic reconstruction as a model problem and show an improvement in reconstruction quality, especially for limited data, via fractional Laplacian regularization. We successfully learn the regularization strength and the fractional exponent via our proposed bilevel optimization neural network. We observe that the fractional Laplacian regularization outperforms total variation regularization. This is specially encouraging, and important, in the case of limited and noisy data.