Neural Network Representation of Time Integrators

Deep neural network (DNN) architectures are constructed that are the exact equivalent of explicit Runge-Kutta schemes for numerical time integration. The network weights and biases are given, i.e., no training is needed. In this way, the only task left for physics-based integrators is the DNN approximation of the right-hand side. This allows to clearly delineate the approximation estimates for right-hand side errors and time integration errors. The architecture required for the integration of a simple mass-damper-stiffness case is included as an example.

NINNs: Nudging Induced Neural Networks

New algorithms called nudging induced neural networks (NINNs), to control and improve the accuracy of deep neural networks (DNNs), are introduced. The NINNs framework can be applied to almost all pre-existing DNNs, with forward propagation, with costs comparable to existing DNNs. NINNs work by adding a feedback control term to the forward propagation of the network. The feedback term nudges the neural network towards a desired quantity of interest. NINNs offer multiple advantages, for instance, they lead to higher accuracy when compared with existing data assimilation algorithms such as nudging. Rigorous convergence analysis is established for NINNs. The algorithmic and theoretical findings are illustrated on examples from data assimilation and chemically reacting flows.

Novel DNNs for Stiff ODEs with Applications to Chemically Reacting Flows

Chemically reacting flows are common in engineering, such as hypersonic flow, combustion, explosions, manufacturing processes and environmental assessments. For combustion, the number of reactions can be significant (over 100) and due to the very large CPU requirements of chemical reactions (over 99%) a large number of flow and combustion problems are presently beyond the capabilities of even the largest supercomputers. Motivated by this, novel Deep Neural Networks (DNNs) are introduced to approximate stiff ODEs. Two approaches are compared, i.e., either learn the solution or the derivative of the solution to these ODEs. These DNNs are applied to multiple species and reactions common in chemically reacting flows. Experimental results show that it is helpful to account for the physical properties of species while designing DNNs. The proposed approach is shown to generalize well.

Fractional Deep Neural Network via Constrained Optimization

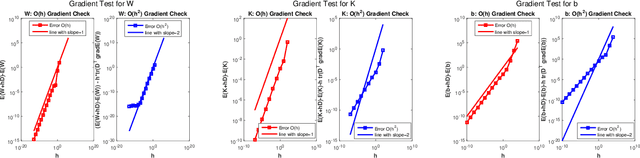
This paper introduces a novel algorithmic framework for a deep neural network (DNN), which in a mathematically rigorous manner, allows us to incorporate history (or memory) into the network -- it ensures all layers are connected to one another. This DNN, called Fractional-DNN, can be viewed as a time-discretization of a fractional in time nonlinear ordinary differential equation (ODE). The learning problem then is a minimization problem subject to that fractional ODE as constraints. We emphasize that an analogy between the existing DNN and ODEs, with standard time derivative, is well-known by now. The focus of our work is the Fractional-DNN. Using the Lagrangian approach, we provide a derivation of the backward propagation and the design equations. We test our network on several datasets for classification problems. Fractional-DNN offers various advantages over the existing DNN. The key benefits are a significant improvement to the vanishing gradient issue due to the memory effect, and better handling of nonsmooth data due to the network's ability to approximate non-smooth functions.