Mean Subtraction and Mode Selection in Dynamic Mode Decomposition

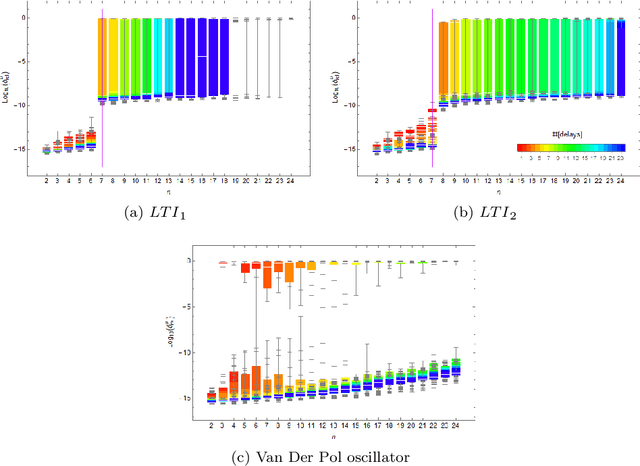
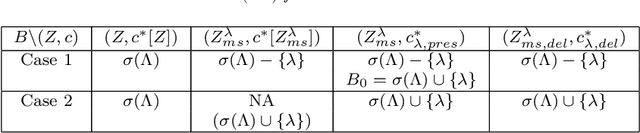
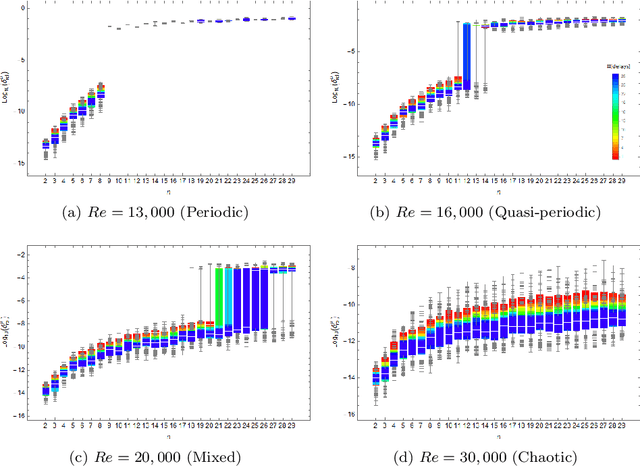
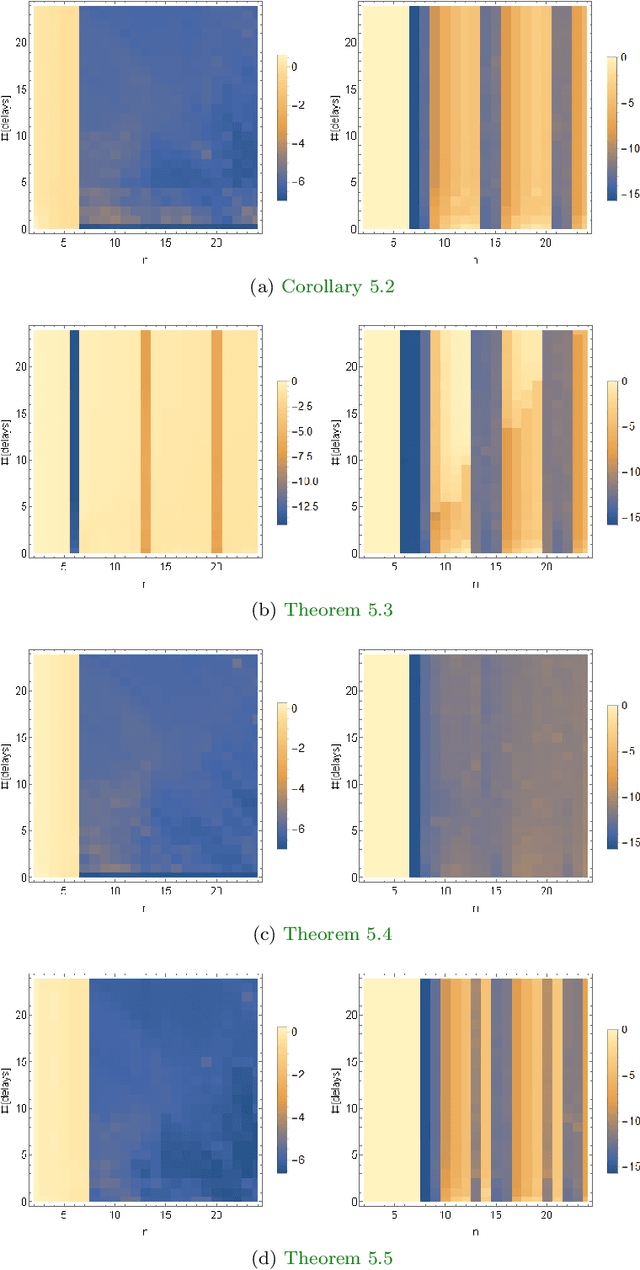
Koopman mode analysis has provided a framework for analysis of nonlinear phenomena across a plethora of fields. Its numerical implementation via Dynamic Mode Decomposition (DMD) has been extensively deployed and improved upon over the last decade. We address the problems of mean subtraction and DMD mode selection in the context of finite dimensional Koopman invariant subspaces. Preprocessing of data by subtraction of the temporal mean of a time series has been a point of contention in companion matrix-based DMD. This stems from the potential of said preprocessing to render DMD equivalent to temporal DFT. We prove that this equivalence is impossible when the order of the DMD-based representation of the dynamics exceeds the dimension of the system. Moreover, this parity of DMD and DFT is mostly indicative of an inadequacy of data, in the sense that the number of snapshots taken is not enough to represent the true dynamics of the system. We then vindicate the practice of pruning DMD eigenvalues based on the norm of the respective modes. Once a minimum number of time delays has been taken, DMD eigenvalues corresponding to DMD modes with low norm are shown to be spurious, and hence must be discarded. When dealing with mean-subtracted data, the above criterion for detecting synthetic eigenvalues can be applied after additional pre-processing. This takes the form of an eigenvalue constraint on Companion DMD, or yet another time delay.

Coarse-grained and emergent distributed parameter systems from data

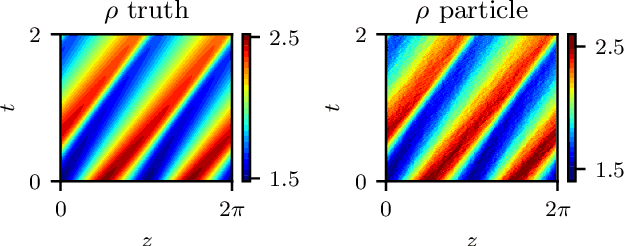
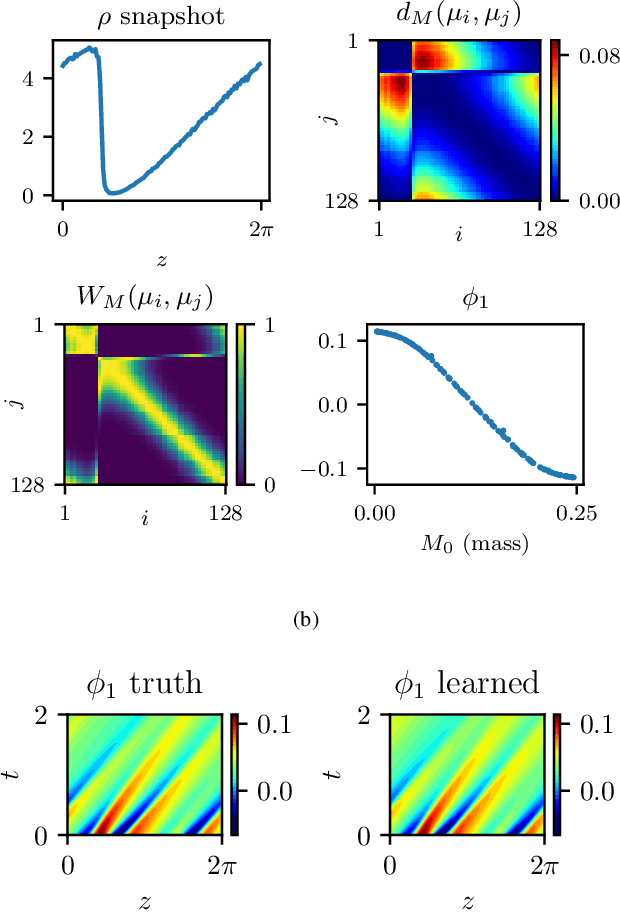
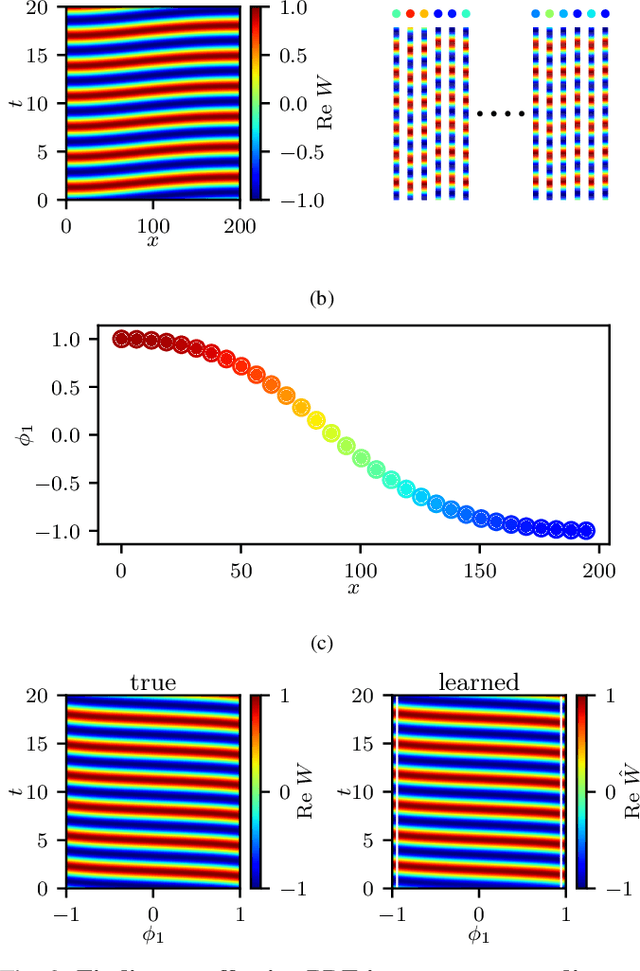
We explore the derivation of distributed parameter system evolution laws (and in particular, partial differential operators and associated partial differential equations, PDEs) from spatiotemporal data. This is, of course, a classical identification problem; our focus here is on the use of manifold learning techniques (and, in particular, variations of Diffusion Maps) in conjunction with neural network learning algorithms that allow us to attempt this task when the dependent variables, and even the independent variables of the PDE are not known a priori and must be themselves derived from the data. The similarity measure used in Diffusion Maps for dependent coarse variable detection involves distances between local particle distribution observations; for independent variable detection we use distances between local short-time dynamics. We demonstrate each approach through an illustrative established PDE example. Such variable-free, emergent space identification algorithms connect naturally with equation-free multiscale computation tools.

Particles to Partial Differential Equations Parsimoniously

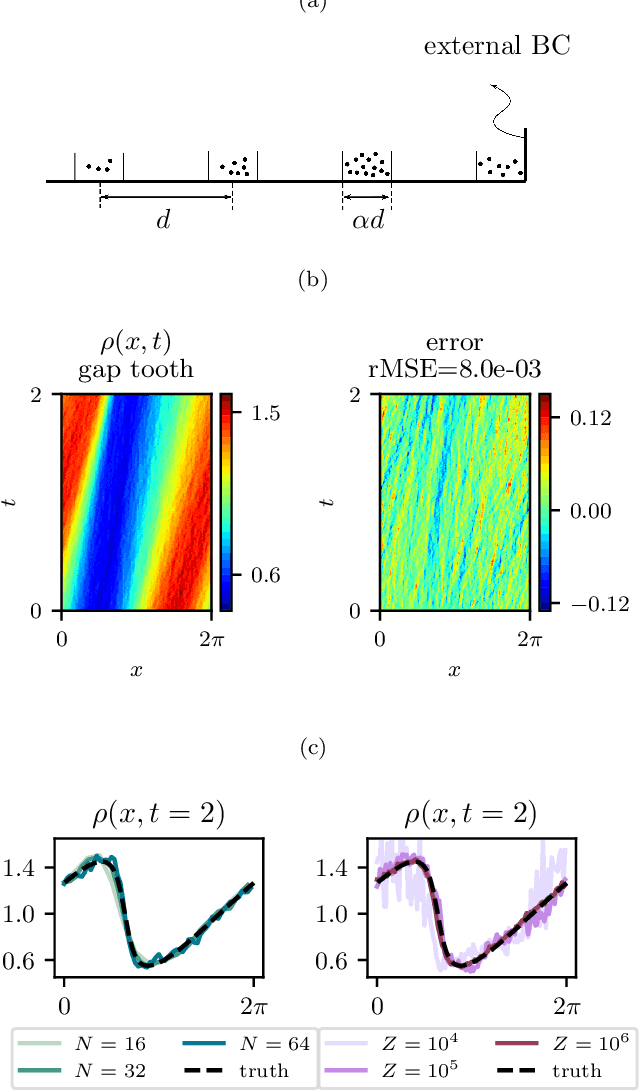
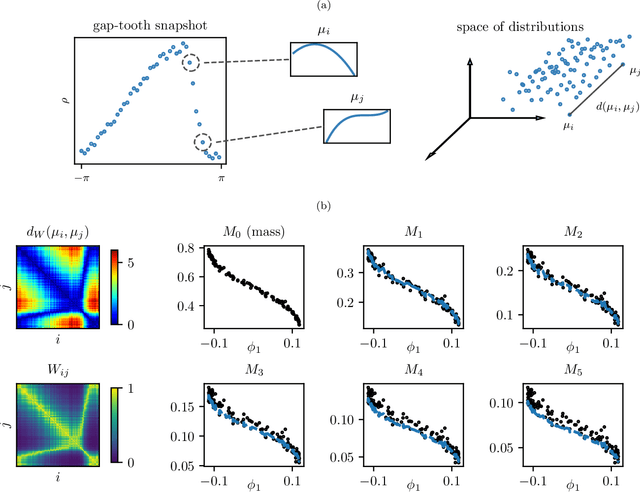
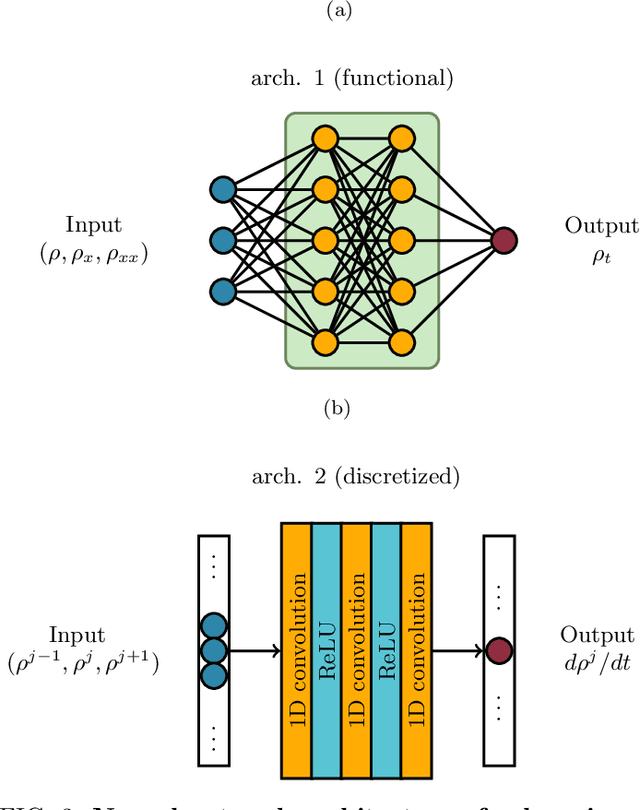
Equations governing physico-chemical processes are usually known at microscopic spatial scales, yet one suspects that there exist equations, e.g. in the form of Partial Differential Equations (PDEs), that can explain the system evolution at much coarser, meso- or macroscopic length scales. Discovering those coarse-grained effective PDEs can lead to considerable savings in computation-intensive tasks like prediction or control. We propose a framework combining artificial neural networks with multiscale computation, in the form of equation-free numerics, for efficient discovery of such macro-scale PDEs directly from microscopic simulations. Gathering sufficient microscopic data for training neural networks can be computationally prohibitive; equation-free numerics enable a more parsimonious collection of training data by only operating in a sparse subset of the space-time domain. We also propose using a data-driven approach, based on manifold learning and unnormalized optimal transport of distributions, to identify macro-scale dependent variable(s) suitable for the data-driven discovery of said PDEs. This approach can corroborate physically motivated candidate variables, or introduce new data-driven variables, in terms of which the coarse-grained effective PDE can be formulated. We illustrate our approach by extracting coarse-grained evolution equations from particle-based simulations with a priori unknown macro-scale variable(s), while significantly reducing the requisite data collection computational effort.

Search strategy in a complex and dynamic environment: the MH370 case

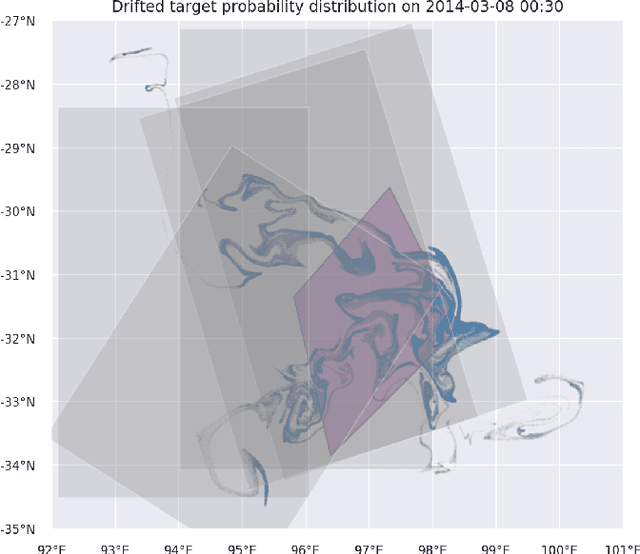
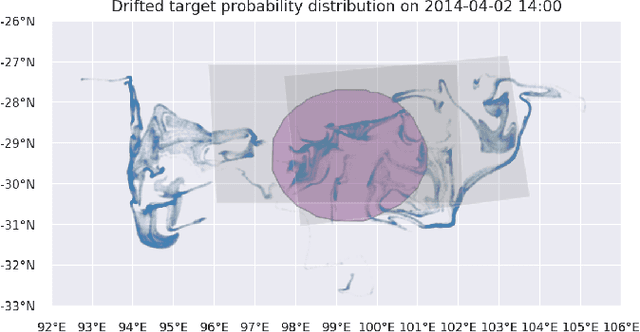
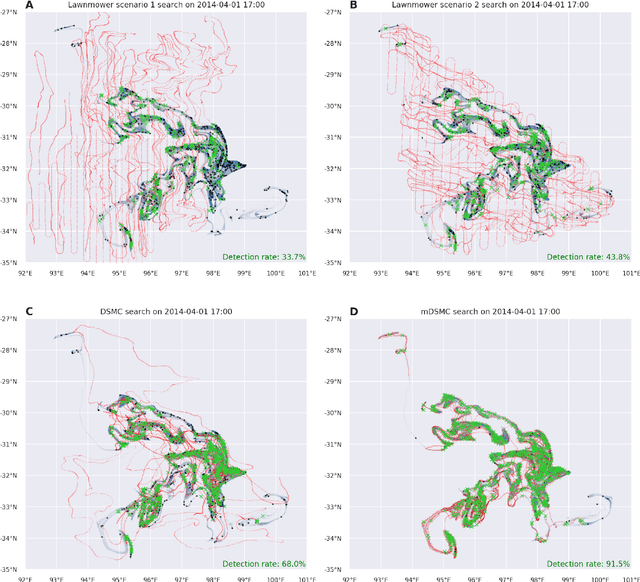
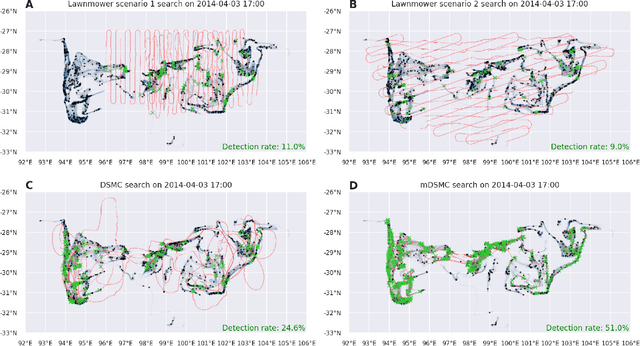
Search and detection of objects on the ocean surface is a challenging task due to the complexity of the drift dynamics and lack of known optimal solutions for the path of the search agents. This challenge was highlighted by the unsuccessful search for Malaysian Flight 370 (MH370) which disappeared on March 8, 2014. In this paper, we propose an improvement of a search algorithm rooted in the ergodic theory of dynamical systems which can accommodate complex geometries and uncertainties of the drifting search areas on the ocean surface. We illustrate the effectiveness of this algorithm in a computational replication of the conducted search for MH370. In comparison to conventional search methods, the proposed algorithm leads to an order of magnitude improvement in success rate over the time period of the actual search operation. Simulations of the proposed search control also indicate that the initial success rate of finding debris increases in the event of delayed search commencement. This is due to the existence of convergence zones in the search area which leads to local aggregation of debris in those zones and hence reduction of the effective size of the area to be searched.