Mean Subtraction and Mode Selection in Dynamic Mode Decomposition

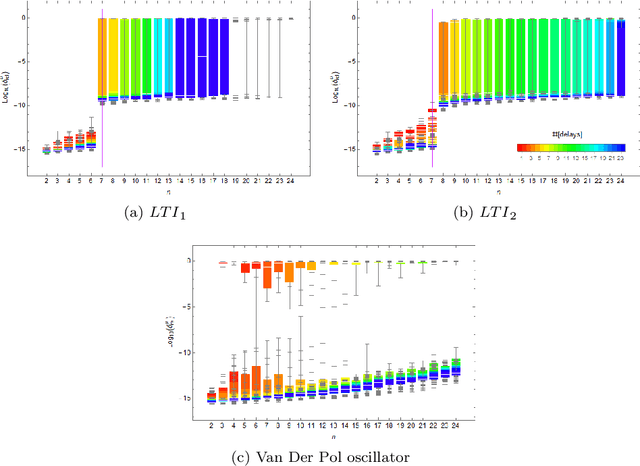
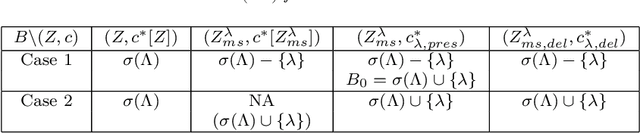
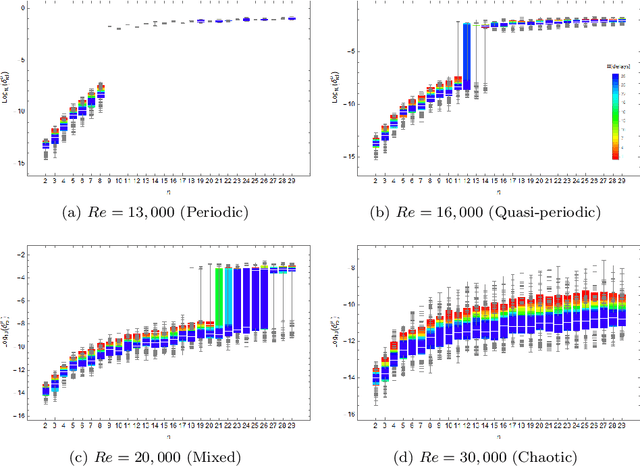
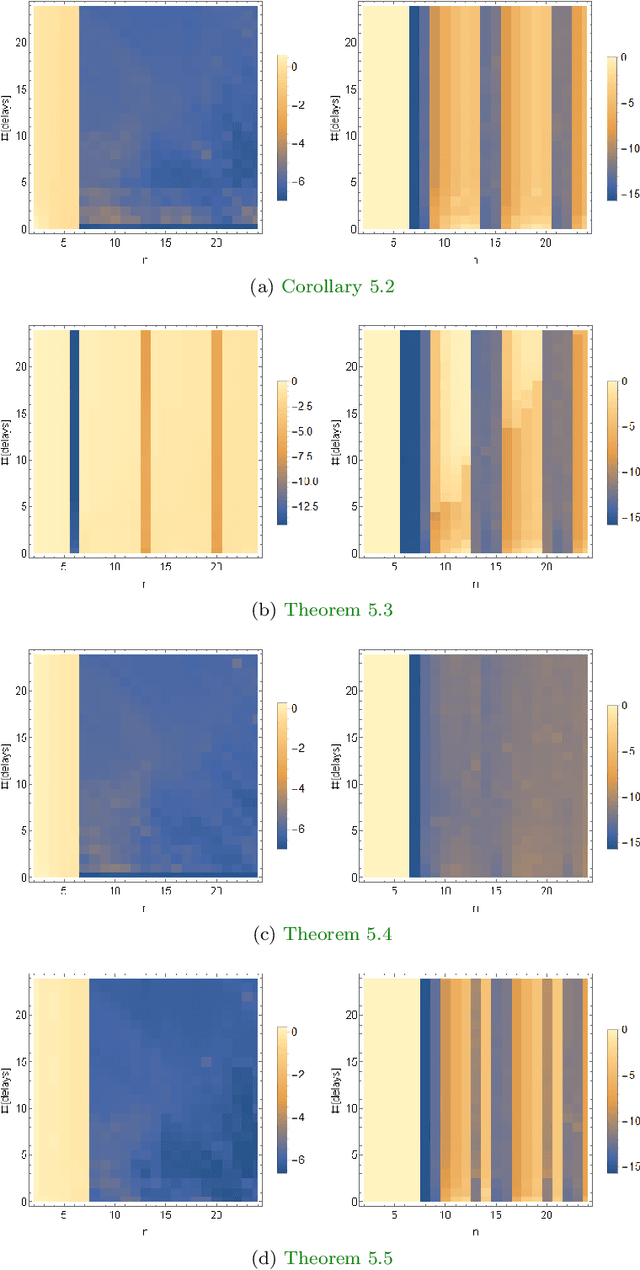
Koopman mode analysis has provided a framework for analysis of nonlinear phenomena across a plethora of fields. Its numerical implementation via Dynamic Mode Decomposition (DMD) has been extensively deployed and improved upon over the last decade. We address the problems of mean subtraction and DMD mode selection in the context of finite dimensional Koopman invariant subspaces. Preprocessing of data by subtraction of the temporal mean of a time series has been a point of contention in companion matrix-based DMD. This stems from the potential of said preprocessing to render DMD equivalent to temporal DFT. We prove that this equivalence is impossible when the order of the DMD-based representation of the dynamics exceeds the dimension of the system. Moreover, this parity of DMD and DFT is mostly indicative of an inadequacy of data, in the sense that the number of snapshots taken is not enough to represent the true dynamics of the system. We then vindicate the practice of pruning DMD eigenvalues based on the norm of the respective modes. Once a minimum number of time delays has been taken, DMD eigenvalues corresponding to DMD modes with low norm are shown to be spurious, and hence must be discarded. When dealing with mean-subtracted data, the above criterion for detecting synthetic eigenvalues can be applied after additional pre-processing. This takes the form of an eigenvalue constraint on Companion DMD, or yet another time delay.