Black and Gray Box Learning of Amplitude Equations: Application to Phase Field Systems

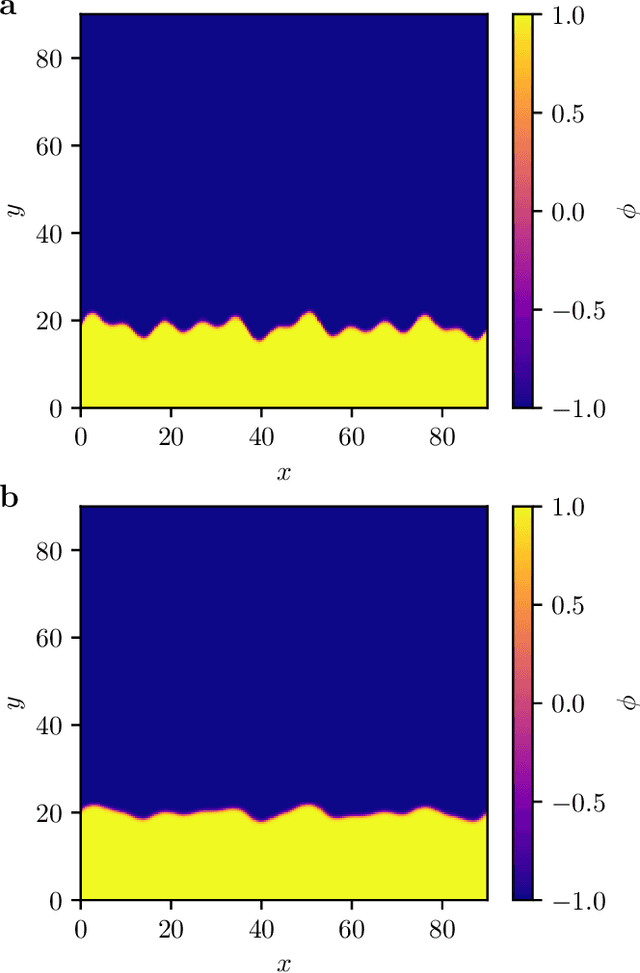
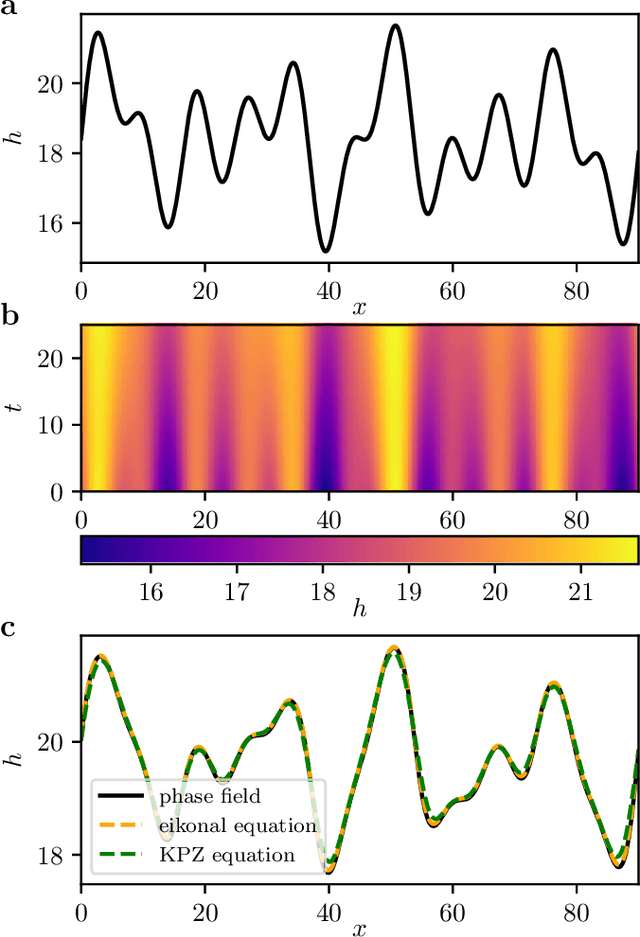
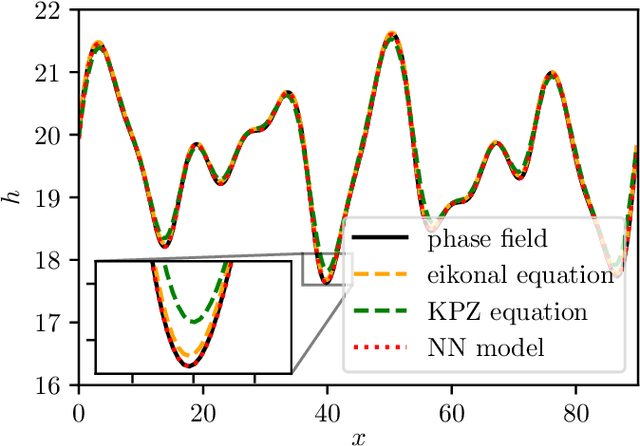
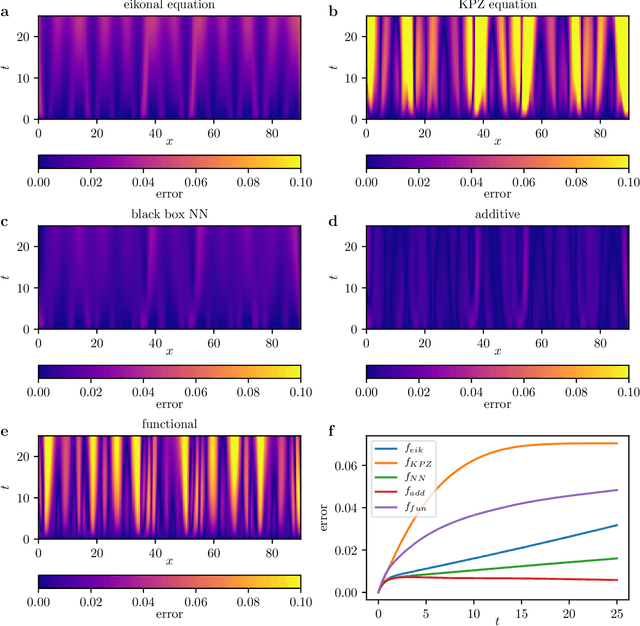
We present a data-driven approach to learning surrogate models for amplitude equations, and illustrate its application to interfacial dynamics of phase field systems. In particular, we demonstrate learning effective partial differential equations describing the evolution of phase field interfaces from full phase field data. We illustrate this on a model phase field system, where analytical approximate equations for the dynamics of the phase field interface (a higher order eikonal equation and its approximation, the Kardar-Parisi-Zhang (KPZ) equation) are known. For this system, we discuss data-driven approaches for the identification of equations that accurately describe the front interface dynamics. When the analytical approximate models mentioned above become inaccurate, as we move beyond the region of validity of the underlying assumptions, the data-driven equations outperform them. In these regimes, going beyond black-box identification, we explore different approaches to learn data-driven corrections to the analytically approximate models, leading to effective gray box partial differential equations.

Initializing LSTM internal states via manifold learning

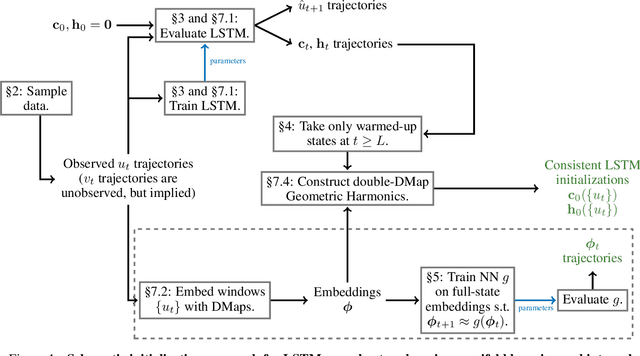
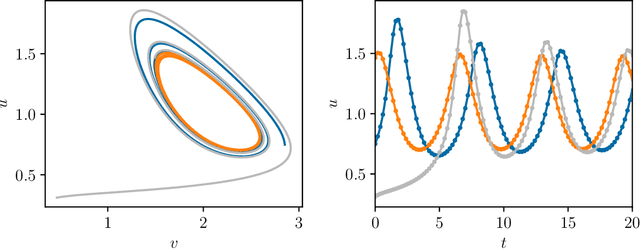
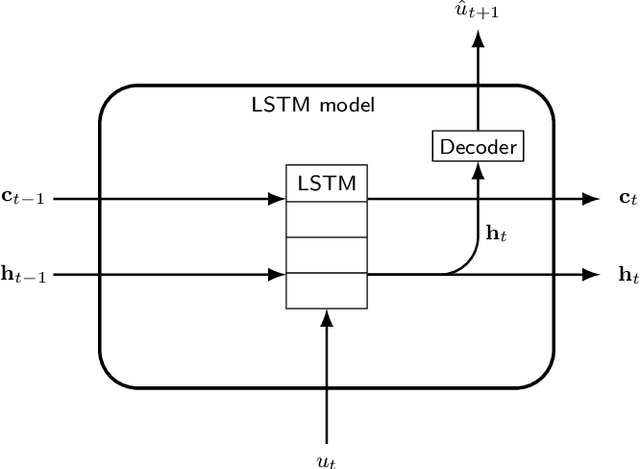
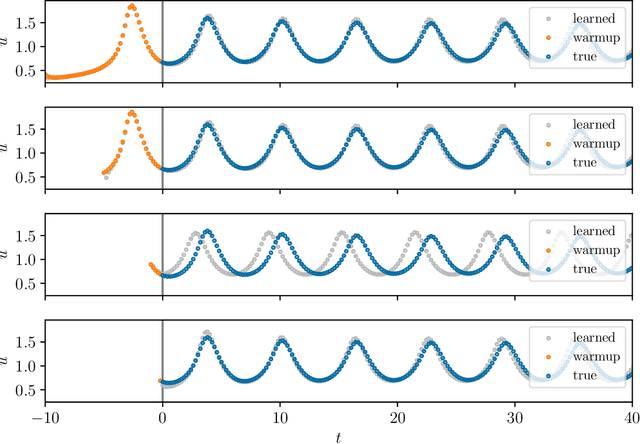
We present an approach, based on learning an intrinsic data manifold, for the initialization of the internal state values of LSTM recurrent neural networks, ensuring consistency with the initial observed input data. Exploiting the generalized synchronization concept, we argue that the converged, "mature" internal states constitute a function on this learned manifold. The dimension of this manifold then dictates the length of observed input time series data required for consistent initialization. We illustrate our approach through a partially observed chemical model system, where initializing the internal LSTM states in this fashion yields visibly improved performance. Finally, we show that learning this data manifold enables the transformation of partially observed dynamics into fully observed ones, facilitating alternative identification paths for nonlinear dynamical systems.

Learning emergent PDEs in a learned emergent space

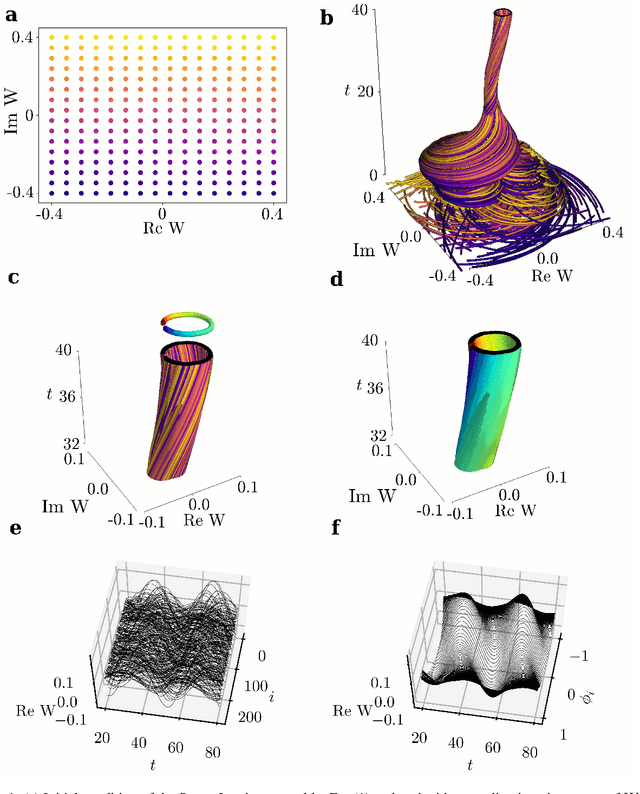
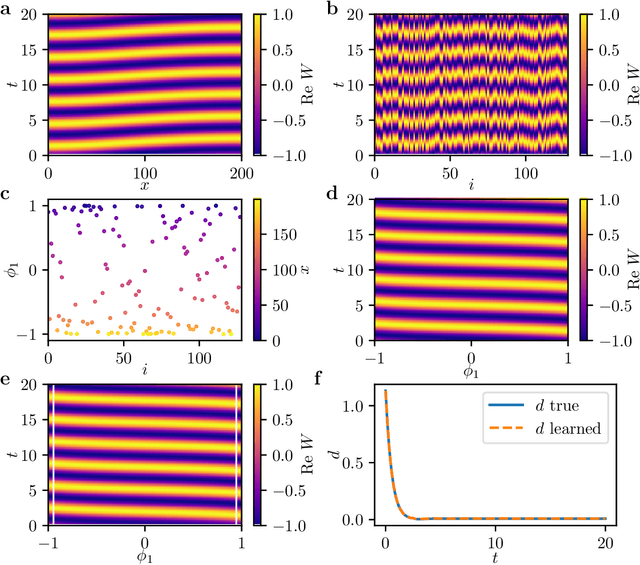
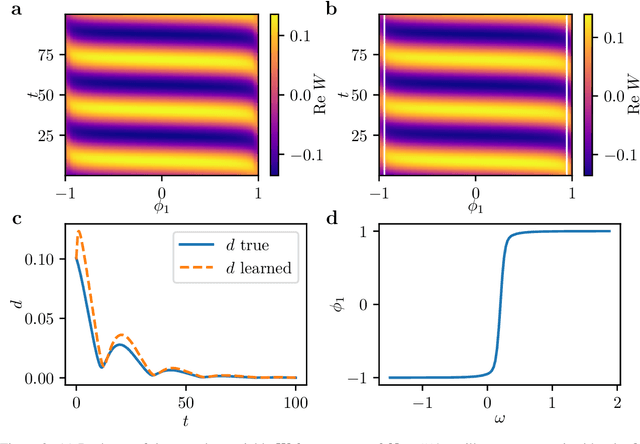
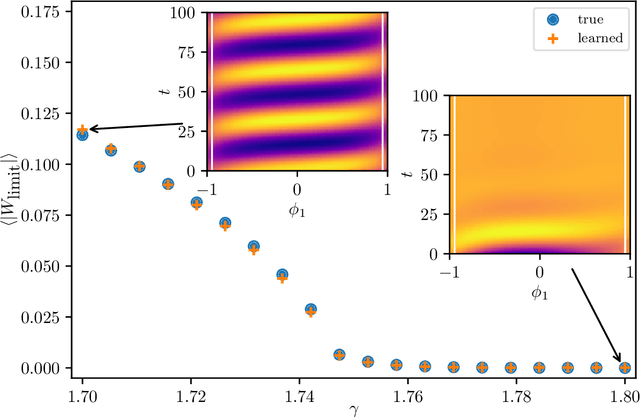
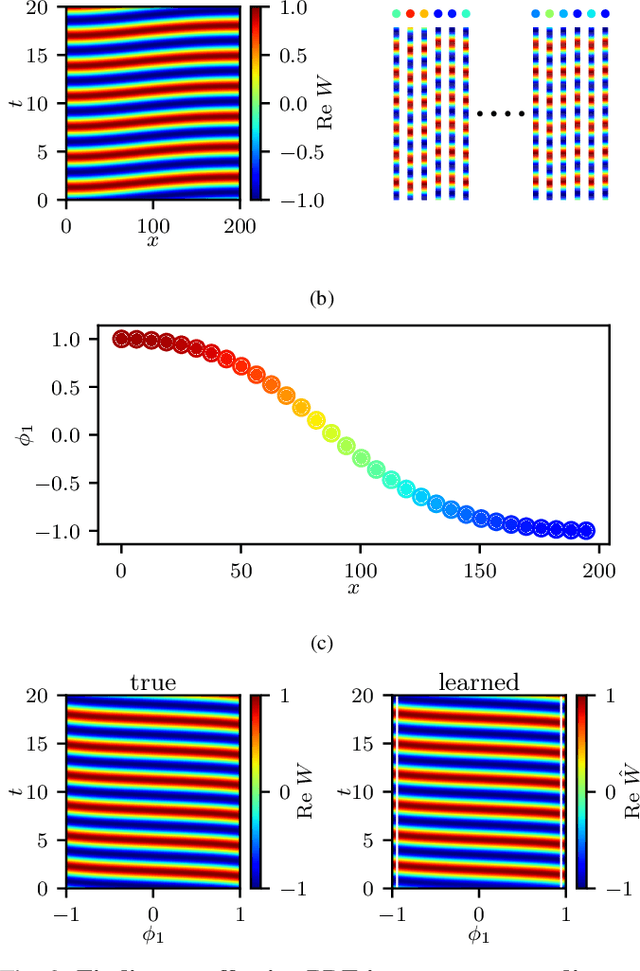
We extract data-driven, intrinsic spatial coordinates from observations of the dynamics of large systems of coupled heterogeneous agents. These coordinates then serve as an emergent space in which to learn predictive models in the form of partial differential equations (PDEs) for the collective description of the coupled-agent system. They play the role of the independent spatial variables in this PDE (as opposed to the dependent, possibly also data-driven, state variables). This leads to an alternative description of the dynamics, local in these emergent coordinates, thus facilitating an alternative modeling path for complex coupled-agent systems. We illustrate this approach on a system where each agent is a limit cycle oscillator (a so-called Stuart-Landau oscillator); the agents are heterogeneous (they each have a different intrinsic frequency $\omega$) and are coupled through the ensemble average of their respective variables. After fast initial transients, we show that the collective dynamics on a slow manifold can be approximated through a learned model based on local "spatial" partial derivatives in the emergent coordinates. The model is then used for prediction in time, as well as to capture collective bifurcations when system parameters vary. The proposed approach thus integrates the automatic, data-driven extraction of emergent space coordinates parametrizing the agent dynamics, with machine-learning assisted identification of an "emergent PDE" description of the dynamics in this parametrization.

Coarse-grained and emergent distributed parameter systems from data

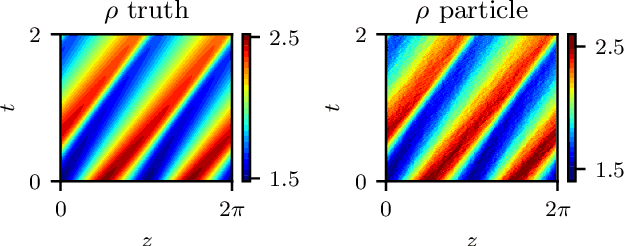
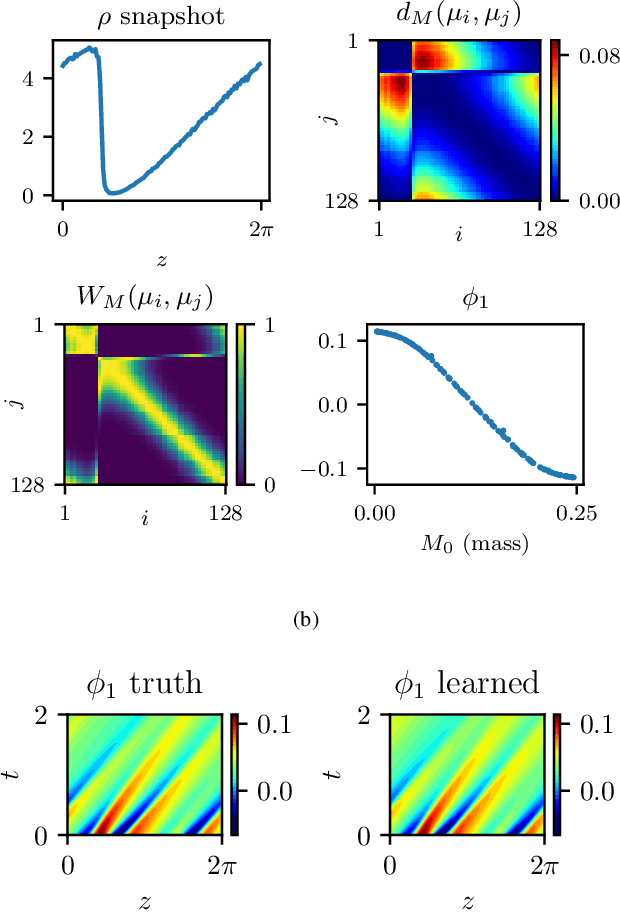
We explore the derivation of distributed parameter system evolution laws (and in particular, partial differential operators and associated partial differential equations, PDEs) from spatiotemporal data. This is, of course, a classical identification problem; our focus here is on the use of manifold learning techniques (and, in particular, variations of Diffusion Maps) in conjunction with neural network learning algorithms that allow us to attempt this task when the dependent variables, and even the independent variables of the PDE are not known a priori and must be themselves derived from the data. The similarity measure used in Diffusion Maps for dependent coarse variable detection involves distances between local particle distribution observations; for independent variable detection we use distances between local short-time dynamics. We demonstrate each approach through an illustrative established PDE example. Such variable-free, emergent space identification algorithms connect naturally with equation-free multiscale computation tools.

NeurIPS 2019 Disentanglement Challenge: Improved Disentanglement through Learned Aggregation of Convolutional Feature Maps

This report to our stage 2 submission to the NeurIPS 2019 disentanglement challenge presents a simple image preprocessing method for learning disentangled latent factors. We propose to train a variational autoencoder on regionally aggregated feature maps obtained from networks pretrained on the ImageNet database, utilizing the implicit inductive bias contained in those features for disentanglement. This bias can be further enhanced by explicitly fine-tuning the feature maps on auxiliary tasks useful for the challenge, such as angle, position estimation, or color classification. Our approach achieved the 2nd place in stage 2 of the challenge. Code is available at https://github.com/mseitzer/neurips2019-disentanglement-challenge.

The Effect of Data Augmentation on Classification of Atrial Fibrillation in Short Single-Lead ECG Signals Using Deep Neural Networks

Cardiovascular diseases are the most common cause of mortality worldwide. Detection of atrial fibrillation (AF) in the asymptomatic stage can help prevent strokes. It also improves clinical decision making through the delivery of suitable treatment such as, anticoagulant therapy, in a timely manner. The clinical significance of such early detection of AF in electrocardiogram (ECG) signals has inspired numerous studies in recent years, of which many aim to solve this task by leveraging machine learning algorithms. ECG datasets containing AF samples, however, usually suffer from severe class imbalance, which if unaccounted for, affects the performance of classification algorithms. Data augmentation is a popular solution to tackle this problem. In this study, we investigate the impact of various data augmentation algorithms, e.g., oversampling, Gaussian Mixture Models (GMMs) and Generative Adversarial Networks (GANs), on solving the class imbalance problem. These algorithms are quantitatively and qualitatively evaluated, compared and discussed in detail. The results show that deep learning-based AF signal classification methods benefit more from data augmentation using GANs and GMMs, than oversampling. Furthermore, the GAN results in circa $3\%$ better AF classification accuracy in average while performing comparably to the GMM in terms of f1-score.