EarthView: A Large Scale Remote Sensing Dataset for Self-Supervision

This paper presents EarthView, a comprehensive dataset specifically designed for self-supervision on remote sensing data, intended to enhance deep learning applications on Earth monitoring tasks. The dataset spans 15 tera pixels of global remote-sensing data, combining imagery from a diverse range of sources, including NEON, Sentinel, and a novel release of 1m spatial resolution data from Satellogic. Our dataset provides a wide spectrum of image data with varying resolutions, harnessed from different sensors and organized coherently into an accessible HuggingFace dataset in parquet format. This data spans five years, from 2017 to 2022. Accompanying the dataset, we introduce EarthMAE, a tailored Masked Autoencoder, developed to tackle the distinct challenges of remote sensing data. Trained in a self-supervised fashion, EarthMAE effectively processes different data modalities such as hyperspectral, multispectral, topographical data, segmentation maps, and temporal structure. This model helps us show that pre-training on Satellogic data improves performance on downstream tasks. While there is still a gap to fill in MAE for heterogeneous data, we regard this innovative combination of an expansive, diverse dataset and a versatile model adapted for self-supervised learning as a stride forward in deep learning for Earth monitoring.

Black and Gray Box Learning of Amplitude Equations: Application to Phase Field Systems

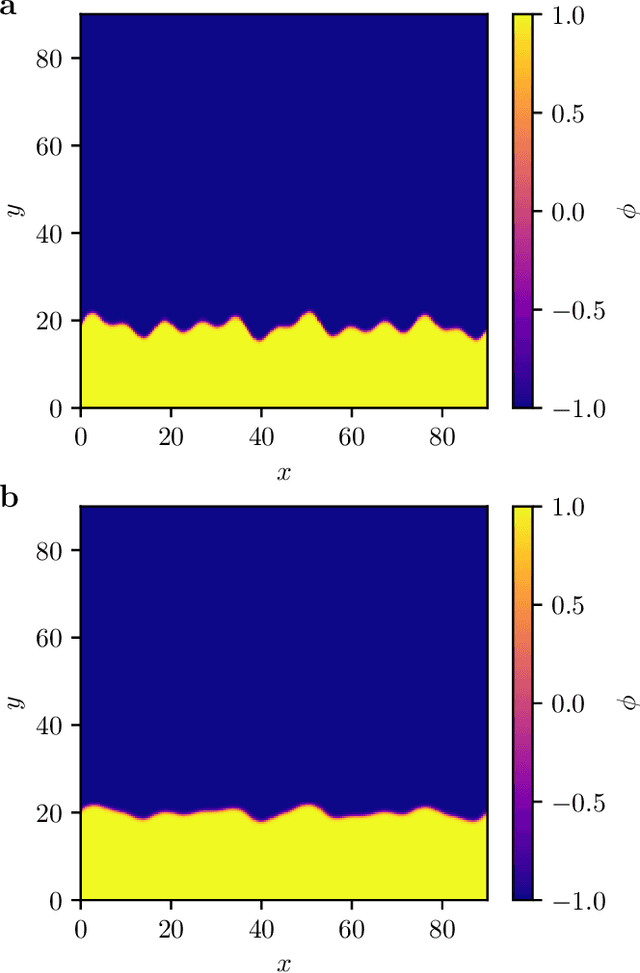
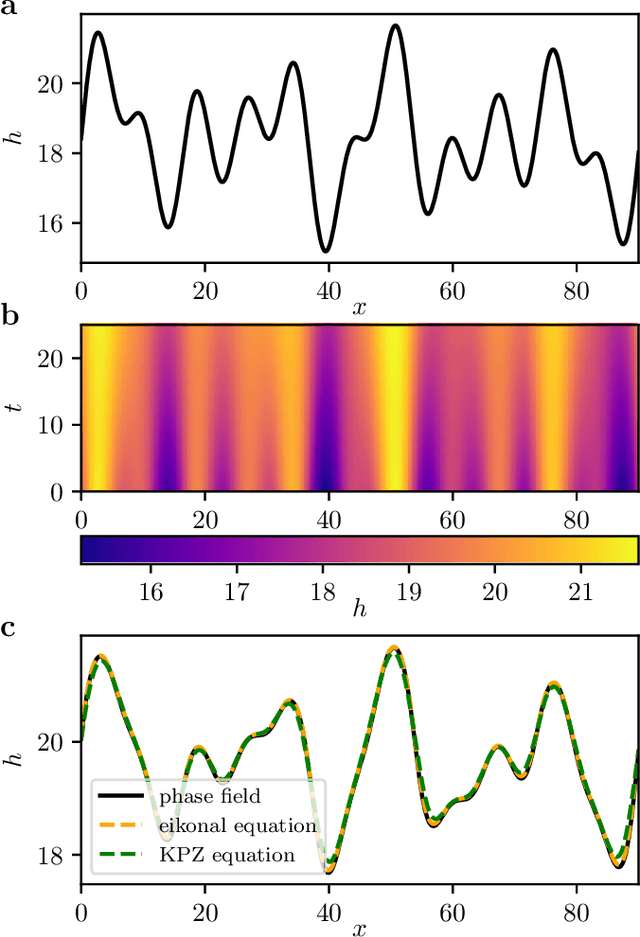
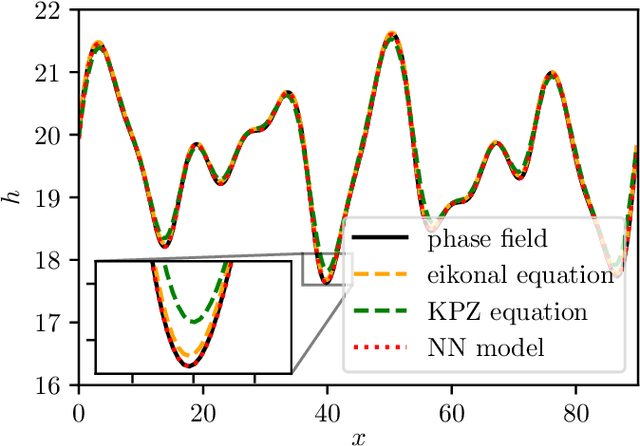
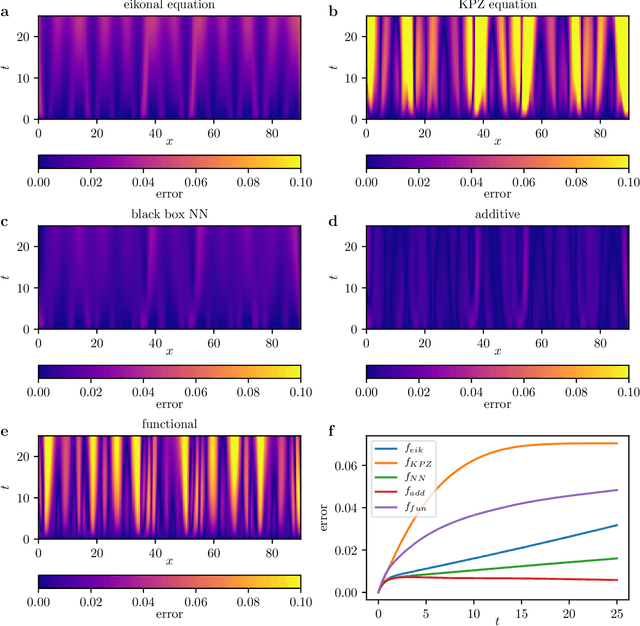
We present a data-driven approach to learning surrogate models for amplitude equations, and illustrate its application to interfacial dynamics of phase field systems. In particular, we demonstrate learning effective partial differential equations describing the evolution of phase field interfaces from full phase field data. We illustrate this on a model phase field system, where analytical approximate equations for the dynamics of the phase field interface (a higher order eikonal equation and its approximation, the Kardar-Parisi-Zhang (KPZ) equation) are known. For this system, we discuss data-driven approaches for the identification of equations that accurately describe the front interface dynamics. When the analytical approximate models mentioned above become inaccurate, as we move beyond the region of validity of the underlying assumptions, the data-driven equations outperform them. In these regimes, going beyond black-box identification, we explore different approaches to learn data-driven corrections to the analytically approximate models, leading to effective gray box partial differential equations.