Blas Echebarria
Black and Gray Box Learning of Amplitude Equations: Application to Phase Field Systems
Jul 08, 2022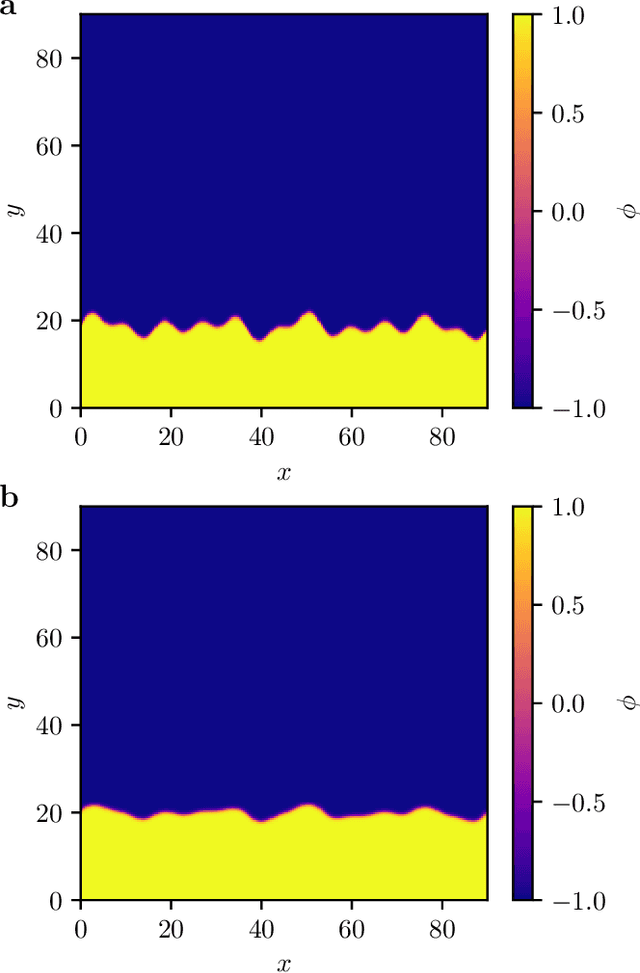
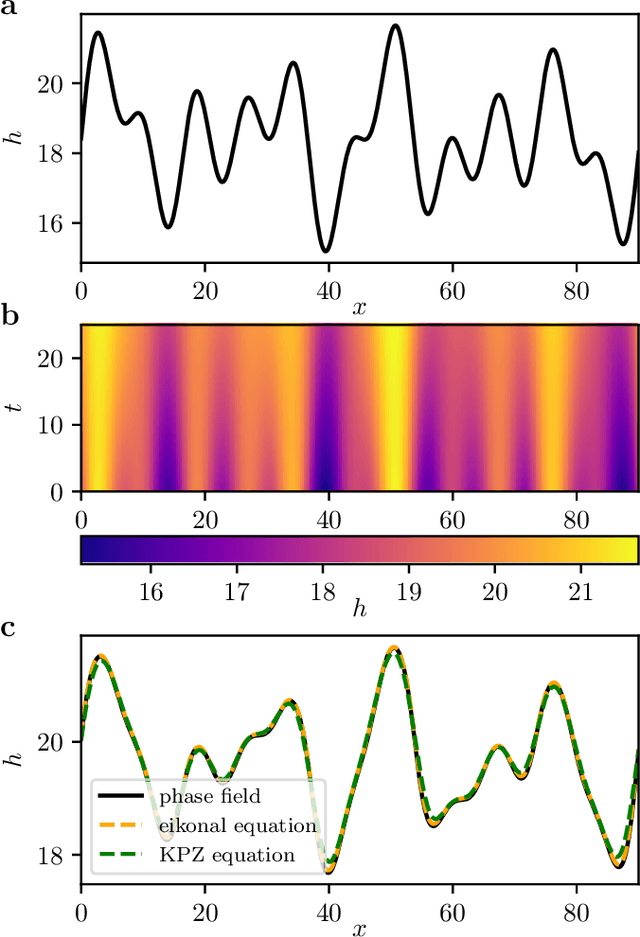
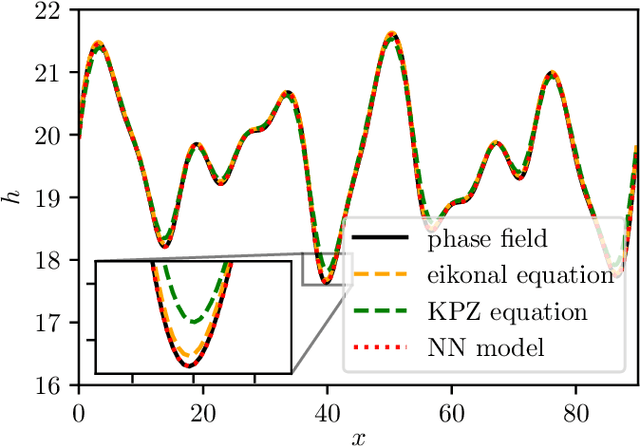
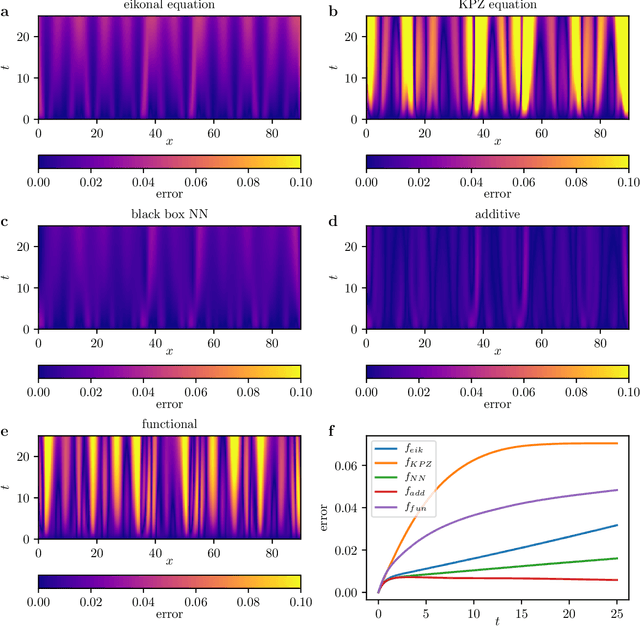
Abstract:We present a data-driven approach to learning surrogate models for amplitude equations, and illustrate its application to interfacial dynamics of phase field systems. In particular, we demonstrate learning effective partial differential equations describing the evolution of phase field interfaces from full phase field data. We illustrate this on a model phase field system, where analytical approximate equations for the dynamics of the phase field interface (a higher order eikonal equation and its approximation, the Kardar-Parisi-Zhang (KPZ) equation) are known. For this system, we discuss data-driven approaches for the identification of equations that accurately describe the front interface dynamics. When the analytical approximate models mentioned above become inaccurate, as we move beyond the region of validity of the underlying assumptions, the data-driven equations outperform them. In these regimes, going beyond black-box identification, we explore different approaches to learn data-driven corrections to the analytically approximate models, leading to effective gray box partial differential equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge