Some of the variables, some of the parameters, some of the times, with some physics known: Identification with partial information

Experimental data is often comprised of variables measured independently, at different sampling rates (non-uniform ${\Delta}$t between successive measurements); and at a specific time point only a subset of all variables may be sampled. Approaches to identifying dynamical systems from such data typically use interpolation, imputation or subsampling to reorganize or modify the training data $\textit{prior}$ to learning. Partial physical knowledge may also be available $\textit{a priori}$ (accurately or approximately), and data-driven techniques can complement this knowledge. Here we exploit neural network architectures based on numerical integration methods and $\textit{a priori}$ physical knowledge to identify the right-hand side of the underlying governing differential equations. Iterates of such neural-network models allow for learning from data sampled at arbitrary time points $\textit{without}$ data modification. Importantly, we integrate the network with available partial physical knowledge in "physics informed gray-boxes"; this enables learning unknown kinetic rates or microbial growth functions while simultaneously estimating experimental parameters.

Initializing LSTM internal states via manifold learning

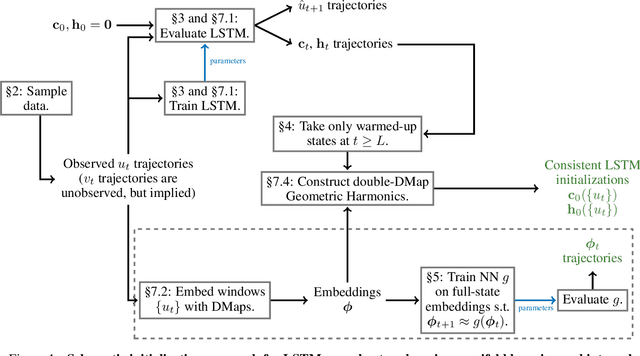
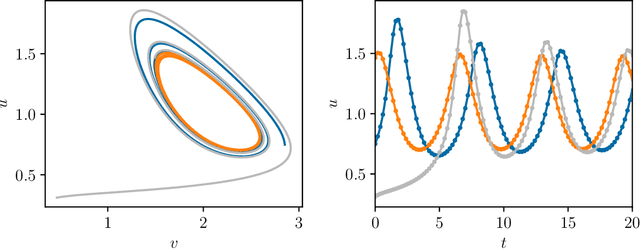
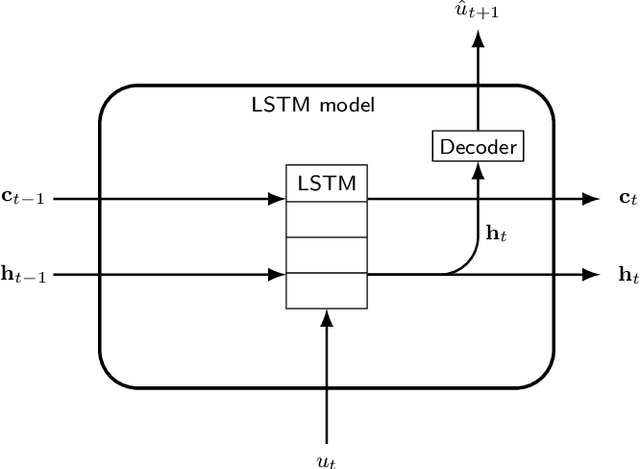
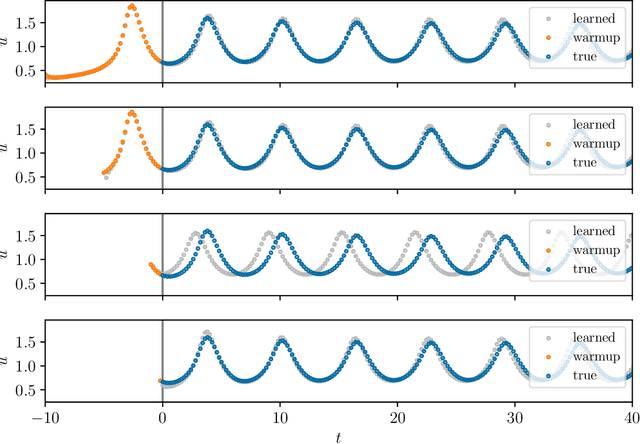
We present an approach, based on learning an intrinsic data manifold, for the initialization of the internal state values of LSTM recurrent neural networks, ensuring consistency with the initial observed input data. Exploiting the generalized synchronization concept, we argue that the converged, "mature" internal states constitute a function on this learned manifold. The dimension of this manifold then dictates the length of observed input time series data required for consistent initialization. We illustrate our approach through a partially observed chemical model system, where initializing the internal LSTM states in this fashion yields visibly improved performance. Finally, we show that learning this data manifold enables the transformation of partially observed dynamics into fully observed ones, facilitating alternative identification paths for nonlinear dynamical systems.