Thomas Thiem
Learning emergent PDEs in a learned emergent space
Dec 23, 2020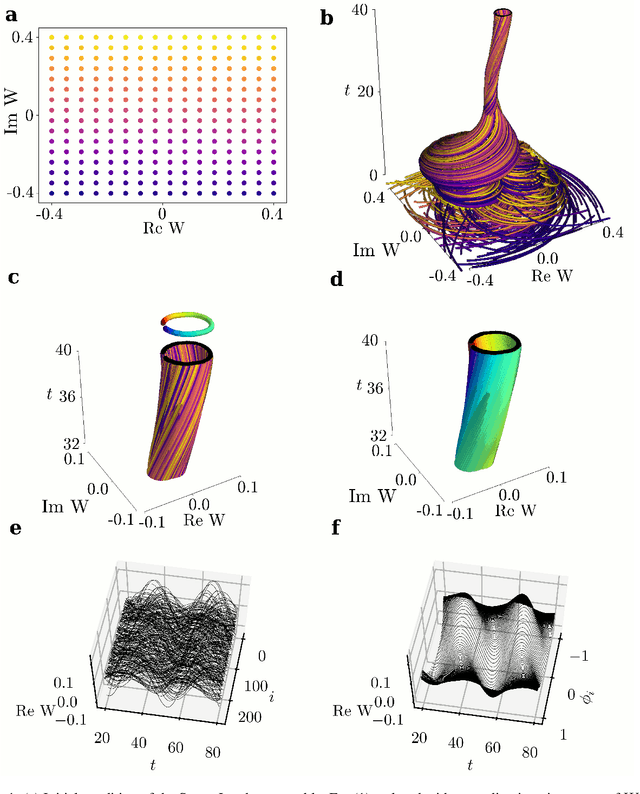
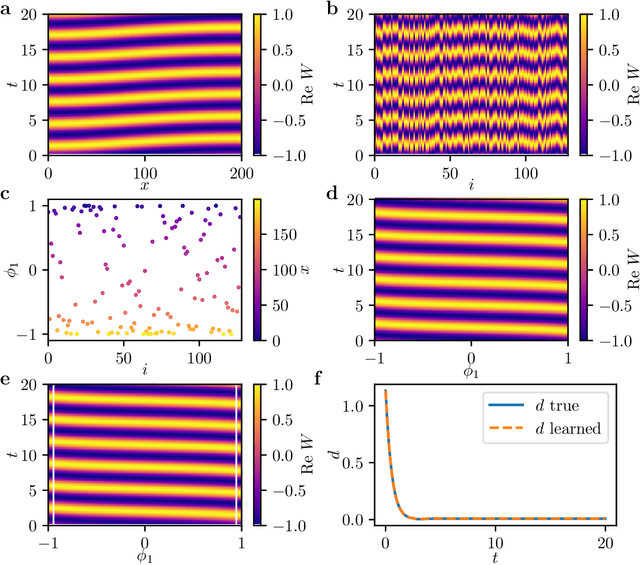
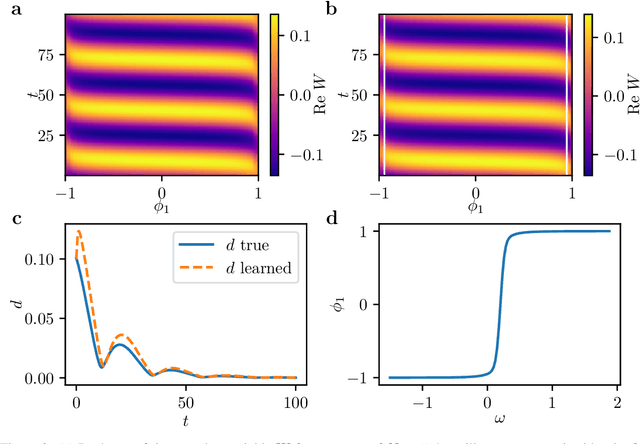
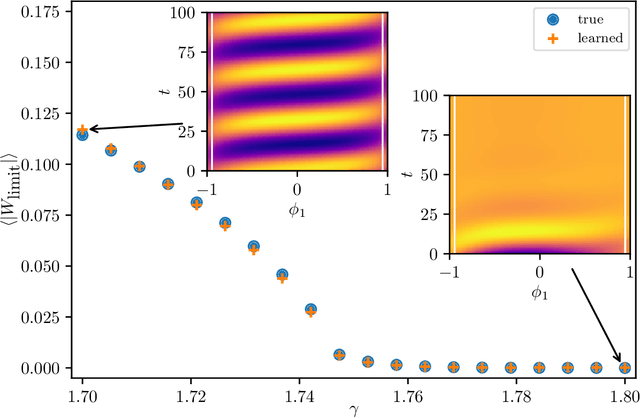
Abstract:We extract data-driven, intrinsic spatial coordinates from observations of the dynamics of large systems of coupled heterogeneous agents. These coordinates then serve as an emergent space in which to learn predictive models in the form of partial differential equations (PDEs) for the collective description of the coupled-agent system. They play the role of the independent spatial variables in this PDE (as opposed to the dependent, possibly also data-driven, state variables). This leads to an alternative description of the dynamics, local in these emergent coordinates, thus facilitating an alternative modeling path for complex coupled-agent systems. We illustrate this approach on a system where each agent is a limit cycle oscillator (a so-called Stuart-Landau oscillator); the agents are heterogeneous (they each have a different intrinsic frequency $\omega$) and are coupled through the ensemble average of their respective variables. After fast initial transients, we show that the collective dynamics on a slow manifold can be approximated through a learned model based on local "spatial" partial derivatives in the emergent coordinates. The model is then used for prediction in time, as well as to capture collective bifurcations when system parameters vary. The proposed approach thus integrates the automatic, data-driven extraction of emergent space coordinates parametrizing the agent dynamics, with machine-learning assisted identification of an "emergent PDE" description of the dynamics in this parametrization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge