Parsimonious Physics-Informed Random Projection Neural Networks for Initial-Value Problems of ODEs and index-1 DAEs

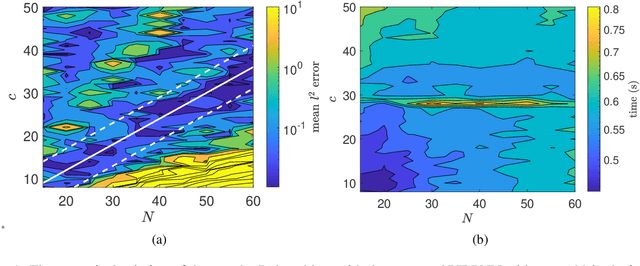
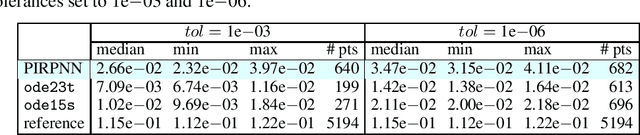
We address a physics-informed neural network based on the concept of random projections for the numerical solution of IVPs of nonlinear ODEs in linear-implicit form and index-1 DAEs, which may also arise from the spatial discretization of PDEs. The scheme has a single hidden layer with appropriately randomly parametrized Gaussian kernels and a linear output layer, while the internal weights are fixed to ones. The unknown weights between the hidden and output layer are computed by Newton's iterations, using the Moore-Penrose pseudoinverse for low to medium, and sparse QR decomposition with regularization for medium to large scale systems. To deal with stiffness and sharp gradients, we propose a variable step size scheme for adjusting the interval of integration and address a continuation method for providing good initial guesses for the Newton iterations. Based on previous works on random projections, we prove the approximation capability of the scheme for ODEs in the canonical form and index-1 DAEs in the semiexplicit form. The optimal bounds of the uniform distribution are parsimoniously chosen based on the bias-variance trade-off. The performance of the scheme is assessed through seven benchmark problems: four index-1 DAEs, the Robertson model, a model of five DAEs describing the motion of a bead, a model of six DAEs describing a power discharge control problem, the chemical Akzo Nobel problem and three stiff problems, the Belousov-Zhabotinsky, the Allen-Cahn PDE and the Kuramoto-Sivashinsky PDE. The efficiency of the scheme is compared with three solvers ode23t, ode23s, ode15s of the MATLAB ODE suite. Our results show that the proposed scheme outperforms the stiff solvers in several cases, especially in regimes where high stiffness or sharp gradients arise in terms of numerical accuracy, while the computational costs are for any practical purposes comparable.

Constructing coarse-scale bifurcation diagrams from spatio-temporal observations of microscopic simulations: A parsimonious machine learning approach

We address a three-tier data-driven approach to solve the inverse problem in complex systems modelling from spatio-temporal data produced by microscopic simulators using machine learning. In the first step, we exploit manifold learning and in particular parsimonious Diffusion Maps using leave-one-out cross-validation (LOOCV) to both identify the intrinsic dimension of the manifold where the emergent dynamics evolve and for feature selection over the parametric space. In the second step, based on the selected features, we learn the right-hand-side of the effective partial differential equations (PDEs) using two machine learning schemes, namely shallow Feedforward Neural Networks (FNNs) with two hidden layers and single-layer Random Projection Networks(RPNNs) which basis functions are constructed using an appropriate random sampling approach. Finally, based on the learned black-box PDE model, we construct the corresponding bifurcation diagram, thus exploiting the numerical bifurcation analysis toolkit. For our illustrations, we implemented the proposed method to construct the one-parameter bifurcation diagram of the 1D FitzHugh-Nagumo PDEs from data generated by $D1Q3$ Lattice Boltzmann simulations. The proposed method was quite effective in terms of numerical accuracy regarding the construction of the coarse-scale bifurcation diagram. Furthermore, the proposed RPNN scheme was $\sim$ 20 to 30 times less costly regarding the training phase than the traditional shallow FNNs, thus arising as a promising alternative to deep learning for solving the inverse problem for high-dimensional PDEs.

Numerical Solution of Stiff Ordinary Differential Equations with Random Projection Neural Networks

We propose a numerical scheme based on Random Projection Neural Networks (RPNN) for the solution of Ordinary Differential Equations (ODEs) with a focus on stiff problems. In particular, we use an Extreme Learning Machine, a single-hidden layer Feedforward Neural Network with Radial Basis Functions which widths are uniformly distributed random variables, while the values of the weights between the input and the hidden layer are set equal to one. The numerical solution is obtained by constructing a system of nonlinear algebraic equations, which is solved with respect to the output weights using the Gauss-Newton method. For our illustrations, we apply the proposed machine learning approach to solve two benchmark stiff problems, namely the Rober and the van der Pol ones (the latter with large values of the stiffness parameter), and we perform a comparison with well-established methods such as the adaptive Runge-Kutta method based on the Dormand-Prince pair, and a variable-step variable-order multistep solver based on numerical differentiation formulas, as implemented in the \texttt{ode45} and \texttt{ode15s} MATLAB functions, respectively. We show that our proposed scheme yields good numerical approximation accuracy without being affected by the stiffness, thus outperforming in same cases the \texttt{ode45} and \texttt{ode15s} functions. Importantly, upon training using a fixed number of collocation points, the proposed scheme approximates the solution in the whole domain in contrast to the classical time integration methods.

Construction of embedded fMRI resting state functional connectivity networks using manifold learning

We construct embedded functional connectivity networks (FCN) from benchmark resting-state functional magnetic resonance imaging (rsfMRI) data acquired from patients with schizophrenia and healthy controls based on linear and nonlinear manifold learning algorithms, namely, Multidimensional Scaling (MDS), Isometric Feature Mapping (ISOMAP) and Diffusion Maps. Furthermore, based on key global graph-theoretical properties of the embedded FCN, we compare their classification potential using machine learning techniques. We also assess the performance of two metrics that are widely used for the construction of FCN from fMRI, namely the Euclidean distance and the lagged cross-correlation metric. We show that the FCN constructed with Diffusion Maps and the lagged cross-correlation metric outperform the other combinations.