Parsimonious Physics-Informed Random Projection Neural Networks for Initial-Value Problems of ODEs and index-1 DAEs
Paper and Code
Mar 11, 2022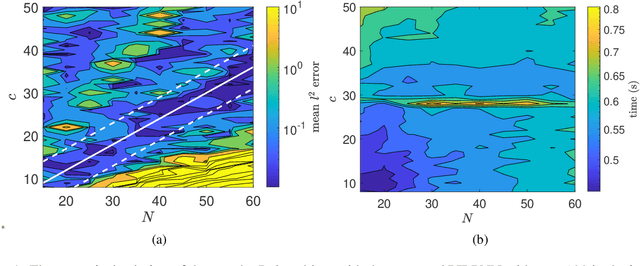

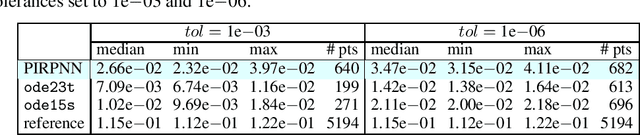

We address a physics-informed neural network based on the concept of random projections for the numerical solution of IVPs of nonlinear ODEs in linear-implicit form and index-1 DAEs, which may also arise from the spatial discretization of PDEs. The scheme has a single hidden layer with appropriately randomly parametrized Gaussian kernels and a linear output layer, while the internal weights are fixed to ones. The unknown weights between the hidden and output layer are computed by Newton's iterations, using the Moore-Penrose pseudoinverse for low to medium, and sparse QR decomposition with regularization for medium to large scale systems. To deal with stiffness and sharp gradients, we propose a variable step size scheme for adjusting the interval of integration and address a continuation method for providing good initial guesses for the Newton iterations. Based on previous works on random projections, we prove the approximation capability of the scheme for ODEs in the canonical form and index-1 DAEs in the semiexplicit form. The optimal bounds of the uniform distribution are parsimoniously chosen based on the bias-variance trade-off. The performance of the scheme is assessed through seven benchmark problems: four index-1 DAEs, the Robertson model, a model of five DAEs describing the motion of a bead, a model of six DAEs describing a power discharge control problem, the chemical Akzo Nobel problem and three stiff problems, the Belousov-Zhabotinsky, the Allen-Cahn PDE and the Kuramoto-Sivashinsky PDE. The efficiency of the scheme is compared with three solvers ode23t, ode23s, ode15s of the MATLAB ODE suite. Our results show that the proposed scheme outperforms the stiff solvers in several cases, especially in regimes where high stiffness or sharp gradients arise in terms of numerical accuracy, while the computational costs are for any practical purposes comparable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge