Learning Effective SDEs from Brownian Dynamics Simulations of Colloidal Particles

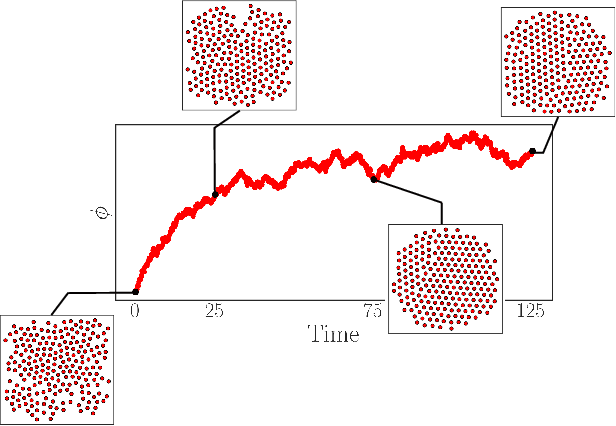
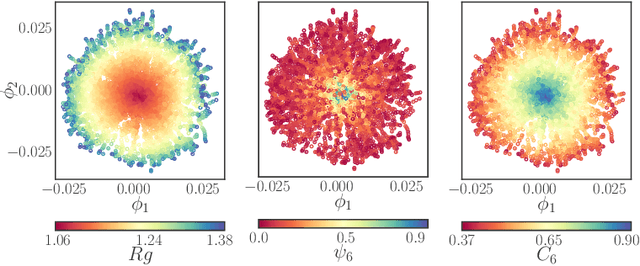
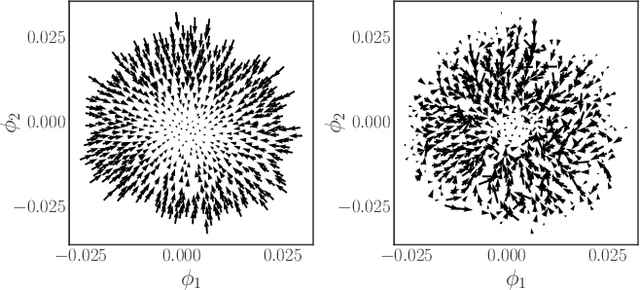
We construct a reduced, data-driven, parameter dependent effective Stochastic Differential Equation (eSDE) for electric-field mediated colloidal crystallization using data obtained from Brownian Dynamics Simulations. We use Diffusion Maps (a manifold learning algorithm) to identify a set of useful latent observables. In this latent space we identify an eSDE using a deep learning architecture inspired by numerical stochastic integrators and compare it with the traditional Kramers-Moyal expansion estimation. We show that the obtained variables and the learned dynamics accurately encode the physics of the Brownian Dynamic Simulations. We further illustrate that our reduced model captures the dynamics of corresponding experimental data. Our dimension reduction/reduced model identification approach can be easily ported to a broad class of particle systems dynamics experiments/models.

Efficient Navigation of Colloidal Robots in an Unknown Environment via Deep Reinforcement Learning

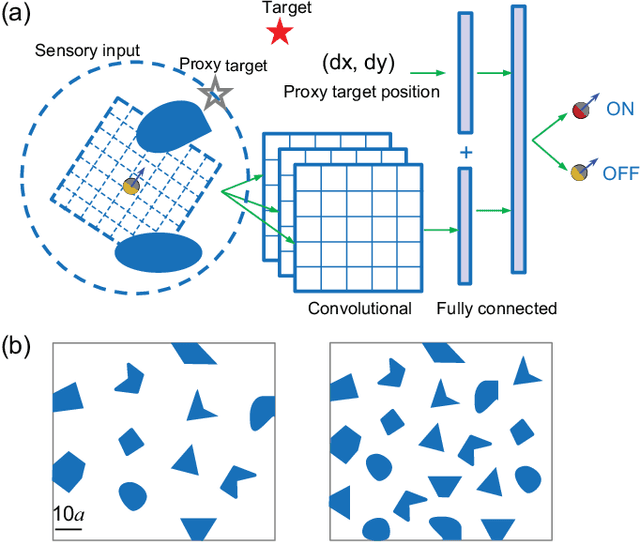
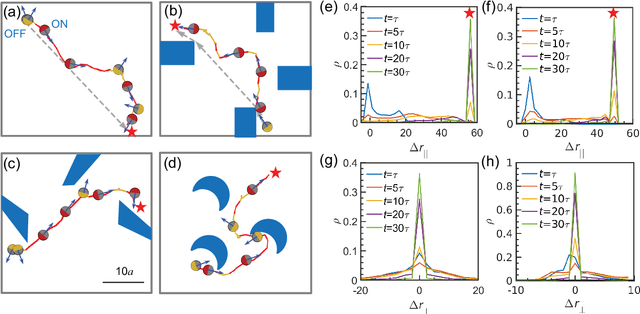
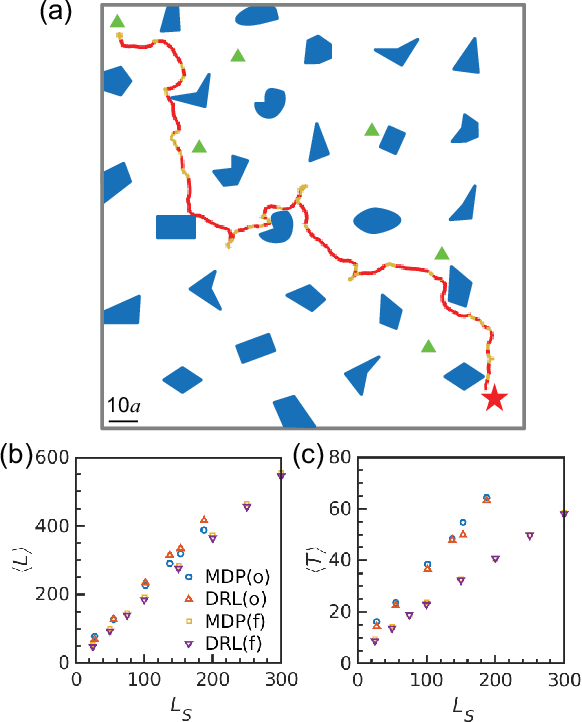
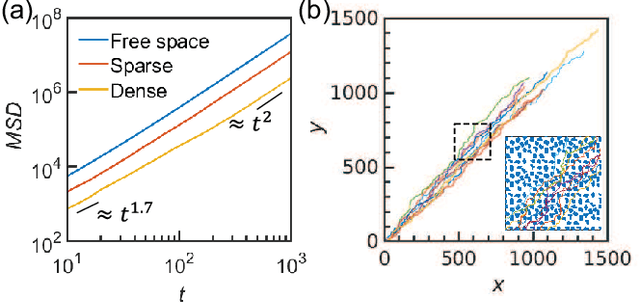
Equipping active colloidal robots with intelligence such that they can efficiently navigate in unknown complex environments could dramatically impact their use in emerging applications like precision surgery and targeted drug delivery. Here we develop a model-free deep reinforcement learning that can train colloidal robots to learn effective navigation strategies in unknown environments with random obstacles. We show that trained robot agents learn to make navigation decisions regarding both obstacle avoidance and travel time minimization, based solely on local sensory inputs without prior knowledge of the global environment. Such agents with biologically inspired mechanisms can acquire competitive navigation capabilities in large-scale, complex environments containing obstacles of diverse shapes, sizes, and configurations. This study illustrates the potential of artificial intelligence in engineering active colloidal systems for future applications and constructing complex active systems with visual and learning capability.