Ioannis G. Kevekidis
Learning Effective SDEs from Brownian Dynamics Simulations of Colloidal Particles
Apr 30, 2022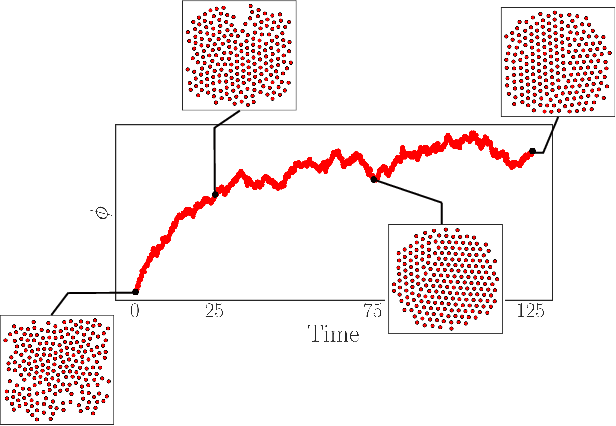

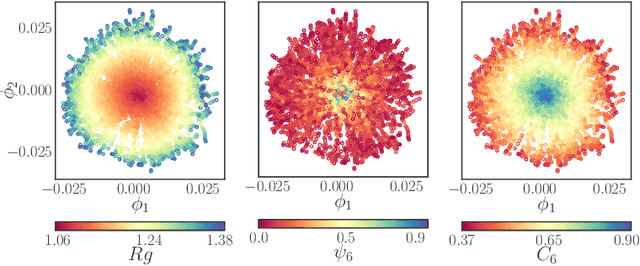
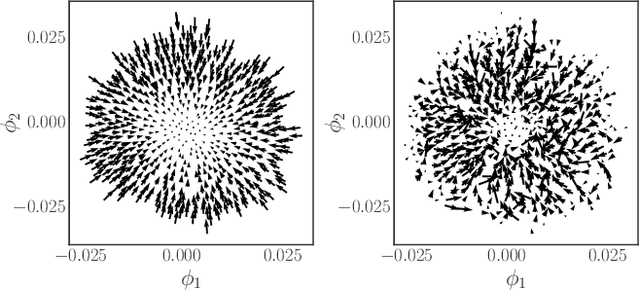
Abstract:We construct a reduced, data-driven, parameter dependent effective Stochastic Differential Equation (eSDE) for electric-field mediated colloidal crystallization using data obtained from Brownian Dynamics Simulations. We use Diffusion Maps (a manifold learning algorithm) to identify a set of useful latent observables. In this latent space we identify an eSDE using a deep learning architecture inspired by numerical stochastic integrators and compare it with the traditional Kramers-Moyal expansion estimation. We show that the obtained variables and the learned dynamics accurately encode the physics of the Brownian Dynamic Simulations. We further illustrate that our reduced model captures the dynamics of corresponding experimental data. Our dimension reduction/reduced model identification approach can be easily ported to a broad class of particle systems dynamics experiments/models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge